쿼터니언 이해하기

https://www.3dgep.com/understanding-quaternions/
--------------------------------------------------------------------------------
이 자료에서 나는 이해하기 쉬운 방법으로 쿼터니언의 개념을 설명할 것이다. 나는 너가 어떻게 쿼터니언을 시각화하고 쿼터니언에 적용될 수 있는 다른 연산들을 어떻게 설명할지를 설명할 것이다. 나는 또한 행렬, 오일러 각, 쿼터니언들의 적용을 비교할 것이고 언제 오일러 각 또는 행렬들 대신에 쿼터니언을 사용하기를 원하는지를 설명할 것이다. 또는 너가 언제 쓰지 말아야 할지를.

Contents
1. 도입
2. 복소수
  2.1 복소수 덧셈과 뺄셈
  2.2 복소수의 스칼라곱
  2.3 복소수의 곱
  2.4 복소수의 제곱
  2.5 켤레복소수
  2.6 복소수의 절대값
  2.7 두 복소수의 몫
3. i의 지수승
4. 복소평면
  4.1 Rotors
5. 사원소
  5.1 순서쌍으로서의 쿼터니언
  5.2 쿼터니언 더하기와 뺄셈
  5.3 쿼터니언 곱
  5.4 실수 쿼터니언
  5.5 쿼터니언의 스칼라곱
  5.6 Pure 쿼터니언
  5.7 쿼터니언의 Additive Form
  5.8 단위 쿼터니언
  5.9 쿼터니언의 이진 형태
  5.10 켤레 쿼터니언
  5.11 쿼터니언 Norm
  5.12 쿼터니언 정규화
  5.13 쿼터니언 역
  5.14 쿼터니언 내적
6. 회전
7. 쿼터니언 Interpolation
  7.1 SLERP
    7.1.1 Quaternion Difference
    7.1.2 Quaternion Exponentation
    7.1.3 Fractional difference of Quaternions
    7.1.4 Considerations
   7.2 SQUAD
8. Conclusion
9. Download the Demo
10. Reference

! 너는 그냥 45분 만에 쿼터니언을 이해할 수 없다. 이 자료는 매우 수학적이며, 약한 심장을 가진 사람을 위한 자료가 아니다.

Introduction
컴퓨터 그래픽스에서, 공간에서의 위치(평행이동)와 공간에서의 방향(회전)을 표현하기 위해 transformation 행렬을 사용한다. 선택적으로, 단일의 transformation 행렬은 또한 scale 또는 한 오브젝트의 "shear"을 표현하기 위해 사용될 수 있다. 우리는 이 변홚 ㅐㅇ렬을 "기저 공간"으로 생각할 수 있다. 그 기저공간에서, 만약 너가 한 벡터 또는 한 점을 (또는 심지어 다른 행렬을) 한 transformation matrix로 곱한다면, 너는 그 벡터, 점 또는 행렬을 그 행렬에 의해 표현되는 공간으로 "변환한다".

이 자료에서, 나는 변환 행렬의 세부사항을 이야기하지 않을 것이다. 변환 행렬의 세부 묘사에 대해서 너는 나의 이전 자료 Matrices를 참고할 수 있다.

이 자료에서, 나는 쿼터니언을 사용하여 공간에서 한 오브젝트의 방향(회전)을 묘사하는 다른 방법을 이야기하고 싶다.

쿼터니언의 개념은 아일랜드 수학자 Sir William Rowan Hamilton이 1843년 아일랜드 더블린에서 1843년 10월 16일 월요일에  만들었다. Hamilton은 그의 아내와 Royal Irish Academy에 가는 길이 였고, 그가 Brougham 다리에서 Royal Canal위를 지날 때, 그는 그가 즉시 다리위의 돌에 새겨넣은 극적인 깨달음을 얻었다.



Complex Numbers
우리가 쿼터니언을 완전 이해하기전에, 우리는 처음에 그것들이 어디에서 왔는지 이해해야만 한다. 쿼터니언의 뿌리는 복소수 체계의 개념을 기반으로 한다.

잘 알려진 숫자들의 집합(자연수, 정수, 실수, 그리고 유리수)외에도, 복소수 체계는 허수라고 불려지는 숫자들의 새로운 집합을 도입한다. 허수는 다음과 같은 해가 없는 어떤 방정식을 해결하기 위해 발명되었다.

  x^2 + 1 = 0

이 문장을 해결하기 위해서, 우리는 우리가 알기에 불가능한 x^2 = -1이라는 것을 명시해야만 한다. 왜냐하면 어떤 수의 제곱 (양수 또는 음수) 항상 양수이기 때문이다.

수학자들은 일반적으로 한 식이 해가 없다는 것을 받아들일 수 없었다. 그래서 허수라는 새로운 용어가 발명되었다. 이것으로 그러한 방정식을 해결하기 위해 사용될 수 있다.

허수는 이러한 형태를 갖는다:

  i^2 = -1

이 용어를 실제로 이해하려고 하지마라. 그것이 존재하는지에 대한 논리적인 이유가 없으니까. 우리는 그냥 i는 제곱해서 -1이 되는 어떤 것이라고 받아들여야 한다.

허수의 집합은 로 나타내어 질 수 있다.

복소수들의 집합은 (기호로 나타내어지는) 실수와 허수의 합이고 다음의 형태를 갖는다:



그것은 또한 모든 복소수들은 b = 0인 복소수이고, 모든 허수들은 a = 0인 복소수라고 명시될 수 있다.

Adding and Subtracting Complex Numbers
Multiply a Complex Number by a Scalar
Product of Complex Numbers
Square of Complex Numbers
Complex Conjugate
Absolute Value of a Complex Number
Quotient of Two Complex Numbers
Powers of i
The Complex Plane

Rotors
우리는 또한 복소 평면에서 이러한 형태의 복소수를 정의하여 임의의 회전들을 수행할 수 있다:



어떤 복소수를 rotor q로 곱하는 것은 일반적인 공식을 만들어 낸다:



그리고 이것은 행렬의 형태로 쓰여질 수 있다:


이것은 복소 평면에서 원점에 대해 시계 반대방향으로 임의의 점을 회전시키는 방법이다.

Quaternions
복소수 체계와 복소평면의 지식을 가지고, 우리는 i 외에도 두 개의 허수들을 우리의 수 체계에 더하여 이것을 3차원 공간으로 확장시킬 수 있다.

쿼터니언을 표현하는 일반 형태는



Hamilton의 유명한 표현에 따라:


그리고



너는 i,j,k사이의 관계가 어떤 카르테시안 벡터에 대한 외적 규칙과 유사하다는 것을 눈치 챘을지도 모른다.



Hamilton은 또한 i,j 그리고 k의 허수가 이러한 카르테시안 단위 벡터 i, j 그리고 k를 허수의 의 같은 특징을 가지고 나타내기 위해 사용될 수 있다는 것을 인지했었다. i^2 = j^2 = k^2 = -1이 되게 하면서.

위의 이미지는 카르테시안 단위 벡터 사이의 관계를 i, j, k로 시각화 한 것이다.

Quaternions as an Ordered Pair
우리는 또한 쿼터니언들을 하나의 순서쌍으로 표현할 수 있다.



여기에서 v는 그것의 각각의 components들로 나타내어질 수 있다:



이 표기법을 사용하여, 우리는 좀 더 쉽게 쿼터니언과 복소수 사이의 유사성을 보여줄 수 있다.

Adding and Subtracting Quaternions
쿼터니언은 복소수와 유사하게 더해지고 빼질 수 있다.



Quaternion Products
우리는 또한 두 쿼터니언들의 곱을 표현할 수 있다:



이것은 다른 쿼터니언을 만들어 낸다. 만약 우리가 이전 표현에 있는 허수 i, j, 그리고 k를 순서쌍으로 (또한 quaternion units(단위 쿼터니언)으로 알려진) 교체한다면,



그리고 원래의 식에서 [1,0] = 1로 함께 치환하는 것은 다음을 준다.



그리고 이 식을 순서쌍의 합으로 전개하는 것은 다음을 준다:



만약 우리가 단위 쿼터니언으로 곱하고, 공통 벡터요소를 추출한다면, 우리는 이 방정식을 이렇게 다시 쓸 수 있다:



이 방정식은 두 개의 순서쌍의 합을 준다. 그 첫 번째 순서쌍은  실수 쿼터니언이고 두 번째 순서쌍은 Pure quaternion이다. 이러한 두 순서쌍은 단일의 순서쌍을 합쳐질 수 있다:



그리고 만약 우리가 치환한다면,



우리는 얻는다:



그리고 이것이 쿼터니언 곱의 일반식이다.

A Real Quaternion
Real Quaternion은 vector항이 0인 쿼터니언이다:



그리고 두 실수 쿼터니언들의 곱은 다른 실수 쿼터니언이다:



이것은 허수항이 0을 포함하는 두 복소수의 곱과 유사하다.

Multiplying a Quaternion by a Scalar
우리는 또한 규칙을 따르는 스칼라곱을 할 수 있다:



우리는 쿼터니언에 Real Quaternion으로서 스칼라로 곱하기 위해 위에서 보여준 곱 또는 Real Quaternion을 사용하여 이것을 확인할 수 있다:



Pure Quaternions
Real Quatnions와 유사하게, Hamilton은 또한 0의 스칼라항을 가진 한 Quaternion으로서의 Pure Quaternion을 정의했다:



또는 그것의 component 부분에서 이렇게 쓰인다:



그리고 우리는 두 Pure quternion들의 곱을 취할 수 있다:



위의 쿼터니언 곱에 따라서.

Additive Form of a Quaternion
우리는 실수부와 Pure quaternion부의 덧셈으로 쿼터니언을 표현할 수 있다:



Unit Quaternion
임의의 벡터 v가 주어진다면, 우리는 이 벡터를 그것의 스칼라 크기와 그것의 방향으로 표현할 수 있다:



그리고 puer quternion의 정의와함께 이 정의를 합하는 것은 다음을 준다:



그리고 우리는 또한 0의 스칼라와 단위 벡터를 가진 단위 쿼터니언을 묘사할 수 있다:



Binary Form of a Quaternion
우리는 이제 단위 쿼터니언의 정의와 쿼터니언의 덧셈 형태를 합칠 수 있고, 우리는 복소수를 묘사하는데 사용된 표기법과 유사한 쿼터니언의 표현을 만들 수 있다:



이것은 복소수와 슈사한 쿼터니언을 표현하는 방법을 우리에게 준다:



Quaternion Conjugate
켤레 쿼터니언은 쿼터니언의 벡터 부분에 음수를 곱하여 연산될 수 있다.



그리고 그것의 켤레와 한 쿼터니언의 곱은 다음을 준다:



Quaternion Norm
너가 복소수의 norm의 정의를 회상한다면:



유사하게, 한 쿼터니언의 norm (또는 크기)는 다음과 같이 정의된다:



Quaternion Normalization
quaternion 크기의 정의와 함께, 우리는 쿼터니언을 표준화 시키기위해 그것을 사용할 수 있다. 쿼터니언은 그것을 |q|로 나누어서 표준화 되어진다:



한 예시로 이 쿼터니언을 표준화 해보자:



처음에, 우리는 그 쿼터니언의 크기(norm)을 연산해야만 한다:



그러고나서, 우리는 표준화된 쿼터니언을 계산하기 위해 그 쿼터니언을 쿼터니언의 크기로 나눠야 한다.



Quaternion Inverse
쿼터니언의 역은 q^-1로 표기된다. 한 쿼터니언의 역을 계산하기 위해서, 우리는 그 쿼터니언의 켤레를 취하고, 그것을 크기의 제곱으로 나누어준다:



이것을 보여주기 위해서, 우리는 역의 정의를 이용해 다음의 사실을 얻을 수 있다:



그리고 양 변에 그 쿼터니언의 켤레를 곱하는 것은 다음을 준다:



크기가 1인 다위 크기 쿼터니언에 대해서 우리는 다음과 같이 쓸 수 있다:



Quaternion Dot Product
벡터의 내적과 유사하게, 우리는 또한 대응하는 스칼라 부분과, 그 결과를 합하여 두 쿼터니언 사이의 내적을 연산할 수 있다:



우리는 또한 두 쿼터니언 사이의 각도의 차이를 계산하기 위해 쿼터니언의 내적을 사용할 수 있다:



그리고 단위-크기 쿼터니언을 위해, 우리는 식을 간단하게 할 수 있다:



Rotations
너가 기억한다면, 2D 복소 평면을 통해 한 점을 회전시키기 위해 사용될 수 있는 Rotor라고 불려지는 복소수의 특별한 형태를 정의했었다:



그러고나서 복소수와의 유사성으로 인해, 3D 공간에서의 한 점을 회전시키는데 사용될 수 있는 한 쿼터니언을 표현하는 것이 가능해져야 한다.



이 이론이 쿼터니언의 q와 벡터 p의 곱을 연산하여 유효한지 검증해보자. 처음에, 우리는 p는 Pure quaternion의 형태로 나타낼 수 있다:



그리고 q는 단위-크기 쿼터니언의 형태이다:



그러고나서



우리는 그 결과가 스칼라와 벡터 부분 둘 다를 가진 일반 쿼터니언이라는 것을 볼 수 있다.

처음에 bold p가  v_hat에 수직인 특별한 경우를 봐보자. 그 경우에 내적 항은 가 되고 그 결과는 Pure quaternion이 된다:



이 경우에, p를 v_hat에 대해서 회전시키는 것을 s = cos(theta)로 그리고 labmda = sin(theta)로 치환해보자.



한 예제로, 한 벡터 bold_p를 z축에 대해서 45도 회전시켜 보자. 우리의 쿼터니언 q는:



그리고 bold_p가 bold_k에 수직인 특별한 경우를 고수하는 vector bold_p를 취해보자:



이제 qp의 곱을 해보자:



이것은 bold_k 축에 대해 45도 회전한 순수 쿼터니언을 만들어 낸다. 우리는 또한 그 결과 벡터의 크기가 유지되는것을 확인할 수 있다:



그리고 이것이 우리가 기대했던 결과이다.

우리는 다음의 이미지로 이것을 시각화 할 수 있다.

이제 bold_p에 직교하지 않은 쿼터니언을 고려해보자. 만약 우리가 얻은 p로부터 45도 변위에 대한 우리의 쿼터니언의 벡터 부분을 명시하자면:



그리고 우리의 벡터 p를 q로 곱하여 우리는 다음을 얻는다:



v_hat과 bold_p를 치환하고 theta를 45도로 치환하는 것은 다음을 준다:



이것은 더 이상 puer quaternion이 아니다, 그리고 45도가 회전 되지 않았다. 그래서 벡터의 크기가 더 이상 2가 아니다 (대신에 그것은 root(3)이 되었다, 쿼터니언의 스칼라 부분을 포함하지 않고 vector 부분만 표준화하면).

그 결과는 이미지로 시각화 될 수 있다.

! 기술적으로, 3차원 공간에서 쿼터니언 p'를 표현하는 것은 부정확하다. 왜냐하면 그것은 4D 벡터이기 때문이다! 간단하게 하기 위해서, 나는 오직 쿼터니언의 벡터 요소만을 시각화할 것이다.

그러나 모든 것이 잃어진 것은 아니다. Hamilton은 만약 우리가 qp의 결과에 q의 역을 나중에 곱한다면 그 결과가 puer quaternion이고 벡터 component의 크기가 유지된다는 것을 인지했다. (출판하지 않았지만). 우리가 이것을 우리의 예제에 적용할 수 있는지 봐보자.

처음에  q^-1을 계싼하자:



theta가 45인 것에 대해,



그리고 이전의 qp 값에 q^-1을 합하는 것은 다음을 준다:



이것은 pure quaternion이고 그 결과의 크기는:



그리고 이것은 p와 같은데, 그래서 벡터의 크기가 유지된다.

아래의 이미지는 그 회전의 결과를 시각화한다.

그래서 우리는 그 결과가 pure quaternion이고 그 초기 벡터의 크기가 유지된다는 것을 볼 수 있지만, 그 벡터가 45도보다 바라는 것의 두 배인 90도 회전되었다는 것을 볼 수 있다.

그래서 정확하게 vector bold_p를 임의의 축 v_hat에 대해 각 theta만큼 회전시키기 위해서, 우리는 반각을 고려해야하고, 다음의 쿼터니언을 구성한다:



그리고 이것이 회전 쿼터니언의 일반 형식이다!

Quaternion Interpolation
컴퓨터 그래픽스에서 쿼터니언을 사용하는 가장 중요한 이유들 중 하나는 쿼터니언이 공간에서 회전을 나타내는데 매우 좋다는 것이다. 쿼터니언들은 3D 공간에서 점을 회전 시키는 것을 오염시키는 Gimbal lock같은 문제를 극복한다. Gimbal lock은 너가 너의 회전을 오일러 각으로 나타낼때 발생하는 문제이다.

쿼터니언을 사용하여, 우리는 3D 공간에서 rotational interpolation을 나타내는 몇 가지 방법을 정의할 수 있다. 내가 검증할 첫 번째 방법은 SLERP라고 불리는데, 그것은 두 방향 사이의 한 점을 부드럽게 보간하기 위해서 사용된다. 두 번째 방법은 SLERP의 확장인 SQAD인데, 이것은 한 경로를 정의하는 방향의 순서를 통해 보간하기 위해 사용된다.

SLERP
SLERP는 Spherical Linear Int!erp!olation을 말한다. SLERP는 두 방향에 대해 한 점을 부드럽게 보간하는 방법을 제공한다.

나는 첫 번째 방향을 q_1으로 나타내고, 두 번째 방향을 q_2로 나타낼 것이다. 그 점은 bold_p로 나타내어질 것이고, 그 보간된 점은 p'로 나타내어질 것이다. interpolation parameter t는 t= 0일 때, bold_p를 q_1로부터 interpolate할 것이다. t = 1일때 q_2에 대해 할 것이다.

표준 선형 보간 공식은:



이 방정식을 적용하는 일반적인 단계는 :

• bold_p1과 bold_p2 사이의 차이를 계산해라
• 그 차이의 유리수 부분을 가져와라
• 두 점 사이의 유리수 부분으로 원래 값을 조정해라

우리는 두 쿼터니언 방향 사이에서 interpolate하기위해 간단한 기본 원칙을 사용할 수 있다.

1. Quaternion difference

첫 번째 단계는 우리가 q_1과 q_2의 차이를 연산해야만 하는 것이다. 쿼터니언과 관련해서, 이것은 두 쿼터니언 사이의 각도의 차를 연산하는 것과 같다.

2. Quaternion Exponentation

다음 단계는 그 차이의 유리수 부분을 가져오는 것이다. 우리는 값이 [0..1]의 범위에 있는 것으로 지수승하여 쿼터니언의 소수 부분을 계산할 수 있다.

쿼터니언의 지수승의 일반적이 공식은 :

여기에서 쿼터니언의 지수함수는 :

(이것은 e^iΘ = cosΘ + isinΘ 이기 떄문에 식이 저렇게 바뀐다.)

그리고 쿼터니언의 로그는 :


t = 0에 대해서, 우리는



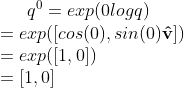
그리고 t=1에 대해서



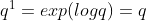
3. Fractional Difference of Quaternions
interpolated된 각 회전을 연산하기 위해서, 우리는 원래 방향 q_1을 q_!과 q_2 사이의 차이의 소수 부분으로 조정해야 한다.



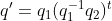
그리고 이것은 쿼터니언을 사용한 spherical linear interpolation의 일반 형태이다. 그러나, 이것은 실제로 흔히 사용되는 SLERP 공식의 형태가 아니다.

우리는 쿼터니언들에 대해 spherical interpolation을 수행하기 위해 유사한 공식을 적용할 수 있다. 벡터에 대한 spherical interpolation의 일반 형태는 다음과 같이 정의된다:



이것은 다음의 이미지로 시각화 된다.

이 공식은 쿼터니언에 수정되지 않은 채로 적용될 수 있다:



그리고 q_1과 q_2사이의 내적을 하여 각 theta를 구한다.



4. Consderations
구현하는 동안 구현과 관련하여 고려해야 할 두 가지 문제들이 있다.

첫 째로, 만약 쿼터니언 내적이 음수값을 만들어낸다면, 그러면 그 결과 interpolation은 우리가 필연적으로 원하는 것이 아닌 4D 구를 주변으로 "long-way"를 여행할 것이다. 이 문제를 해결하기 위해, 우리는 내적의 결과를 테스트할 수 있고, 그것이 음수라면, 그러면 우리는 그 방향 중 하나를 음수화할 수 있다. 쿼터니언의 스칼라와 벡터 부분을 음수화 하는 것은 그것이 나타내는 방향을 바꾸지 않는다. 그러나 이렇게 하여, 우리는 그 방향이 최단 거리에 적용될 것이라고 보장한다.

q_1과 q_2사이의 각의 차가 매우 작을 때 다른 문제가 발생한다. sin\theta가 0이 되는 것이다. 만약 이것이 발생하면, 우리는 sin\theta로 나눌 때 정의되지 않은 결과를 얻을 것이다. 이 경우에 우리는 q_1과 q_2사이의 linear interpolation하는 것에서 물러날 수 있따.

SQUAD
SLERP가 두 쿼터니언 사이의 보간을 연산하기 위해 사용될 수 있는 것처럼, SQUAD(Spherical and Quadrangle)은 회전의 경로에 대해 부드럽게 보간하기 위해 사용될 수 있다.

만약 우리가 쿼터니언의 연속을 가지고 있따면:

   q_1, q_2, ... q_n

그리고 우리가 또한 "helper" 쿼터니언 s_i를 정의한다면, 우리는 이것을 중간 control point로 고려할 수 있다:



그리고 이것에 의해 정의되는 부분-cuve를 따라가는 방향은:

  q_(i-1), q_i, q_(i+1), q_(i+2)

시간 t에서 주어지면



Conclusion

이해하기 극히 어려움에도 불구하고, 쿼터니언들은 회전을 나타내기 위해 행렬 또는 오일러 각을 사용하는 것보다 명백한 이점들을 제공한다.

• SLERP와 SQUAD를 사용한 Quaternion interpolation은 공간에서 방향 사이를 부드럽게 보간하는데 방법을 제공한다.
• 쿼터니언을 사용한 회전의 연결은 행렬 형태로 표현되는 회전을 결합하는 것보다 더 빠르다.
• 단위크기의 쿼터니언에 대해, 회전의 역은 쿼터니언의 벡터 부분을 뺴서 취해진다. 한 회전 행렬의 역행렬은 만약 그 행렬이 직교화되지 않았다면 상당히 느리다. (만약 직교행렬이라면, 그 역행렬의 전치행렬이다.)
• 쿼터니언을 행렬로 바꾸는 것은 오일러 각에대한 것보다 조금 더 빠르다.
• 쿼터니언들은 회전을 표현하기 위해 4개의 숫자를 요구한다. (만약 그것들이 정규화 된다면 3개. 실수부는 런타임에 계산되어질 수 있다) 그리고 거기에서 한 행렬은 적어도 9개의 값을 요구한다.

쿼터니언을 사용하는것을 옹호하는 모든 이점에 대해, 다른 불이익들이 있다.

• 쿼터니언들은 부동소수점 반올림 에러 때문에 유효하지 않을 수 있다. 그러나 이 "error creep"은 쿼터니언을 re-normalizing하여 해결될 수 있다.
• 그리고 아마도 쿼터니언을 사용하는데에 대한 가장 큰 저지하는 요인은 그것들이 이해하기 어렵다는 것이다. 이 문제가 이 자료를 읽고나서 해결되기를 희망한다.

--------------------------------------------------------------------------------
여기까지 번역하면서, 쿼터니언의 연산과 회전에 대해서 어느정도 이론적으로 이해했으나, 이것을 가지고 아직 쿼터니언 카메라를 구현할 수 없었다.

그래서 실제 구현 관련되어 여러 자료들을 하나씩 읽어봐야 겠다.

https://developerblog.myo.com/quaternions/
https://www.gamasutra.com/view/feature/131686/rotating_objects_using_quaternions.php
https://gamedev.stackexchange.com/questions/30644/how-to-keep-my-quaternion-using-fps-camera-from-tilting-and-messing-up/30669#30669
http://www.euclideanspace.com/maths/geometry/rotations/conversions/angleToQuaternion/index.htm
https://gitlab.com/muffinman007/OpenGL_360_Camera_Quarternion/tree/master
https://learnopengl.com/Getting-started/Camera