Chapter 9 The Mathematics Of Rotations
- 2차원에서 오브젝트의 회전
2차원 오브젝트는 다음으로 표현된다
Position (x, y)
Orientation Angle
Position <-> Velocity <-> Acceleration
Orientation <-> Angular Velocity <-> Angular Acceleration
Angular Velocity 는 방향(Orientation)의 변화율 == 회전(Rotation)이라고 이 책에서 표현
- 각도(Angle)의 수학 (2차원)
* 라디안 표기법 (-𝝅, 𝝅] : 쓰기 어려움
* 벡터 표기법
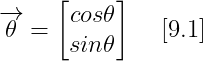
if 𝜭 == 0, 방향은 양의 X축을 가리키고 있다. (일반적인 극좌표계)
𝜭가 증가함에 따라 반시계 방향으로 돌아간다.
이 벡터 표기법은 Special case code가 덜 필요하고, Bounds-checking을 덜하게 된다.
* 자유도(A degree of freedom) : 다른 것과 독립적으로 바꿀 수 있는 어떤 Quantity
그냥 방향만을 나타낼 때 단일의 scalar 값으로도 나타낼 수 있는데,
2D로 갈 때, 방향을 나타내는데, 자유도가 한 개 추가 되었다.
그래서 벡터 표기법에서 크기가 1이여야 하는 제약이 추가 되었다.
{
자유도가 하나 추가될 때 마다, 그에 상응하는 제약이 추가되는 것 같다.
}
- Angular Speed (2차원)
한 오브젝트의 angular speed = rotation
단일 scalar value로서, 모든 Angular speed는 unique하다.
Bounds-checking, special case code 필요 없다.
- Origin and Center of Mass (2차원)
The "Origin" of an object : 큰 오브젝가 어떤 위치에 있을 때, (보통) 그 오브젝트 안에 미리 정의된 한 점. (그러니까, World Coordinate에 한 오브젝트의 위치를 점으로 표시하는데, 나중의 Center of Mass를 위해서, 그 때 오브젝트 좌표계(Local Coordinate)에서의 한 점의 위치를 정하는데, 그게 Origin of an object가 된다.)
(1) 평행이동 Case
예를들어 [a ,b]가 origin of an object이고, 그 오브젝트가 [c, d]만큼 평행이동(translation)되었다면 [a + c, b +d]가 월드 좌표계의 origin of the object가 된다.
(2) 평행이동 + 회전 Case
q_b가 origin of an object라면, 평행이동이 p만큼 되고 theta만큼 회전되었다면
을 통해 World Coordinates에서의 origin of the object가 구해진다.
즉, 어떤 조합의 회전과 평행이동이 오든, 단일 회전 후의 단일 평행이동과 같다.
(3) Rigid Body에 대해
한 오브젝트의 모든 컴포넌트 (구성된 모든 파티클들)들이 그것의 origin(원점)을 기준으로 고정되어 있다는 사실이 물리엔진에서 Rigid Bodies에 대해 고려하는 이유이다.
이때 Rigid Body의 Center of Mass(CM)을 원점으로 설정하면 수학이 훨씬 더욱 간단해진다 (이전 게시글의 Chris Hecker Article 1에서 CM에 대한 식을 유도했다)
CM을 통해 하나의 파티클처럼 linear motion과 angular motion으로 Rigid Body의 움직임을 분해할 수 있다.
- 3차원에서의 회전
2차원 회전은 Single Value of Angle ->Vector 표기로 되었다.
3차원 회전
(1) Euler Angles
회전에 대한 세 개의 자유도(Degree of Freedom)
Yaw Pitch Roll
Y X Z
각 축에 대한 회전의 양이 Euler Angles이다.
그러나, 각 축에 대한 회전을 적용시키는 순서에 따라 결과가 다르다. 회전의 교환법칙이 적용되지 않는다.
게다가, 한 축이 다른 축과 정렬되어 회전을 올바로 표기할 수 없는 Gimbal lock 문제가 생긴다.
2차원 오브젝트는 다음으로 표현된다
Position (x, y)
Orientation Angle
Position <-> Velocity <-> Acceleration
Orientation <-> Angular Velocity <-> Angular Acceleration
Angular Velocity 는 방향(Orientation)의 변화율 == 회전(Rotation)이라고 이 책에서 표현
- 각도(Angle)의 수학 (2차원)
* 라디안 표기법 (-𝝅, 𝝅] : 쓰기 어려움
* 벡터 표기법
if 𝜭 == 0, 방향은 양의 X축을 가리키고 있다. (일반적인 극좌표계)
𝜭가 증가함에 따라 반시계 방향으로 돌아간다.
이 벡터 표기법은 Special case code가 덜 필요하고, Bounds-checking을 덜하게 된다.
* 자유도(A degree of freedom) : 다른 것과 독립적으로 바꿀 수 있는 어떤 Quantity
그냥 방향만을 나타낼 때 단일의 scalar 값으로도 나타낼 수 있는데,
2D로 갈 때, 방향을 나타내는데, 자유도가 한 개 추가 되었다.
그래서 벡터 표기법에서 크기가 1이여야 하는 제약이 추가 되었다.
{
자유도가 하나 추가될 때 마다, 그에 상응하는 제약이 추가되는 것 같다.
}
- Angular Speed (2차원)
한 오브젝트의 angular speed = rotation
단일 scalar value로서, 모든 Angular speed는 unique하다.
Bounds-checking, special case code 필요 없다.
- Origin and Center of Mass (2차원)
The "Origin" of an object : 큰 오브젝가 어떤 위치에 있을 때, (보통) 그 오브젝트 안에 미리 정의된 한 점. (그러니까, World Coordinate에 한 오브젝트의 위치를 점으로 표시하는데, 나중의 Center of Mass를 위해서, 그 때 오브젝트 좌표계(Local Coordinate)에서의 한 점의 위치를 정하는데, 그게 Origin of an object가 된다.)
(1) 평행이동 Case
예를들어 [a ,b]가 origin of an object이고, 그 오브젝트가 [c, d]만큼 평행이동(translation)되었다면 [a + c, b +d]가 월드 좌표계의 origin of the object가 된다.
(2) 평행이동 + 회전 Case
q_b가 origin of an object라면, 평행이동이 p만큼 되고 theta만큼 회전되었다면
을 통해 World Coordinates에서의 origin of the object가 구해진다.
즉, 어떤 조합의 회전과 평행이동이 오든, 단일 회전 후의 단일 평행이동과 같다.
(3) Rigid Body에 대해
한 오브젝트의 모든 컴포넌트 (구성된 모든 파티클들)들이 그것의 origin(원점)을 기준으로 고정되어 있다는 사실이 물리엔진에서 Rigid Bodies에 대해 고려하는 이유이다.
이때 Rigid Body의 Center of Mass(CM)을 원점으로 설정하면 수학이 훨씬 더욱 간단해진다 (이전 게시글의 Chris Hecker Article 1에서 CM에 대한 식을 유도했다)
CM을 통해 하나의 파티클처럼 linear motion과 angular motion으로 Rigid Body의 움직임을 분해할 수 있다.
- 3차원에서의 회전
2차원 회전은 Single Value of Angle ->Vector 표기로 되었다.
3차원 회전
(1) Euler Angles
회전에 대한 세 개의 자유도(Degree of Freedom)
Yaw Pitch Roll
Y X Z
각 축에 대한 회전의 양이 Euler Angles이다.
그러나, 각 축에 대한 회전을 적용시키는 순서에 따라 결과가 다르다. 회전의 교환법칙이 적용되지 않는다.
게다가, 한 축이 다른 축과 정렬되어 회전을 올바로 표기할 수 없는 Gimbal lock 문제가 생긴다.
Gimbal Lock Explained with Video
https://youtu.be/zc8b2Jo7mno
https://youtu.be/rrUCBOlJdt4
즉, 순서가 Y->X->Z 순으로 될 때, Y는 X와 Z축에 영향을 미치고, X축을 Z축에 영향을 미치게 된다. 이 때 X축을 90도 회전시키면, Z축은 Y축과 정렬되게 되낟. 그래서 Y축과 Z축이 같은 방향을 가리키게 되어있어, 올바른 세 방향을 나타낼 수 없다. 이걸 해결하려면 X를 다시 돌려야 한다. 정렬된 상태에서 Y축을 돌리게 되면 회전이 직선이 아니라, 이상한 예상치 않은 방향으로(곡선)으로 회전하게 된다.
(2) Axis-Angle
Axis-Angle : 고정된 축에 대한 한 각도
축에 대한 한 벡터와 각도는 4개의 자유도를 주는데, 회전은 오직 세 개의 자유도이므로,
그 추가 자유도는 벡터가 표준화 되는 것을 요구하여 제거된다.
게다가 Scale Axis Representation도 있지만,여러 문제가 있다.
(3) Rotation Matrices
2차원에서 회전행렬은
이였지만,
3차원에서는 Rodriues Rotation Formula를 사용해서 한다.
Wikipedia : Rodrigues' Rotation Formula
https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula
An easy derivation of 3D rotation matrices (로드리게스 회전 공식을 사용하여 쉽게 설명)
https://diego.assencio.com/?index=b155574a293a5cbfdd0fbe82a9b8bf28
즉,
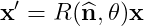
회전축 n에 대해 x벡터를 𝜭만큼 회전시키는 것이다.
그러나, 이것을 주로 사용하게 된다면, 9개의 자유도로 인해 부동 소수점 연산의 부정확성으로 인해, 그것을 정확하게 해주는 adjustment process가 자주 필요하게 된다. 이것은 많은 연산량을 소모시킨다.
(4) Quaternion
https://chanhaeng.blogspot.com/2018/09/quaternions-and-rotations.html
이 식에 대한 것은 이 링크를 통해 공부할 것.
쿼터니언의 자유도는 4, 회전의 자유도는 3,
그래서 쿼터니언의 크기가 1이여야 한다는 제약이 있다.
- Angular Velocity
Rigid Body가 얼마나 빠르게 그리고 무슨 방향으로 회전하는지 알아야 한다.
2차원 Angular Velocity에 single value를사용. Bounds Checking 필요 없음
3차원 Scaled Axis Representation을 사용.
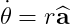
r은 회전하고 있는비율 : Radians per second
a는 오브젝트의 회전축.
𝞈는 한 새로운 방향으로 어떤 rate의 회전을 말한다.
linear velcoity로 position을 업데이트하는 것은
angular velocity로 orientation을 업데이트하는 것은
위의 식에 대한 증명은 맨 밑의 David Baraff 논문에 설명되어 있다. 쿼터니언의 변화량 그러니까 방향의 변화량, 쿼터니언 미분을 통해서 이 식을 유도해낸다.
- The Velocity of A Point
한 오브젝트 위에 있는 한 점의 속도는 그것의 linear and angular velocity에 의존한다.
dot(q) = 점의 속도
q = 점의 월드좌표계 위치
p = 오브젝트의 원점 위치
theta = 오브젝트의 Angular Velocity
- Angular Acceleration
- Implementing the Mathematics
나머지 것들은 그렇게 어렵지 않고 그나마 중요한 행렬의 기저 변환만 설명.
An easy derivation of 3D rotation matrices (로드리게스 회전 공식을 사용하여 쉽게 설명)
https://diego.assencio.com/?index=b155574a293a5cbfdd0fbe82a9b8bf28
즉,
회전축 n에 대해 x벡터를 𝜭만큼 회전시키는 것이다.
그러나, 이것을 주로 사용하게 된다면, 9개의 자유도로 인해 부동 소수점 연산의 부정확성으로 인해, 그것을 정확하게 해주는 adjustment process가 자주 필요하게 된다. 이것은 많은 연산량을 소모시킨다.
(4) Quaternion
https://chanhaeng.blogspot.com/2018/09/quaternions-and-rotations.html
이 식에 대한 것은 이 링크를 통해 공부할 것.
쿼터니언의 자유도는 4, 회전의 자유도는 3,
그래서 쿼터니언의 크기가 1이여야 한다는 제약이 있다.
- Angular Velocity
Rigid Body가 얼마나 빠르게 그리고 무슨 방향으로 회전하는지 알아야 한다.
2차원 Angular Velocity에 single value를사용. Bounds Checking 필요 없음
3차원 Scaled Axis Representation을 사용.
r은 회전하고 있는비율 : Radians per second
a는 오브젝트의 회전축.
𝞈는 한 새로운 방향으로 어떤 rate의 회전을 말한다.
linear velcoity로 position을 업데이트하는 것은
angular velocity로 orientation을 업데이트하는 것은
위의 식에 대한 증명은 맨 밑의 David Baraff 논문에 설명되어 있다. 쿼터니언의 변화량 그러니까 방향의 변화량, 쿼터니언 미분을 통해서 이 식을 유도해낸다.
- The Velocity of A Point
한 오브젝트 위에 있는 한 점의 속도는 그것의 linear and angular velocity에 의존한다.
dot(q) = 점의 속도
q = 점의 월드좌표계 위치
p = 오브젝트의 원점 위치
theta = 오브젝트의 Angular Velocity
- Angular Acceleration
- Implementing the Mathematics
나머지 것들은 그렇게 어렵지 않고 그나마 중요한 행렬의 기저 변환만 설명.
행렬의 기저 변환
https://www.youtube.com/watch?v=P2LTAUO1TdA
M_b = M_a M_t M_a^-1
이렇게 되어있는데, 링크의 유튜브 영샹에 따르면
M_b = M_a^-1 M_t M_a 요렇게 된다.
근데 기저행렬이라면 세 행 또는 열이 모두 직교하므로, inverse는 곧 transpose이므로
상관 없다.
그러니까, 어떤 기저로 바꿀지 잘 보아서 행렬 식을 잘 쓰면 될 것이다.
M_b = M_a M_t M_a^-1
이렇게 되어있는데, 링크의 유튜브 영샹에 따르면
M_b = M_a^-1 M_t M_a 요렇게 된다.
근데 기저행렬이라면 세 행 또는 열이 모두 직교하므로, inverse는 곧 transpose이므로
상관 없다.
그러니까, 어떤 기저로 바꿀지 잘 보아서 행렬 식을 잘 쓰면 될 것이다.
Chris Hecker Article 2
이 자료는 Angular Effects에 대한 설명이다. Angular Effects 전반, Torque까지 다룬다. 2차원을 기반으로 하는 설명이라는 것을 염두에 두어야 한다.
이 공식은 forces가 어디에서 오는지에 대한 개념을 포함하고 있지 않다.
그러한 힘들이 body를 어떻게 회전 시키는지에 대해 알아내는데 있어서 중요한 것이 있다.
Figure 1 The Definition of 𝛀 참조
또 다른 Kinematic Quantity인 Orientation, 𝛀, Capital Omega가 있다.
이것은 Rigid Body에 고정된 좌표계(Local Coordinates)와 고정된 World Coordinates 사이의 Angular Difference in Radians 이다.
𝛀는 반 시계 방향으로 양수이다.
𝛀가 변화한다 -> 새로운 Kinematic Quantity 도입
즉, Angular Velocity, 𝛚, lowercase omega.
dot(𝛀)를 잘 표기하지는 않지만
dot(𝛚)는 Angular Acceleration으로서 표현하기도 한다.
Angular Acceleration은 𝛂이고, lowercase alpha이다.
따라서,
body가 회전하고 있으면, body에 있는 임의의 점의 속도를 단순 linear velocity로 구할 수 없다.
그래서 이 상황을 해결하기 위해 다음의 상황을 만들어 낸다.
Assumption Case : body가 translation(평행이동)하지 않고 rotating하고 있다. 이 body는 원점 O에 고정되어 있다.
이 회전하는 body 위에 있는 한 점 B의 velocity를 계산하는 식은
𝛚, omega(angular velocity)옆에 있는 것의 subscript에 있는것은 perpendicular operator로서 그 벡터에 수직인 것을 구하는 것이다. 즉, r^{OB} 벡터를 반시계 방향으로 90도 회전시킨다. 2D에서는 perp op(perpendicular operator)는 다음과 같이 쉽게 된다.
위의 Eq.7에 대한 증명은 두 가지가 필요하다.
1. 결과 Velocity Vector의 크기가 옳다
2. 그 벡터가 옳은 방향을 가리키고 있다.
먼저 첫 번째 부터 증명할 것이다.
* Prove 1 : Eq.7의 결과 Velocity Vector의 크기는 옳다
Figure C = 𝛀r 참조
C = 𝛀r에서, 𝛀는 radians이고, r은 원점에서 점 B까지 가는 벡터의 길이이다. C는 호의 길이가 되는데, 우리가 잘 아는 호의 길이 공식 l = r𝜽도 있지만, radians의 의미를 알면 더 쉽다.
라디안은 원의 반지름에 의해 스케일링 되는 호의 길이의 척도가 된다. 그래서 원주가 2𝞹r 이 되는 것이다.
한 점의 Speed는 시간에 대한 Position의 변화이다. (점 B에서 C만큼(호의길이만큼) 움직이기 때문에, Position의 변화량은 C가 되는 것이다) ->
그리고 그것은 Velocity Vector의 크기라고 할 수 있다. (벡터는 방향과 크기를 가지므로, 그 변화량을 표현하는 것이 크기이다) ->
움직임은 시간에 대해 미분하여 B의 속도를 찾을 수 있다. ->
C = 𝛀r이 그 움직임에 대한 공식이다. (즉, C = 𝛀r을 미분해보자)
r은 상수여서(길이) 미분에서 떨어져 나오고, 𝛀의 시간에 대한 미분은 (Eq.6)에 의해 𝛚이다. 따라서 점 B의 velocity vector의 크기는 𝛚r 이된다.
따라서
의 크기는 옳다. perp operator는 크기를 변화시키지 않기 때문이다.
* Prove 2 : Eq.7의 결과 Velocity Vector는 옳은 방향을 가리키고 있다.
이 증명을 제대로 하려면, 고정 길이 벡터의 내적 미분을 해야한다. 여기서는 직관적인 설명으로 증명한다.
Velocity vector의 방향은 radius vector에 수직해야 한다.
왜냐하면,
또 다른 고정점에 대해 회전하는 한 점은 어떤 매우 짧은 순간에서 점들 사이의 벡터에 수직하게만 움직일 수 있기 때문이다. (이것은 Unit Circle을 원점에 그려서, 그 원을 엄청나게 확대해서, 엄청나게 확대된 한 점이 시계 반대 방향으로 한 점을 또 이동하려면 원점에서 확대된 점의 radius vector에 수직하게 움직여야 최적이라는 것이 직관적이게 될 것이다.)
마지막으로 결과 velocity vector의 부호가 맞는지 확인해야 한다.
perp op는 사실 두 방향을 골라야 한다. 시계 반대인지 시계 방향인지.
𝛀가 시계 반대 방향이고,
𝛚가 시계 반대 방향일 때 양수이다.
그리고 perp op는 시계 반대방향으로 돌리기 때문에,
최종적으로 결과 velocity vector는 옳은 방향을 가리키고 있다.
따라서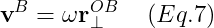
가 증명된다.
이제, Eq.7의 제한된 사용에서(translation없음) 벗어나서 확장을 해야한다 ->
Bodies를 동시에 회전시키고 평행이동 시키기 ->
이것은 Rigid Body의 단일 점의 Simple Translation + 그 단일 점을 중심으로 몸의 나머지의 Simple Rotation을 해야 한다 ->
이것은 Chasles' Theorem이라고 한다 ->
즉, Motion은 Linear Component와 Angular Component로 분해된다.
따라서
즉, body의 origin의 known linear velocity를 취하고, 거기에 그 body의 회전으로 생성된 velocity를 더해서 움직이는 body의 어떤 점의 속도를 계산할 수 있다.
𝛚가 시계 반대 방향일 때 양수이다.
그리고 perp op는 시계 반대방향으로 돌리기 때문에,
최종적으로 결과 velocity vector는 옳은 방향을 가리키고 있다.
따라서
이제, Eq.7의 제한된 사용에서(translation없음) 벗어나서 확장을 해야한다 ->
Bodies를 동시에 회전시키고 평행이동 시키기 ->
이것은 Rigid Body의 단일 점의 Simple Translation + 그 단일 점을 중심으로 몸의 나머지의 Simple Rotation을 해야 한다 ->
이것은 Chasles' Theorem이라고 한다 ->
즉, Motion은 Linear Component와 Angular Component로 분해된다.
따라서
즉, body의 origin의 known linear velocity를 취하고, 거기에 그 body의 회전으로 생성된 velocity를 더해서 움직이는 body의 어떤 점의 속도를 계산할 수 있다.
이제 translation과 rotation으로 인한 한 점의 속도를 알게 되었으니
Angular Momentum을 알아보자.
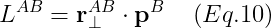
L^{AB}는 다른 점 A에 대한 한 점 B의 Angular Momentum이다. (A가 회전의 중심점이라고 생각하면 된다)
Angular Momentum은 Linear Momentum과 다르게 특정한 점으로 부터 (예를들어, A로부터) 측정된다.
우변에서 p^B는 점 B의 linear momentum을 나타낸다.
Angular Momentum을 구하는 식을 보게된다면, perp dot product를 하게 된다 (perp dot product는 3D cross product와 유사한 것이다).
이것은 자료에 있는 그림을 참고해본다면,
Angular Momentum은 A와 관련한 방향의 회전에서 B의 linear momentum이 얼마나 많이 있는지에 대한 측정이다.
나의 직관으로 설명해보자면, perp op가 실행되는 벡터를 생각하면, A의 중심점에서 B까지의 벡터가 길이를 가지고, perp op로 회전의 방향을 가지게 되는데, 이 때 그 벡터에 B에서의 linear momentum과의 내적을 통해 그 길이를 가진 회전이 얼마만큼 영향을 받는지를 보여주는 것 같다. 그래서 Angular Momentum이 이런 식으로 식이 만들어진 것 같다.
{
이전 자료에서 그랬듯이 운동량에 대한 식의 도출, 그러니까
p = mv
L^AB = dot(r^AB_perp, p^B) 같은 식들에 대한 유도는 설명하지 않고 그냥
식이 나타난다. 아마 이것을 유도하려면 물리와 수학 쪽에 깊게 들어가야 하나보다.
그래서, 이런 식들은 그냥 나의 직관으로 이렇게 되겠구나 이해하고 넘어가야 할 듯 하다.
}
이제 Angular Momentum에 대해 알았으니, 이걸로 Force에 대한 식을 구했던 것처럼 Torque를 알아볼 시간이다!
즉, Force를 정의하기 위해 Linear Momentum을 미분했듯이,
Torque를 정의하기 위해 Angular Momentum를 미분한다.
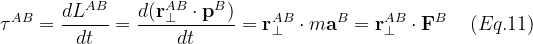
즉, torque는 특정 점의 force가 perp dot product와 연관된다.
점 B에 적용된 force가 점 A를 기준으로 얼마나 많이 회전하는지를 측정하는 것이다.
따라서 force에 대한 회전이 torque이다.
Eq.11은 적용된 force와 force의 적용점으로 부터 torque를 계산하게 해준다.
Torque 식을 통해 우리는 Dynamics 방정식을 알았지만
Torque <-> Orientation, Angular Velocity, Angular Acceleration
의 관계를 모른다. 더 방정식을 유도해야 한다.
먼저 CM을 위해 F^T에 대해 했던 것처럼 유사한 과정을 하게 될 것이다.
점 A에 대한 Total Angular Momentum
Eq.12는 점 A로부터 측정되는 모든 점의 모든 angular momentums의 합이다. widehat{A}_i 표기는 그것의 오른쪽에 있는 연산의 summation이라고 생각하면 된다.
이제 위의 식을 한 점의 속도 방정식인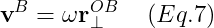 으로 간단하게 만들 것이다.
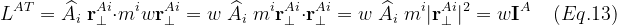
마지막에서 두 번째 식에서는 r^{Ai}_\perp의 길이의 제곱이다.
마지막 식에서 I^A는, A점에서의 Rigid Body의 The moment of inertia이다.
m^i와 r^{Ai}_\perp는 Rigid Body에 대해 이제 상수가 된다. 고정되기 때문이다.
그래서 우리는 The moment of Inertia(관성모멘트)를 구해놓고 계속 쓸 수 있는 것이다.
I^A는 Body에서 A에서각 다른점 까지의 제곱 거리의 합인데, 그 제곱 거리가 각 점의 질량으로 스케일링 되었다.
쉽게 말해, 점 A에 대해 그 몸체를 얼마나 세게 회전 시킬지에 대한 단위이다.
그래서 글쓴이는 연필의 예를 들려준다. 연필의 중심지에서 힘을주어서 회전시키는 것은 쉽지만. 연필의 끝에서 회전시키는 것은 어렵다. 끝 부분에서 끝 부분까지의 거리의 제곱으로 인한 관성모멘트가 크기 때문이다.
Angular Momentum을 알아보자.
L^{AB}는 다른 점 A에 대한 한 점 B의 Angular Momentum이다. (A가 회전의 중심점이라고 생각하면 된다)
Angular Momentum은 Linear Momentum과 다르게 특정한 점으로 부터 (예를들어, A로부터) 측정된다.
우변에서 p^B는 점 B의 linear momentum을 나타낸다.
Angular Momentum을 구하는 식을 보게된다면, perp dot product를 하게 된다 (perp dot product는 3D cross product와 유사한 것이다).
이것은 자료에 있는 그림을 참고해본다면,
Angular Momentum은 A와 관련한 방향의 회전에서 B의 linear momentum이 얼마나 많이 있는지에 대한 측정이다.
나의 직관으로 설명해보자면, perp op가 실행되는 벡터를 생각하면, A의 중심점에서 B까지의 벡터가 길이를 가지고, perp op로 회전의 방향을 가지게 되는데, 이 때 그 벡터에 B에서의 linear momentum과의 내적을 통해 그 길이를 가진 회전이 얼마만큼 영향을 받는지를 보여주는 것 같다. 그래서 Angular Momentum이 이런 식으로 식이 만들어진 것 같다.
{
이전 자료에서 그랬듯이 운동량에 대한 식의 도출, 그러니까
p = mv
L^AB = dot(r^AB_perp, p^B) 같은 식들에 대한 유도는 설명하지 않고 그냥
식이 나타난다. 아마 이것을 유도하려면 물리와 수학 쪽에 깊게 들어가야 하나보다.
그래서, 이런 식들은 그냥 나의 직관으로 이렇게 되겠구나 이해하고 넘어가야 할 듯 하다.
}
이제 Angular Momentum에 대해 알았으니, 이걸로 Force에 대한 식을 구했던 것처럼 Torque를 알아볼 시간이다!
즉, Force를 정의하기 위해 Linear Momentum을 미분했듯이,
Torque를 정의하기 위해 Angular Momentum를 미분한다.
즉, torque는 특정 점의 force가 perp dot product와 연관된다.
점 B에 적용된 force가 점 A를 기준으로 얼마나 많이 회전하는지를 측정하는 것이다.
따라서 force에 대한 회전이 torque이다.
Eq.11은 적용된 force와 force의 적용점으로 부터 torque를 계산하게 해준다.
Torque 식을 통해 우리는 Dynamics 방정식을 알았지만
Torque <-> Orientation, Angular Velocity, Angular Acceleration
의 관계를 모른다. 더 방정식을 유도해야 한다.
먼저 CM을 위해 F^T에 대해 했던 것처럼 유사한 과정을 하게 될 것이다.
점 A에 대한 Total Angular Momentum
Eq.12는 점 A로부터 측정되는 모든 점의 모든 angular momentums의 합이다. widehat{A}_i 표기는 그것의 오른쪽에 있는 연산의 summation이라고 생각하면 된다.
이제 위의 식을 한 점의 속도 방정식인
마지막에서 두 번째 식에서는 r^{Ai}_\perp의 길이의 제곱이다.
마지막 식에서 I^A는, A점에서의 Rigid Body의 The moment of inertia이다.
m^i와 r^{Ai}_\perp는 Rigid Body에 대해 이제 상수가 된다. 고정되기 때문이다.
그래서 우리는 The moment of Inertia(관성모멘트)를 구해놓고 계속 쓸 수 있는 것이다.
I^A는 Body에서 A에서각 다른점 까지의 제곱 거리의 합인데, 그 제곱 거리가 각 점의 질량으로 스케일링 되었다.
쉽게 말해, 점 A에 대해 그 몸체를 얼마나 세게 회전 시킬지에 대한 단위이다.
그래서 글쓴이는 연필의 예를 들려준다. 연필의 중심지에서 힘을주어서 회전시키는 것은 쉽지만. 연필의 끝에서 회전시키는 것은 어렵다. 끝 부분에서 끝 부분까지의 거리의 제곱으로 인한 관성모멘트가 크기 때문이다.
이제 Dynamics와 Kinematics의 관계에 우리는 들어갈 수 있게 되었다.
이제야 우리는 body에 대한 torque를 알면, 그것의 angular acceleration과 velocity, orientation을 알 수 있다.
즉,
그리고 적분을 통해 velocity, orientation를 알게 되는 것이다.
이제 우리는 2D에서 Full Rigid Body Physics의 모션을 재현하기 위해 위대한 것들을 다 얻었다. 상당히 많은 공식들이 지나갔지만, 다음의 알고리즘의 정리로 우리가 어느정도 고지에 도달했다는 것을 알게 될 것이다.
- Object의 CM 계산. Moment of Inertia 계산.
- Body의 position, orientation과 linear velocity와 angular velocity를 설정
- Body에 대한 모든 forces와 그것의 적용 지점을 알아낸다.
- 모든 forces를 합하고, CM의 linear acceleration을 찾기 위해 Total Mass로 나눈다 (Eq.5)
- 각 force에대해, CM -> Force 적용점으로 가는것의 perp dot product를 하고, 그 값을 CM에서의 total torque에 더해라 (Eq. 11)
- Angular Acceleration을 알기위해 Total torque를 CM에서의 관성모멘트로 나누어라.
- Numerically하게, linear acceleration과 angular acceleration을 적분해라. 그러면 position, linear velocity와 orientation, angular velocity를 업데이트 하게 된다 (여러가지 이슈 있음)
- 그 object를 새로운 position에서 그리고, step 3로 가라.
아직 안가르쳐 준 것
- CM에 대한 관성모멘트 계산 : 샘플 프로그램에 있음. 여러 물리책에 일반 오브젝트에 대한 관성모멘트가 있음. (CM에 대한 관성모멘트는 오브젝트의 표면에 대해 적분을 수행하여 이루어진다).
- 한 오브젝트에 대한 forces를 어떻게 알아내는가 (7번에서의 여러 이슈)
Part 3 Rigid Body Physics
Chapter 10 Laws Of Motion For Rigid Bodies
(위와 어느정도 중복된 자료도 있고, 여기는 구현도 많이 들어가 책을 보면서 하는 것을 추천)
- RigidBody Class
Transfor Matrix - Orientation + Position
- Newton 2 for Rotation
속도의 변화량
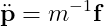
Angualar Velocity의 변화량
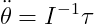
Angular acceleration은 force의 크기와 그 force가 적용되는 점이 얼마나 멀리 있는지에 의존한다.
p_f는 object의 origin(Center of Mass)를 기준으로 force가 적용되는 지점이고
f는 적용되는 force이다.
- RigidBody Class
Transfor Matrix - Orientation + Position
- Newton 2 for Rotation
속도의 변화량
Angualar Velocity의 변화량
Angular acceleration은 force의 크기와 그 force가 적용되는 점이 얼마나 멀리 있는지에 의존한다.
p_f는 object의 origin(Center of Mass)를 기준으로 force가 적용되는 지점이고
f는 적용되는 force이다.
즉, 한 오브젝트에 적용되는 모든 force는 대응 되는 torque를 방생시킨다.
10.1을 보면 f와 p_f가 같은 방향이면 torque는 zero가 된다.
즉, force의 연장선이 CM을 지나면 어떤 torque도 없다.
- The Moment of Inertia (관성모멘트) : Rotational Equivalent of Mass. 오브젝트의 회전 속도를 바꾸기 얼마나 어려운지에 대한 척도이다.
Inertia Tensor(Tensor는 어떤 차원의 배열인데, Rigid Body Physics에서는 항상 2x2이므로, Matrix 라고 봐도 무방하다) : 여러 축에 대한 관성모멘트를 표현한다.
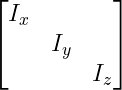
I_x,y,z : CM을 통해 그것의 각 축에 대해 그 오브젝트의 관성모멘트
나머지 항들은 products of inertia라고 불려진다.
{
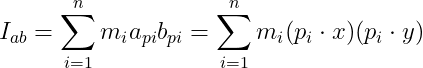
https://youtu.be/a9n2Ztp1Oic
https://www.youtube.com/watch?v=mFVz7iCc45I
https://www.youtube.com/watch?v=M_S4neYZ7CM
Rigid Body의 Inertia Tensor에 대한 유튜브 강의 들이 있다.
Inertia Tensor가 뭐하는 개념인지는 대충 아니까
그것의 유도를 나중에 시간날 때 들으면 좋을 것 같다.
}
그래서 Rigid Body에서 Torque를 구하는 식은 이 tensor를 이용하여
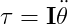
이렇게 되고, 우리가 알고싶은 Angular Acceleration은
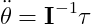[10.3]
그런데 위에 식에서, torque와 angular acceleration은 world coordinates에 있는데,
보통 Inertia tensor는 object의 local coordinates를 기준으로 두고 있다. 따라서, 우리는
inertia tensor in world coordinates를 구할 필요가 있다. 이 때 chapter 9에서 나온 기저변환을 사용한다.
좀 더 직관적으로 보여주자면
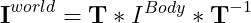
이런식으로 구성되고, T^-1은 transpose를 통해 연산량을 줄인다.
I^world라는 저렇게 계산된 inertia tensor world가 있다면, world 좌표계의 벡터 그러니까
우리의 목적인 torque in world coordinates와 I^world가 곱해진다고 해보자.
그러면 T^-1을 통해 우선적으로 torque은 local coordinates로 들어가게 되고,
torque in local coordinates는 I^Body와 같은 space에서 계산되어진다, 그렇게 계산되고난 후 다시 T를 통해 world 좌표계로 돌려지는 것이다.
이러한 과정이 I^world에 담겨있으므로, 우리는 기저변환하여 I^world에 담아주어서
방정식 [10.3]에서 torque in world coordinates와 계산하기만 하면된다.
그런데, inertia tensor를 기저변환할 때, 우리는 position이 아닌 rotation에만 관심이 있다. 그래서 기저변환에 쓰이는 T행렬은 rotation components만 담기는 mat3 타입이 된다.
따라서 Rigid Body는 다음의 계산을 하게 된다.
1. Transform Matrix from Position and Orientation
2. Inverse Inertia Tensor world From Orientation of Transform Matrix
3. Rigid Body Integration
- D'Alembert for Rotation
Force 때 처럼, Rotation도 마찬가지로 합을 통해 단일의 torque로 바꿀 수 있다.
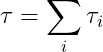
- Force generator + torque generator
구현 관련. 책 참고.
- Rigid Body Intergration
구현 관련, 책 참고. 앞에서 이미 공부한 내용임.
10.1을 보면 f와 p_f가 같은 방향이면 torque는 zero가 된다.
즉, force의 연장선이 CM을 지나면 어떤 torque도 없다.
- The Moment of Inertia (관성모멘트) : Rotational Equivalent of Mass. 오브젝트의 회전 속도를 바꾸기 얼마나 어려운지에 대한 척도이다.
Inertia Tensor(Tensor는 어떤 차원의 배열인데, Rigid Body Physics에서는 항상 2x2이므로, Matrix 라고 봐도 무방하다) : 여러 축에 대한 관성모멘트를 표현한다.
I_x,y,z : CM을 통해 그것의 각 축에 대해 그 오브젝트의 관성모멘트
나머지 항들은 products of inertia라고 불려진다.
{
https://youtu.be/a9n2Ztp1Oic
https://www.youtube.com/watch?v=mFVz7iCc45I
https://www.youtube.com/watch?v=M_S4neYZ7CM
Rigid Body의 Inertia Tensor에 대한 유튜브 강의 들이 있다.
Inertia Tensor가 뭐하는 개념인지는 대충 아니까
그것의 유도를 나중에 시간날 때 들으면 좋을 것 같다.
}
그래서 Rigid Body에서 Torque를 구하는 식은 이 tensor를 이용하여
이렇게 되고, 우리가 알고싶은 Angular Acceleration은
그런데 위에 식에서, torque와 angular acceleration은 world coordinates에 있는데,
보통 Inertia tensor는 object의 local coordinates를 기준으로 두고 있다. 따라서, 우리는
inertia tensor in world coordinates를 구할 필요가 있다. 이 때 chapter 9에서 나온 기저변환을 사용한다.
좀 더 직관적으로 보여주자면
이런식으로 구성되고, T^-1은 transpose를 통해 연산량을 줄인다.
I^world라는 저렇게 계산된 inertia tensor world가 있다면, world 좌표계의 벡터 그러니까
우리의 목적인 torque in world coordinates와 I^world가 곱해진다고 해보자.
그러면 T^-1을 통해 우선적으로 torque은 local coordinates로 들어가게 되고,
torque in local coordinates는 I^Body와 같은 space에서 계산되어진다, 그렇게 계산되고난 후 다시 T를 통해 world 좌표계로 돌려지는 것이다.
이러한 과정이 I^world에 담겨있으므로, 우리는 기저변환하여 I^world에 담아주어서
방정식 [10.3]에서 torque in world coordinates와 계산하기만 하면된다.
그런데, inertia tensor를 기저변환할 때, 우리는 position이 아닌 rotation에만 관심이 있다. 그래서 기저변환에 쓰이는 T행렬은 rotation components만 담기는 mat3 타입이 된다.
따라서 Rigid Body는 다음의 계산을 하게 된다.
1. Transform Matrix from Position and Orientation
2. Inverse Inertia Tensor world From Orientation of Transform Matrix
3. Rigid Body Integration
- D'Alembert for Rotation
Force 때 처럼, Rotation도 마찬가지로 합을 통해 단일의 torque로 바꿀 수 있다.
- Force generator + torque generator
구현 관련. 책 참고.
- Rigid Body Intergration
구현 관련, 책 참고. 앞에서 이미 공부한 내용임.
Chris Hecker Article 4
이 자료는 2D Rigid Body Physics 에서 3D Rigid Body Physics로 넘어가서 설명한다. 2D와 유도하는 흐름이 비슷하고, Angular Effects에 대해서 더 많은 수학들이 쓰인다. 여기에서는 방향을 나타낼 때 Quaternion을 사용하지 않고 Matrix로 나타낸다.
- 2D -> 3D Kinematics
우선, 벡터를 두 개의 elements에서 세 개의 elements로 증가시킨다. 이것은 매우 간단하고, 뭐 특별할 게 없다.
하지만 방향을 나타낼 때 여러가지 신경쓸 게 있는데,
방향은 3차원에서 세 개의 자유도를 갖는다.
글쓴이는, 자유도에 이야기 하면서 다음의 원리에 대해서 간단히 명시한다.
"제약없는 자유도의 원래 개수" - "스칼라 제약 방정식의 개수" = "최종 자유도의 개수"
이 공식은 GPED의 책에서 회전에 대해 설명할 때 보았던 것과 같다. 아마 GPED의 글쓴이는 Chris Hecker가 설명한 부분을 썼을 것이다.
Chris Hecker는 3x3 회전행렬에 대해서 자유도의 관점에서 설명한다.
3x3 matrix는 9개의 DOF(Degrees of Freedom, 자유도)를 가지며,
"Special Orthogonal"이라는 제약을 가져서 방향을 나타낸다고 한다.
"Special" -> 행렬이 Reflection이 아니다 -> 오른손 좌표계 왼손 좌표계로 바꿀 수 없다.
{
행렬이 reflection이 아니라는게 정확히 무엇인지 모르겠다.
글쓴이가 그 뜻이, 오른손 왼손 좌표계로 바꿀 수 없다는데, 방향을 나타내는 것의 z축 방햔만바꾸면 좌표계를 바꿀 수 있을텐데..
나중에 더 알아보아야 겠다.
}
"Orthogonal" ->
=> 대각선 성분이 1 (3개의 제약), 나머지가 0인데 서로 직교하개 한다 (3개의 제약)
그러나, Numerically하게 정확도의 문제가 있긴하다.
- Chris Hecker도 여기에서 기저변환을 설명했으나, 위에서 관련자료와 언급을 했기에 여기서는 넘어간다.
- Axis and Angle
이 파트는 3차원에서 어떤 벡터를 회전시키는 것에 대해 알려주는 파트이다. 특히, 위에서 링크시켜놓은 Rodrigues' Formula를 더 간단하게 설명해놓았다.
Axis는 3DOF이고, Angle은 1DOF이기에, 총 4개의 DOF에서, 그 Axis 벡터가 단위 길이가 되도록 하는 제약에 총 3개의 DOF를 갖게되므로, 방향을 나타내는데 쓸 수 있다.
이 부분은 Chris Hecker 자료 4에 있는 그림과 설명을 보면서 공부하는게 더 좋을 것이다.
Chris Hecker에 따라,
3차원에서 어떤 회전축 n(단위 벡터)에 따라 theta만큼 회전 시켰을 때, 그것을 간단하게 표현하자면
다음과 같이 식이 표현된다. 이제 o, x, y벡터 각각에 대한 설명을 할 필요가 있다.
o는 rodrigues의 공식에서는 회전축에 평행인 벡터와 같다.
그래서 처음에 n^T * r을 통해 내적을 한 후 (이것은 r을 n에 사영시키는 것이다 n이 단위벡터이기에 r이 n에 사영될 때의 길이가 나온다), 거기에 다시 n벡터를 곱해서, n의 방향을 ㅏ갖게 한다. 그래서 o는 회전축에 평행한 벡터이다.
로드리게즈 공식에서 말하듯이, 회전축에 평행한 벡터는 움직이지 않고, 수직인 벡터만 움직인다. 좀 더 쉽게 Chris Hecker의 자료를 통해 설명하자면
우리는 벡터 r의 끝점이 회전할 때 만드는 평면을 생각해 본다면된다. 그래서 벡터 r의 끝점이 가리키는 곧이, 원점 o에서 x축 방향이 이 되게 하는 것이다.
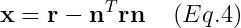
그래서 벡터로 치자면 r - o이므로 o에서 r로 가는 벡터가 된다. 여기에서 x방향 벡터를 표준화 하지 않는 이유는, 처음 나온 위의 r'식에서 r길이를 유지해야하기 때문이다.
그리고 이제 y벡터를 구해야 하는데, 이 y벡터라는 것은 n과 x방향에 수직이여야 한다. 근데 생각해 본다면, x는 n과 r의 평면위에서 표현되는 것이기 때문에, y벡터는 n과 r벡터에 수직이여야 한다. 따라서,
그러므로,
이런식이 최종적으로 나오게 된다, 로드리게스 공식과 똑같이 바꿔주자면 (공통된 항을 통해 정리해준다),
다음처럼 바뀐다.
그래서 위의 것을 행렬의 형태로 표현한다면
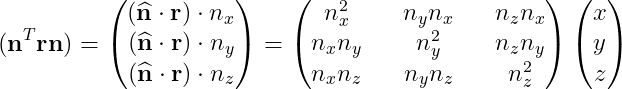
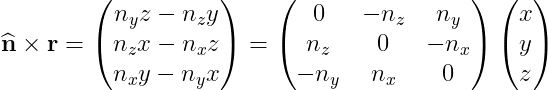
이런식으로 표현되어서 최종 로드리게스 행렬 공식이 나오게 된다.
- 2D -> 3D Kinematics
우선, 벡터를 두 개의 elements에서 세 개의 elements로 증가시킨다. 이것은 매우 간단하고, 뭐 특별할 게 없다.
하지만 방향을 나타낼 때 여러가지 신경쓸 게 있는데,
방향은 3차원에서 세 개의 자유도를 갖는다.
글쓴이는, 자유도에 이야기 하면서 다음의 원리에 대해서 간단히 명시한다.
"제약없는 자유도의 원래 개수" - "스칼라 제약 방정식의 개수" = "최종 자유도의 개수"
이 공식은 GPED의 책에서 회전에 대해 설명할 때 보았던 것과 같다. 아마 GPED의 글쓴이는 Chris Hecker가 설명한 부분을 썼을 것이다.
Chris Hecker는 3x3 회전행렬에 대해서 자유도의 관점에서 설명한다.
3x3 matrix는 9개의 DOF(Degrees of Freedom, 자유도)를 가지며,
"Special Orthogonal"이라는 제약을 가져서 방향을 나타낸다고 한다.
"Special" -> 행렬이 Reflection이 아니다 -> 오른손 좌표계 왼손 좌표계로 바꿀 수 없다.
{
행렬이 reflection이 아니라는게 정확히 무엇인지 모르겠다.
글쓴이가 그 뜻이, 오른손 왼손 좌표계로 바꿀 수 없다는데, 방향을 나타내는 것의 z축 방햔만바꾸면 좌표계를 바꿀 수 있을텐데..
나중에 더 알아보아야 겠다.
}
"Orthogonal" ->
그러나, Numerically하게 정확도의 문제가 있긴하다.
- Chris Hecker도 여기에서 기저변환을 설명했으나, 위에서 관련자료와 언급을 했기에 여기서는 넘어간다.
- Axis and Angle
이 파트는 3차원에서 어떤 벡터를 회전시키는 것에 대해 알려주는 파트이다. 특히, 위에서 링크시켜놓은 Rodrigues' Formula를 더 간단하게 설명해놓았다.
Axis는 3DOF이고, Angle은 1DOF이기에, 총 4개의 DOF에서, 그 Axis 벡터가 단위 길이가 되도록 하는 제약에 총 3개의 DOF를 갖게되므로, 방향을 나타내는데 쓸 수 있다.
이 부분은 Chris Hecker 자료 4에 있는 그림과 설명을 보면서 공부하는게 더 좋을 것이다.
Chris Hecker에 따라,
3차원에서 어떤 회전축 n(단위 벡터)에 따라 theta만큼 회전 시켰을 때, 그것을 간단하게 표현하자면
다음과 같이 식이 표현된다. 이제 o, x, y벡터 각각에 대한 설명을 할 필요가 있다.
o는 rodrigues의 공식에서는 회전축에 평행인 벡터와 같다.
그래서 처음에 n^T * r을 통해 내적을 한 후 (이것은 r을 n에 사영시키는 것이다 n이 단위벡터이기에 r이 n에 사영될 때의 길이가 나온다), 거기에 다시 n벡터를 곱해서, n의 방향을 ㅏ갖게 한다. 그래서 o는 회전축에 평행한 벡터이다.
로드리게즈 공식에서 말하듯이, 회전축에 평행한 벡터는 움직이지 않고, 수직인 벡터만 움직인다. 좀 더 쉽게 Chris Hecker의 자료를 통해 설명하자면
우리는 벡터 r의 끝점이 회전할 때 만드는 평면을 생각해 본다면된다. 그래서 벡터 r의 끝점이 가리키는 곧이, 원점 o에서 x축 방향이 이 되게 하는 것이다.
그래서 벡터로 치자면 r - o이므로 o에서 r로 가는 벡터가 된다. 여기에서 x방향 벡터를 표준화 하지 않는 이유는, 처음 나온 위의 r'식에서 r길이를 유지해야하기 때문이다.
그리고 이제 y벡터를 구해야 하는데, 이 y벡터라는 것은 n과 x방향에 수직이여야 한다. 근데 생각해 본다면, x는 n과 r의 평면위에서 표현되는 것이기 때문에, y벡터는 n과 r벡터에 수직이여야 한다. 따라서,
그러므로,
이런식이 최종적으로 나오게 된다, 로드리게스 공식과 똑같이 바꿔주자면 (공통된 항을 통해 정리해준다),
다음처럼 바뀐다.
그래서 위의 것을 행렬의 형태로 표현한다면
이런식으로 표현되어서 최종 로드리게스 행렬 공식이 나오게 된다.
- Angular Velocity
이전 섹션으로 부터 이제 한 벡터가 회전축 n에 대해 𝛉만큼 회전하고 나서의 상황을 알 수 있다.
그 전에 우리는 회전하고 있는 벡터의 변화량을 알고 싶은데, 2D article과 비슷하게 유도한다.
Chris Hecker Article 2의 2D에서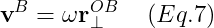 를 증명하기 위해 길이와 방향에 대해 증명을 했었다. 그 길이는 r * theta의 변화량이 였는데 3D에서
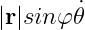
이전 섹션으로 부터 이제 한 벡터가 회전축 n에 대해 𝛉만큼 회전하고 나서의 상황을 알 수 있다.
그 전에 우리는 회전하고 있는 벡터의 변화량을 알고 싶은데, 2D article과 비슷하게 유도한다.
Chris Hecker Article 2의 2D에서
가 된다. 여기에서 |r|sinpi를 통해, 그림에서 x축의 길이가 (즉, 반지름 길이) 구해지고, theta의 변화량 만큼해서 그 position의 변화량이 구해지는 것이다.
그리고 방향에 대해서, 위에서 언급했듯이, n과 r의 벡터가 만드는 평면에 수직해야 한다. 즉, n과 r에 둘 다 수직해야 한다.
결과적으로,
만약 angular velocity를 회전축 * 회전 속력으로 정의한다면, 우리는 이제 2D에서와 비슷한 공식을 얻게 된다. 이 Eq.7은 r이 constant vector(변하지 않은 상수 벡터) 여야 유효하다. 즉, r의 길이를 바꾸어서는 안된다.
이것을 수적으로 다르게 미분하여 구하는 방법이 또 있다.
이전 섹션에서 구한 Eq.6을 미분해보면
이렇게 된다. 그리고 \theta가 0이라고 한다면 sin\theta = 0이고, cos\theta = 1이고,
우리는 Eq.7만을 가지게된다. 여기에서 \theta가 0이라고해서 dot(\theta) (즉, theta의 변화량)이 0은 아니다.
우리는 이제 Angular Velocity 𝞈 벡터에 대한 표기를 가지게 되었고, 이것은 순간의 시간에 적분할 때 쓰이는 양일 뿐이다. 그래서 그 이전과 그 이후 어떤 순간에도 쓰이면 안되고 그 순간에만 쓰여야 하는 것이다.
여기까지 온 이유는, 3차원 Orientation을 표기하는 방법을 로드리게스 공식을 통해서 표기하고, 우리는 적분을 통해서 그 Orientation을 계속 유지하는데, 이제 적분을 함으로써, 그 Orientation을 Angular Velocity를 통해 변화시켜야 하기 때문이다. 즉, Orientation Matrix를 미분을 어떻게 하냐는 것이다.
우리는 방정식 7을 다시 보아야 하는데, 한 column vector(r)을 "미분하는" Angular Velocity Vector를 보게 된다. 그래서 우리는 각 Orientation Matrix의 Column을 미분하는 Angular Velocity를 쓰게 될 것이다. 이 때 우리는 한 Column에 대해 하나씩 외적을 하여서 방향 행렬을 구성할 수도 있지만, tilde operator 또는 Skew Symmetirc Matrix라고 불리는 것을 구성하여 좀 더 우아하게 이것을 할 수 있다.
따라서 Orientation Matrix A라 한다면,
이제 이걸로 우리는 Angular Velocity로부터 적분하여 Orientation의 변화량을 얻어서 Orientation을 설정할 수 있다.
{
Chris Hecker는 Orientation Matrix로 이것을 설명헀지만, GPED책과 이 다음의 David Baraff 논문에서는 Quaternion을 통해 했다. 어쨋든 이러한 설명도 보는 것도 유익하다.
}
- 움직이는 body에서의 한 점에 대한 kinematic equations
이제 우리가 얻은 것을가지고, kinematic equations를 볼 것이다. 이 섹션도 자료에 있는 그림을 참고하면서 공부하는 것이 좋을것이다. 이 파트는 앞의 Angular Velocity를 이용하여 Kinematic Quantities 사이의 관계를 알아보는 것에 그친다. 실제로 시뮬레이션에서 사용되지 않는다.
점 b 벡터 = o + ob = o + r
점 b 벡터 = o + ob = o + r
body의 origin o를 통해 표현될 수 있다.
이제 body가 회전을 하고 있다 했을 때, bar(r)이 body space에서 표기된 것이라고 한다면
라고 표기될 수 있다. 즉, Body Space에 있는 bar(r)이 A 방향으로 회전되어서 올바른 위치로 지금 표기되고 있는 것이다.
이제 Eq.11을 미분하여 b의 속도를 얻어보자. 두 가지 방법이 있는데 먼저 간단한, o + r을 미분해보자.
이제 body가 회전을 하고 있다 했을 때, bar(r)이 body space에서 표기된 것이라고 한다면
라고 표기될 수 있다. 즉, Body Space에 있는 bar(r)이 A 방향으로 회전되어서 올바른 위치로 지금 표기되고 있는 것이다.
이제 Eq.11을 미분하여 b의 속도를 얻어보자. 두 가지 방법이 있는데 먼저 간단한, o + r을 미분해보자.
Eq.7에 의해 dot(r) 은 omega X r이 되었다.
다음으로 o + Abar(r)을 미분의 곱 법칙에 의해 미분해보자.
bar(r)는 body에 있는 constant vector이기 때문에, 그것의 시간에 대한 미분은 0이 된다. 우리는 또한 Eq.10을 이 방정식에 넣을 수 있는데, 그래서 다음을 얻게 된다.
결국에는 같은 속도에 대한 방정식을 얻게 되는 것이다.
이제 한 번더 미분하여 b의 가속도를 얻어보자.
{
나는 여기에서 dot(b)의 미분이 왜 저렇게 되는지 모르겠다.
}
여기에서 세 번째 항은 물리학에서 구심력을(centripetal accleration) 가리킨다고 한다. 이 구심력은 body의 origin뒤 쪽으로 향하고 있다고 한다.
- 3D Dynamics
이제 이전처럼 CM, Kinematics와 Dynamics Quantity 사이의 관계식을 찾으러 갈 시간이다.
먼저 CM의 유도는 이전과 똑같으므로 글쓴이도 그냥 방정식으로 표현해버린다고 했다.
이제 Force에 대해서는 그냥 간단하다. 이전과 같다. 하지만, Angular Momentum은 조금 달라진다.
3D Angular Momentum은 회전축이 필요하고 이제 Angular Momentum L은 vector representation이 된다. 어떤 점 A에 대한 점 B의 회전은 2D에서 perp-dot product로 scalar였는데, 3D에서 A에 대해 회전하는 B의 linear momentum의 양이 얼마나 있는지가 된다. 그래서, Angular Momentum은 외적이 필요한데, 그 이유는 A에 대해 회전하는 운동량의 평면을 묘사하는 벡터가 필요하기 때문이다. 이것은 아까 로드리게스 공식과 같은 것을 유도하는 도중에 y = n x r를 구할 때와 같은 의미이다.
그리고 2D에서 처럼 Angular Momentum의 미분은 이제 Torque가 된다.
Torque는 주어진 점이 겪는 회전력의 양을 측정한다.
이제 이러한 양의 "total" version을 구해야 한다.
맨 오른쪽에 식을 약간 변형해서 r의 미분을 써놨는데, 이렇게 한 이유는 이제야 angular dynamic quantities와 angular kinematic quantities를 연결시키기 위해서이다.
이제 Eq .7을 대신해서 넣는다
이전에 외적연산을 tilde 표현으로 했듯이 그렇게 바꿔준다. 그리고 omega(angular velocity)는 한 body에 대해 instant time에 상수이니까 sigma 식에서 빠져 나오게 된다.
그리고 이제 우리는 Inertia Tensor를 만나게 되는 것이다.이것은 body의 angular velocity와 angular momentum을 연관시키게 된다. inertia tensor는 회전할 때 마다 바뀌는데 world-space r에 의존하기 때문이다. 이 때 CM에 의존하게 되면 쉽게 total torque까지 구할 수 있다.
그리고 우리가 world space inertia tensor를 안다고 한다면, body에 대한 angular velocity를 알 수 있게 된다.
- Inertia Tensor
좀 더 글이 길긴하지만, 이것을 최대한 간단하게 설명하고자 한다.
Inertia Tensor는 회전할 때 마다 바뀌는데, 우리가 Body Space에서 Inertia Tensor를 적용하고, 그 Body의 Transform Matrix를 통해 Inertia Tensor in World Space를 구할 수 있다면은 언제든 원하는 Inertia Tensor를 적용시킬 수 있다. 왜냐하면
이것이기 때문에 bar(r)들은 고정된 상수이기 때문이다 (Rigid Body는 모양이 변하지 않기에). 따라서, Body Space에서 Inertia Tensor를 설정하고 기저 변환을 통해 world를 구하면 된다.
좀 더 연산에 유리하게 한다면 inverse inertia tensor를 구하도록 하는게 좋다. 그래서
이런식으로, inverse inertia tensor world를 구할 수 있게 된다.
여기에서 우리가 모르는 것은 body-space inertia tensor를 구하는 건데, 방정식 19가 보여주듯이 우리는 body의 부피에 대해 적분을 수행해야 한다. 또는 이상한 모양의 bodies에 대해 좀 더 복잡한 적분을 하게 된다. 간단한 도형에 대해 inertia tensor에 대한 표가 있기도 해서 그것을 참고해도 되고, 복잡한 도형은 거의 옳게 행동하도록 근사를 시키거나, 아니면 아까 말한 복잡한 적분을 해야한다.
- 3D Dynamics Algorithm
여러 방정식을 만났으니 이제 최종 알고리즘 전반을 봐야한다. 여기에서는 Collision Detection and Response가 없다.
* 초기화
Body Constants 결정 : Inverse Inertia Tensor in Body Space, Total Mass
Initial Conditions 결정 : r_CM, v_CM, A(방향), L^_CM(angular momentum)
Intial auxiliary quantities 결정 :
inverse inertia Tensor in world space = A bar(I)^-1_CM A^T
angular velocity = inverse inertia tensor in world space * Total angular Momentum
* Simulation
1) 개별 Forces와 적용점 계산 : F_i, r_i
2) total forces와 torques 계산
3) 적분 :
1. 속도를 적분하여 새로운 위치 얻기
2. 총 Force에 대해 Mass를 나누어서, 가속도 a를 얻은 후
h만큼 스케일링해 가속도를 적분하여 새로운 속도 얻기
3. Angular Velocity로 이전 Orientation을 미분시켜서 변화량을 얻은 후,
h만큼 스케일링 해 Angular Velocity를 적분하여 새로운 Orientation 얻기
4. Total Torque에 h만큼 곱하여 다음의 Angular Velocity를 위한 Angular Acceleration를 적분할 것을 얻기 위한 준비.
4) Auxiliary Quantities 연산
1. 새로운 방향에 대해 Inverse Inertia Tensor World 연산
2. 그 얻어진 새로운 Inverse Inertia Tensor World를 통해, 이전에 torque * time step에 곱하여 새로운 angular velocity로 적분하여 angular velocity를 설정함.
- 이후
글쓴이는 3D Collision Response는 Article 3에서 2D 버전을 3D 버전으로 바꾸면 된다고 한다. 그래서 주의할 점을 알려주고 최종적으로 j를 구하는 식을 알려준다.
그리고, 이후에도 구현할 여러가지 것들에 대해서도 알려준다.
An Introduction to Physically Based Modeling : Rigid Body Simulation 1 - Unconstrained Rigid Body Dynamics (David Baraff)
이 논문은 이제 처음 보는 것이기 때문에, 그냥 번역하면서 공부한다. 지금 번역하기 전에 훑어 보니, 위에서 설명한 것과 반복되는 것이 있기 때문에 좀 더 간략화 하면서 지나갈 수도 있다.
Introduction
이 과목의 이 부분은 Rigid Body Dynamics의 문제를 다룬다. Rigid Body Motion을 재현하는 것을 시작하는 것을 돕기 위해, 우리는 이러한 notes들에서 이야기되는 대부분의 개념들을 구현하는 code fragments를 제공한다. 그 course notes의 이 segment는 두 개의 부분으로 나눠진다. 그 첫 번째 파트는 그것들의 허용될 수 있는 움직임에서 완전히 unconstrained(제약 받지 않는) rigid bodies의 움직임을다룬다; 즉, rigid bodies 사이의 충돌에 대한 관련이 없는 simulation이다. 어떤 외부의 forces가 주어진다면, 우리는 이러한 forces에 대응하여 그 body의 움직임을 어떻게 재현할지를 보여줄 것이다. 이러한 notes에서 수학적 유도는 꽤 공식적이고(informal) 직관적이 되도록 의도된다.
그 notes의 두 번째 부분은 우리가 bodies를 solid라고 간주할 때, 그리고 inter-penetration을 허용하지 않을 필요가 있을 때 발생하는 constrained motion의 문제를 다룬다. 우리는 접촉하는 bodies 사이의 적절한 contact forces를 연산하여, 이러한 non-penetration constraints (관통하는 것이 없는 제약) 를 실행한다. 이러한 contact forces에 대한 값이 주어진다면, unconstrained case에서 처럼 정확히 시뮬레이션이 진행된다 : 우리는 모든 forces를 그 bodies에 적용하고, 그 시뮬레이션이 bodies의 움직임에 완전히 제약받지 않는 것처럼 진행되도록 한다. 만약 우리가 contact forces를 정확히 연산헀다면, 그 bodies의 최종 움직임은 inter-penetration으로부터 자유로울 것이다. 이러한 contact forces의 계산은 전체 시뮬레이션 프로세스에서 가장 까다로운 component이다.
Part 1. Unconstrained Rigid Body Dynamics
1 Simulation Basics
course notes의 이 부분은 rigid body motion의 완전한 구현을 위해서 맞춰진다. 이 섹션에서, 우리는 한 rigid body의 움직임을 재현하는 기본 구조를 보여줄 것이다. section 2에서, 우리는 rigid body simulator를 구현하는데 필요한 용어, 개념, 방정식들을 정의할 것이다. 이것을 따라서, 우리는 우리가 필요한 방정식을 실제로 구현하는 몇 가지 코드를 줄 것이다. 우리가 사용할 그 개념과 방정식에 대한 유도는 appendix A에 남겨질 것이다.
이 지점에서 너가 친숙해질 필요가 있는 유일한 것은 Ordinary Differential Equations를 해결하는 것의 기본 개념이다 (numerical details가 아닌). 만약 너가 이 주제에 익숙하지 않다면, 너는 운이 좋다 : 이 course notes의 처음에로 돌아가서, "Differential Equation Basics" 섹션을 읽어라. 너는 또한 "Particle Dynamics"의 다음 섹션을 읽길 원할지도 모른다. 비록 우리가 여기에서 그 자료의 몇 가지를 반복하려고 할지라도.
rigid body의 움직임을 재현하는 것은 거의 파티클의 움직임을 재현하는 것과 같다. 그래서 파티클 시뮬레이션으로 시작하자. .... 생략 ...
2 Rigid Body Concepts
이 섹션의 목표는 rigid bodies에 대해 방정식 (1-3)과 유사한 것을 개발하는 거싱다. 우리가 개발할 최종 미분방정식은 section 2.11에서 주어진다. 이것을 하기 위해서, 우리는 처음에 많은 개념들을 정의하고 관계들을 정의할 필요가 있다. 더 긴 유도들 몇 가지는 appendix A에 있다. 다음 섹션에서, 우리는 이 섹션에서 개발된 X(t)의 미분을 연산하기위해 numerical solver ode에 필요한 함수 Dxdt()를 어떻게 작성하는지를 보여줄 것이다.
2.1 Position and Orientation
.... rigid body를 world space에서 위치시키기 위해, 우리는 x(t)라는 벡터를 사용할 것인데, 이것은 그 body의 평행이동을 묘사한다. 우리는 또한 그 body의 회전을 묘사해야만 하는데, 우리는 그것을 3x3 rotation matrix R(t)의 관점에서 할 것이다. 우리는 x(t)와 R(t)를 한 rigid body의 spatial variables라고 부를 것이다.
파티클과 다르게, 한 rigid body는 공간의 한 부피를 차지하고, 특별한 모양을 갖는다. 한 rigid body는 오직 회전과 평행이동만을 겪을 수 있기 때문에, 우리는 body space라고 불려지는 고정되고 불변하는 공간에서의 관점에서 rigid body의 모양을 정의할 수 있다. body space에서 body의 기하학적 묘사가 주어진다면, 우리는 body-space description을 world space로 transform하기위해 x(t)와 R(t)를 사용한다. 우리가 사용할 몇 가지 방정식을 간단하게 하기 위해, 우리는 body space에서 rigidbody의 우리의 묘사가 body의 center of mass가 원점 (0,0,0)에 있도록 요구한다. 우리는 CM을 좀 더 정확히 나중에 정의할 것이지만, CM은 그 body의 기하학적 중심에 놓여있는 rigid body의 한 점으로 생각되어질 수 있다. body의 shape를 묘사할 때, 우리는 이 geometric center가 body space에서 (0,0,0)에 있도록 요구한다. 만약 우리가 R(t)가 center of mass에 대한 body의 회전을 명시하는 것을 동의한다면, body space에 있는 한 고정된 벡터 r은 time t에 R(t) * r의 world space 벡터로 회전될 것이다. 마찬 가지로, p_0은 body space에서 rigid body의 임의의 점이라고 한다면, 그러면 p_0의 world-space location p(t)는 원점에 대해 p_0을 먼저회전 시키고나서, 그것을 평행이동 시킨 결과가 될 것이다
p(t) = R(t)p_0 + x(t). (2-1)
body의 CM이 원점에 놓여있기 때문에, CM의 world-space location은 항상 x(t)에 의해서 직접적으로 주어진다. 이것은 x(t)가 time t에 world space에 있는 CM의 위치라는 것을 말하여서 x(t)에 대한 물리적인 의미를 붙이도록 해준다. 우리는 또한 R(t)에 물리적인 의미를 붙일 수 있다. 즉, body space에서 x축이 vector (1, 0, 0)이라고 고려하자. time t에서, 이 벡터는 world space에서 다음의 방향을 갖는다.
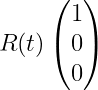
만약 우리가 R(t)의 컴포넌트들을 다음과 같이 쓴다면
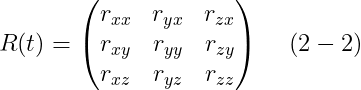
그러면
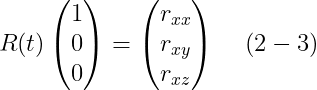
가 되고, 이것은 R(t)의 첫 번째 열이다. R(t)의 물리적인 의미는, time t에 world space로 변환될 때 R(t)의 첫 번째 열은 rigid body의 x축이 가리키는 방향을 준다는 것이다. 유사하게, R(t)의 두 번째와 세번째 열들도 time t에 world space에서 rigid body의 y와 z축들의 방향을 준다.
2.2 Linear Velocity
간단함을 위해서, 우리는 x(t)와 R(t)를 time t에서 body의 position과 orientation이라고 부를것이다. 다음으로 우리가 할 필요가 있는 것은 시간에 대해 position과 orientation이 어떻게 변하는지를 정의하는 것이다. 이것은 우리가 dot(x)(t)와 dot(R)(t)에 대한 표현이 필요하다는 것을 의미한다. x(t)가 world space에서 CM의 위치이기 때문에, dot(x)(t)는 world space의 CM의 velocity가 된다. 우리는 linear velocity v(t)를 이 속도로 정의할 것이다:
v(t) = dot(x)(t) (2-4)
만약 우리가 body의 orientation이 고정되어있다고 상상한다면, 그러면 그 body가 격을 쑤 있는 유일한 움직임은 순수한 평행이동이다. 그 v(t) 양은 이 translation의 속도를 준다.
2.3 Angular Velocity
평행이동 하는 것 외에도, rigid body는 또한 회전할 수 있다. 우리가 CM의 위치가 공간에서 움직일 수 없게 했다고 상상해라. 그 몸의 점들의 어떤 움직임은 그러므로 그 body에 의해 CM을 지나는 어떤 축에 대해 회전해야만 한다. (그렇지 않다면 그 CM자체만 회전할 것이다). 우리는 그 spin을 한 벡터 𝞈(t) 로 묘사할 수 있다. 𝞈(t)의 방향은 그 body가 회전하고 있는 축의 방향을 준다 (그림 3). 𝞈(t)의 크기, |𝞈(t)|는 그 body가 얼마나 빠르게 회전하고 있는지를 말한다. |𝞈(t)|는 revolutions/time의 관점을 가지고 있다; 따라서 |𝞈(t)|는 그 body가 주어진 시간 동안 회전할 angle과 연관짓는다, 만약 그 angular velocity가 변하지 않는다면. 그 quantity 𝞈(t)는 angular velocity라고 불려진다.
linear velocity에 대해, x(t)와 v(t)는 v(t) = d/dt x(t)와 연관된다. R(t)와 𝞈(t)는 어떻게 연관되는 가? (명백히, dot(R)(t)는 w(t)가 될 수 없다, 왜냐하면 R(t)가 행렬이고 w(t)는 벡터이기 때문이다.) 이 질문에 답하기 위해서, 우리는 R(t)의 물리적인 의미를 상기하도록 하자. 우리는R(t)의 columns들이 우리에게 time t에서 변환된 x, y and z body axes의 방향을 말해준 다는 것을 안다. w(t)와 R(t) 사이의 관계를 발견하기 위해, rigid body에서 임의의 벡터가 angular velocity 𝞈(t)와 어떻게 연관되는지를 시험해보자.
그림 4는 angular velocity 𝞈(t)를 가진 rigid body를 보여준다. world space에서 명시된 time t 에서의 한 벡터 r(t)를 고려해라. 우리가 이 벡터가 그 body에 고정되어 있다고 고려한다고 가정하자; 즉, r(t)는 world space를 통해 그 rigid body와 함께 움직인다. r(t)는 한 방향이기 때문에, 그것은 어떤 평행이동 효과와 무관하다; 특히, dot(r)(t)는 v(t)와 독립적이다. dot(r)(t)를 공부하기 위해서, 우리는 r(t)를 벡터 a와 b로 분해하는데, a는 w(t)와 평행하고, b는 w(t)와 수직이다. rigid body가 constant angular velocity를유지한다는 것을 가정하자, r(t) 벡터의 끝이 instantaneously하게 이 원을 따라 움직이기 때문에, r(t)의 instantaneous change는 b와 w(t) 둘 다에 수직이다. r(t)의 tip이 반지름이 b인 한 원에서 움직이고 있기 때문에, r(t)의 instantaneous velocity는 |b||w(t)|의 크기를 갖는다.
b와 w(t)가 수직이기 때문에 그것들의 외적은 그 크기를 갖는다
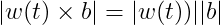(2-5)
이 것을 합하여, 우리는 dot(r)(t) = w(t) X (b) 라고 쓸 수 있다. 그러나, r(t) = a + b이고, a는 w(t)에 평행하기 때문에, 우리는 w(t) X a = 0을 갖는다 따라서
(2-6)
따라서, 우리는 간단히 한 벡터의 변화율을 간단히 다음으로 표현할 수 있다
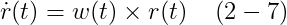
이것은 이제 모두 합쳐보자. time t에서, 우리는 world space에서 rigid body의 x 축의 방향이 [ r_xx r_xy r_xz ] 인 것을 알고,
time t에서 R(t)의 첫 번째 column의 미분이 이 벡터의 변화율이라는 것을안다: 우리가 발견한 외적 법칙을 사용하여 이 변화는
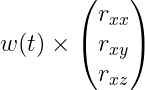
그 같은 것이 명백히 R(t)의 다른 두 개의 열들에도 유효하다. 이것은 우리가 다음을 쓸 수 있게 한다.
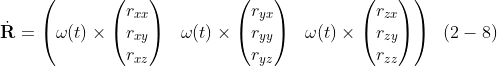
이것은 가지고 다니기에 너무 번거로운 수식이다. 간단하게 하기 위해서, 우리는 다음의 trick을 사용한다. 만약 a와 b가 3-vectors라면, 그러면 a x b는 다음의 벡터가 되고,
vector a가 주어진다면 a* 를 다음의 행렬이 되도록하자 (skew-symmetric matrix)
그러고나서,
a*b = a x b (2-9)
가 된다.
* notation을 사용하여, 우리는 dot(R)(t)를 좀 더 간단히 쓸 수 있다.
결국에 우리는 다음을 얻는다
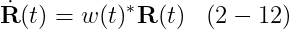
마지막으로, 이것은 우리에게 dot(R)(t)와 w(t) 사이에 원했던 관계를 준다.
한 벡터에 대해 dot(r)(t) = w(t) X r(t) 와 rotation matrix에 대해 dot(R)(t) = w(t)* R(t) 사이의 대응에 주목해라.
2.4 Mass of a Body
몇 가지 유도를 처리하기 위해서, 우리는 (개념적으로) 우리의 rigid body의 부피에 대해 어떤 적분을 수행할 필요가 있을 것이다. 이러한 유도를 더욱 간단하게 하기 위해, 우리는 일시적으로 한 rigid body가 수 많은 작은 파티클들로 구성되었다고 상상할 것이다. 그 파티클들은 1에서 N까지 인덱싱된다. i번째 파티클의 질량은 m_i이고, 각 파티클은 body space에서 r_0i의 (constant) 위치를 갖는다. time t에서 world space에 있는 i번째 파티클의 위치는 r_i(t)로 표기되고, 그러므로 다음의 공식에 의해 주어진다
그 body의 total mass, M은 다음의 합계이다
(이후로, 합계는 인덱스 변수 i로 1부터 N까지 합으로 가정된다.)
2.5 Velocity of a Particle
i번째 파티클의 velocity dot(r)_i(t)는 2-13 방정식을 미분하여 얻어진다: dot(R)(t) = w* R(t)의 관계를 사용하여 우리는 다음을 얻는다
우리는 이것을 다음으로 쓸 수 있다
방정식 2-13으로부터 r_i(t)의 정의를 사용해서. "*" operator의 정의로부터,
어떤 벡터 a에 대해 w(t) * a = w(t) X a라는 것을 회상해라. 이것을 사용하여, 우리는 간단히 쓸 수 있다
이것은 rigid body의 한 점의 velocity를 두 개의 컴포넌트로 분리한다 (그림 5) : linear component v(t)와 angular component w X (r_i(t) - x(t))
2.6 Center of Mass
CM의 우리의 정의는 마찬가지로 bodies의 dynamics를 linear and angular components로 분해할 수 있게 할 것이다. world space에서의 한 body의 CM은 다음으로 정의된다
여기에서 M은 그 body의 mass이다 (즉, 개별 질량 m_i의 합). 우리가 CM 좌표계를 사용한다고 말할 때, 우리는 BODY SPACE에서
를 의미하게 된다. (즉, CM이 원점이여야 한다는 것이다)
이것이 Sum(m_ir_0i) = 0 이라는 것을 또한 암시한다는 것에 주의해라.
우리는 x(t)가 time t에서 CM의 위치라고 말했었다. 이것은 사실인가? 그렇다: i번째 파티클은 time t에 position r_i(t) = R(t)r_0i + x(t)를 가지기 때문에, time t에서의 CM은
부가적으로
(2-20)
의 관계를 아는 것은 또한 중요하다.
2.7 Force and Torque
우리가 어떤 외부 영향 (예를들어, 중력, 바람, contact forces)에 의해 rigid body에 작용하는 한 force를 상상할 때, 우리는 그 force가 그 body의 한 특정한 particle에 작용한다고 상상할 수 있다. (우리의 파티클 모델을 개념적으로만 생각해라. 우리는 어떤 기하학적 위치에 한 force를 작용시킬 수 있고 또는 body안에 작용시킬 수 있다, 왜냐하면 우리는 항상 그 정확한 위치에서의 한 파티클이 있다고 상상할 수 있기 때문이다.) 그 force가 작용하는 particle의 위치는 그 force가 작용하는 위치를 정의한다. 우리는 F_i(t)가 time t에서 i번째 파티클에 작용하는 외부 forces로부터 온 total force라고 표기한다. 또한, 우리는 𝛕_i(t)를 i번째 파티클에 작용하는 external torque로 다음과 같이 정의한다
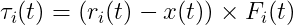(2-21)
한 파티클에서 Torque CM x(t)를 기준으로한 그 파티클의 r_i(t)의 위치에 의존한다는 점에서 force와 Torque는 다르다. 우리는 직관적으로 𝛕_i(t)의 방향을 body가 F_i(t)에 의해 회전하는 축이 된다고 생각할 수 있다, 만약 CM이 완전히 제자리에 있다면 (그림 6).
그 body에 작용하는 total external force F(t)는 F_i(t)의 합계이다:
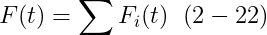
반면에 total torque는 유사하게 정의도니다
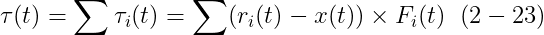
F(t)가 다양한 forces가 그 body에 어디에서 작용되었는지에 대한 정보를 전달하지 않는 것을 주목해라; 그러나 𝛕_(t)는 우리에게 body에 대한 forces F_i(t)의 distribution에 대한 어떤 것을 말해준다.
2.8 Linear Momentum
질량 m과 속도 v를 갖는 한 파티클의 linear momentum p는 다음으로 정의된다
한 rigid body의 total linear momentum P(t) 는 각 파티클의 mass and velocity의 곱의 합이다:
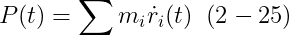
방정식 (2-17)로부터, i번째 파티클의 velocity dot(r)_i는
이고,
따라서, 그 body의 total linear momentum은
우리는 CM 좌표계를 사용하고 있기 때문에, 우리는 (2-20)방정식을 적용할 수 있고 다음을 얻을 수 있다
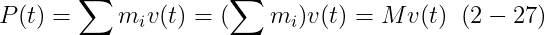
이것은 우리에게 우리의 rigid body의 total linear momentum이 그 body가 마치 질량 M과 속도 v(t)를 가진 하나의 파티클 처럼 같게 하는 좋은 결과를 준다. 이것 때문에, 우리는 P(t)와 v(t)사이의 간단한 변환을 갖는다: P(t) = Mv(t)와 v(t) = P(t) / M. M이 상수이기 때문에
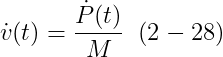
linear momentum의 개념은 우리가 꽤 간단하게 한 rigid body의 total force F(t)의 효과를 표현하게 해준다. Appendix A는 다음의 관계를 유도한다
그리고 이것은 linear momentum의 변화가 한 body에 작용하는 total force와 같은 것이라고 말한다. P(t)가 우리에게 한 body의 rotational velocity에 대해서 어떠한 것도 말하지 않는다는 것에 주목해라. 이것은 좋은 것이다. 왜냐하면 F(t)는 또한 한 body의 rotational velocity의 변화에 대해서도 어떠한 것도 전달하지 않기 때문이다!
P(t)와 v(t) 사이의 관계가 간단하기 때문에, 우리는 P(t)를 우리의 rigid body의 상태 변수로 사용할 것이다, v(t) 대신에. 우리는 v(t)가 물론 상태 변수가 되게 할 수 있고, 다음의 관계를 사용하게 할 수 있다.
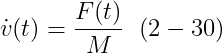
그러나, v(t) 대신에 P(t)를 상태 변수로 사용하는 것은 우리가 angular velocity와 acceleration을 다루는 방식과 좀 더 일관될 것이다.
2.9 Angular Momentum
linear momentum의 개념이 꽤 직관적인 반면에 (P(t) = Mv(t)), (rigid body에 대한) angular momentum의 개념은 그렇지 않다. 어떤 사람이 한 rigid body의 angular momentum에 시달리는 유일한 이유는, 만약 너가 angular velocity를 고수한다면 그것이 너가 얻는 것 보다 더욱 간단한 방정식을 쓰게 할 것이기 때문이다 - 그것은 가장 직관적이지 않은 개념이다. Angular momentum은 방정식을 결국에 간단하게 할 것이다. 왜냐하면 그것은 자연에서 그렇게 보존되기 때문이다, 반면에 angular velocity는 그렇지 않다: 만약 너가 body에 어떠한 torque도 작용하지 않는 공간을 통해 떠다니는 한 body를 갖는다면, 그 body의 angular momentum은 상수이다. 이것은 그런데 body의 angular velocity에 사실이 아니다: 비록 한 body의 angular momentum이 상수일지라도, 그 body의 angular velocity는 그렇지 않을 것이다! 결과적으로 한 body의 angular velocity는 어떠한 force가 body에 작용하지 않을 때에 변할 수 있다. 이것 때문에, angular momentum을 angular velocity보다 상태변수로 선택하는게 더 간단하게 된다.
linear momentum에 대해, 우리는 P(t) = Mv(t)의 관계를 갖는다. 유사하게, 우리는 rigid body의 total angular momentum L(t)를 다음의 방정식으로 정의한다 L(t) = I(t)w(t), 여기에서 I(t)는 inertia tensor이라고 불리는 우리가 곧 설명할 3x3 행렬이다 (기술적으로 rank-two tensor). 그 inertia tensor I(t)는 body에 있는 그 질량이 그 body의 CM을 기준으로 어떻게 분배되었는지를 묘사한다. 그 tensor I(t)는 한 body의 방향에 의존하지만, body의 평행이동에 의존하지 않는다. angular and linear case 둘 다에 대해, momentum은 velocity의 linear function 이라는 것을 주목해라 - angular case에서 scaling factor이고, 반면에 linear case에서 그것은 단순히 scalar이다. L(t)가 어떤 평행이동 효과와 독립적이라는 것에 주목해라, 반면에 P(t)는 어떠한 회전 효과와 독립이다.
L(t)와 𝞽(t)사이의 관계는 매우 간단하다: Appendix A는 다음을 유도한다
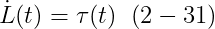
이것은 dot(P)(t) = F(t) 와의 관계와 유사하다.
2.10 The Inertia Tensor
그 inertia tensor I(t)는 angular momentum L(t)와 angular velocity 𝞈(t) 사이의 scaling factor이다. 주어진 시간 t에서, r'_i가 r'_i = r_i(t) - x(t)로 정의하여 x(t)로부터 i번째 파티클의 변위라고 하자. 그 tensor I(t)는 r'_i의 관점으로 대칭 행렬로 표현된다
(2-32)
실제 구현에 대해, 우리는 world space에서 한 body의 부피에 대해 적분으로 유한의 합을 대체한다. 그 질량 항 m_i는 density function으로 대체된다. 처음에 볼 떄, 우리는 방향 R(t)가 바뀔 때 마다 I(t)를 찾기 위해 이러한 적분을 할 필요가 있는 것처럼 보인다. 이것은 시뮬레이션동안 엄두를 못낼 만큼 하기에 비싸다. 만약 그 body의 shape가 너무 간단하지 않아서 그 적분이 symbolicaly하게 얻어질 수 있지 않다면.
운 좋게도, body-space coordinates를 사용하여, 우리는 body-space coordinates에서 미리 연산된 적분의 관점에서 값 싸게 어떤 방향 R(t)에 대한 inertia tensor를 연산할 수 있다. (이 적분은 일반적으로 시뮬레이션이 시작되기 전에 연산되고, body의 물리적 특성을 묘사하는 그 입력 파라미터들 중 하나로 간주되어질 것이다.) r'^T_i r'_i = r'^2_ix + r'^2_iy + r'^2_iz라는 사실을 사용하여, 우리는 I(t)를 뺄셈으로 다시 쓸 수 있다
(2-33)
r'_i 자기 자신괴 외적곱을 취하여, 즉
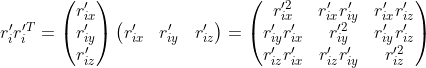(2-34)
l은 3x3 identity matrix를 나타내게 하여, 우리는 I(t)를 간단히 다음으로 표기한다
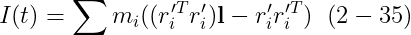
이것이 어떻게 도움이 되는가?
r_i(t) = R(t)r_0i + x(t) 이기에, r_0i는 상수이고, r'_i = R(t)r_0i 이다. 그러므로, R(t)R(t)^T = l이기 떄문에
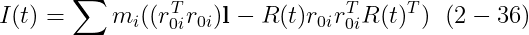
r^T_0i r_0i는 scalar이기 때문에, 우리는 다시 쓸 수 있다
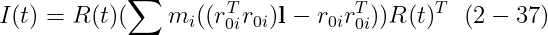
만약 우리 I_body를 이전의 행렬로 정의한다면
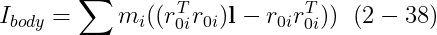
우리는 다음을 갖는다
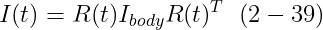
I_body가 body space에서 명시되기 때문에, 그것은 시뮬레이션 동안 상수이다. 따라서, 시뮬레이션이 시작되기 전에 I_body를 한 body에 대해 미리 연산하여, 우리는 쉽게 I_body와 orientation matrix R(t)로부터 I(t)를 연산할 수 있다. Section 5.1은 body space에서 body의 volume에 대해 적분의 관점에서 rectangular object에 대한 body-space inertia tensor를 유도한다.
또한 I(t)의 역행렬은 다음의 공식으로 주어진다
회전행렬에 대해, R(t)^T = R(t)^-1이고, R(t)^T^T는 R(t)이다. 명백히, I^-1_body는 또한 시뮬레이션 동안 상수이다.
2.11 Rigid Body Equations of Motion
마침내, 우리는 상태 벡터 X(t)를 정의하는데 필요한 모든 개념들을 다루었다! rigid body에 대해 우리는 X(t)를 다음으로 정의할 것이다
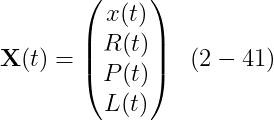
따라서, rigid body의 한그 상태는 그것의 위치와 방향 (spatial information을 묘사하는), 그리고 그것의 linear and angular momentum이다 (velocity information을 묘사하는). body의 질량 m과 body-space inertia tensor I_body는 상수이다, 그리고 우리는 시뮬레이션이 시작할 때 그것을 안다고 가정한다. 어떤 주어진 시간에 대해,
auxiliary quantities I(t), 𝞈(t), v(t)는 다음으로 연산된다
(2-42)
미분은 d/dx(X(t))
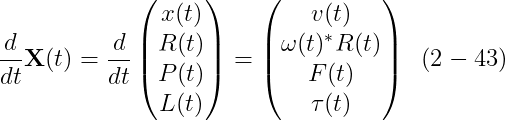
다음 섹션은 d/dt(X(t))를 연산하는 Dxdt() 함수에 대한 구현을 준다.
One final note: body의 orientation을 X(t)에서 행렬 R(t)로 표현하기 보다, quaternions를 사용하는 것이 더 좋다. Section 4는 회전 행렬의 자리에 쿼터니언을 사용하는 것을 다룬다. 간단히, 한 쿼터니언은 한 회전을 표현하기 위해 사용될 수 있는 4개의 요소를 가진 벡터의 한 타입이다. 만약 우리가 X(t)에 있는 R(t)를 쿼터이너 q(t)로 바꾼다면, 우리는 R(t)를 q(t)로부터 직접 연산되는 auxiliary variable로 다룰 수 있다, 𝞈(t)가 L(t)로부터 연산되듯이. Section 4는 \dot(R)(t) = 𝞈(t)^* R(t)와 유사한 공식을 도출한다, 그것은 q(t) and 𝞈(t)의 관점에서 dot(q)(to)를 표현하는 것이다.
3 Computing d/dx(X(t))
rigid bodies에 대한 Dxdt()함수의 구현을 고려해보자. 그 코드는 C++로 쓰여지고, 우리는 우리가 matrix와 triple이라고 불려진 데이터 타입 (클래스들)을 가진다고 가정할 것이다, 각각 3x3 행렬이고, 3-space에 있는 점이다. 이러한 데이터 타입을 사용하여 우리는 구조체르 rigid body를 나타낼 것이다
그리고 bodies의 global array를 가정한다
RigidBody bodies[NBODIES];
//... 생략 ... ///
4 Quaternions vs. Rotatoin Matrices
3x3 rotation matrix를 사용하는 것 보다 rigid body의 orientation을 나타내는데 더 좋은 방법이 있다. 많은 이유 때문에, 단위 길이로 표준화된 4개의 원소를 가진 벡터의 유형인 unit quaternions는 rotation matrices보다 더 좋은 선택이다.
Rigid Body simulation에 대해, 회전 행렬을 사용하는 것을 피하는 가장 중요한 이유는 numerical drift 때문이다. 우리가 다음의 공식으로 rigid body의 orientation을 추적한다고 가정하자.
dot(R)(t) = 𝞈(t)^* R(t).
우리가 이 공식을 사용하여 R(t)를 업데이트 할 때 (즉, 우리가 이 방정식을 적분할 때), 우리는 필연적으로 drift를 만날 것이다. Numerical error는 R(t)의 계수에서 축절될 것이고, 더 이상 R(t)가 정확히 회전행렬이 되지 않게 할 것이다. 그래픽적으로, 그 효과는 R(t)를 한 바디에 적용시키는 것이 skewing effect를 발생할 것이다.
이 문제는 rotations을 단위 쿼터니언으로 표현하여 경감될 수 있다. 쿼터니언들은 오직 4개의 파라미터만을 가지기 때문에, 회전의 세 개의 자유도를 표현하는데 사용되는 한 개의 추가 변수가 있다. 대조적으로 회전 행렬은 세 개의 자유도를 표현하기 위해 9개의 파라미터들을 상요한다; 그러므로, 중복의 정도는 눈에 띄개 회전행렬보다 쿼터니언에게 더 낮다. 결과적으로, 쿼터니언은 회전 행렬보다 drift를 덜 겪는다. 만약 그것이 쿼터니언에 있는 drift를 설명하는데 필수적이게 된다면, 쿼터니언은 그것의 단위 길이를 잃기 때문에 그럴 수 있다. 이것은 쉽게 쿼터니언을 단위 길이로 renormalizing하여 수정될 수 있따. 이러한 두 특성 때문에, 한 body의 orientation을 직접적으로 단위 쿼터니언 q(t)로 나타내는 것이 바람직하다. 우리는 여전히 angular velocity를 vector 𝞈(t)로 표현할 것이다. I^-1(t)를 연산하는데 필요한 orientation matrix R(t)는 q(t)로부터 auxiliary variable로 연산될 것이다.
/.. 생략 ../
한 단위 축 u에 대한 𝛉의 한 회전 단위 쿼터니언 다음으로 표현된다
회전을 나타내는데 쿼터니언을 사용해서, 만약 q_!과 q_2가 회전을 나타낸다면, 그러면 q_2 q_1은 q_1 다음에 q_2의 합성 회전을 나타낸다. 이제, 우리는 orientation을 위한 쿼터니언 표기를 위해 section 3의 routines을 어덯게 바꿀지를 보여줄 것이다. 우리가 이러한 변화를 하기전에, 우리는 dot(q)(t)에 대한 공식이 필요할 것이다. Appendix B는 그 공식을 유도한다
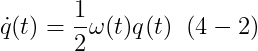
𝞈(t)q(t)의 곱은 쿼터니언 [0, 𝞈(t)과 q(t) 사이의 곱을 짧게 쓴 것이다. 방정식 (4-2)와
dot(R)(t) = 𝞈(t)^* R(t) 사이의 유사성에 주목해라.
// 생략 ... //
5 Examples
5.1 Inertia Tensor of a Block
그림 7에서 정사각형 블럭의 inertia tensor I_body를 계산해보자. 그 블럭은 x_0 X y_0 X z_0의 크기를 갖는다. 요구되듯이, 그 블럭의 center of mass는 원점에 있다. 따라서, 그 block의 크기는 x축을 따라서 -x0/2 부터 x0/2이고, y와 z축에 대해서 같다. inertia tensor를 계산하기 위해서, 우리는 방정식 (2-32)에 있는 그 합을 블럭의 부피에 대한 적분으로 다뤄야만 한다.
(2-32)
그 블럭은 상수의 단위 density를 가진다고 가정하자. 이것은 𝛒(x,y,z) density function이 항상 1이라는 것을 의미한다. 그 블럭은 x0y0z0의 부피를 갖기 떄문에, 그 블럭의 질량 M은 M = x0y0z0을 갖는다. 그러고나서, body space에서
유사하게, I_yy = M/12(x^2_0 + z^2_0이고, I_zz = M/12(x^2_0 + y^2_0)이다. 이제 대각선이 아닌 항에 대해 I_xy와 같은
I_xy = 0 (5-2)
적분은 모두 대칭이기 떄문이다. 따라서, 그 블럭의 inertia tensor는
5.2 A Uniform Force Field
한 body의 각 파티클에 uniform force가 작용한다고 가정하자. 예를들어, 우리는 일반적으로 중력장을 한 rigid body의 각 파티클에 m_ig의 force를 발휘하는 것으로 묘사한다. 거기에서 g는 아래쪽을 가리키는 벡터이다. 중력에 의해 body에 작용되는그 net force F_g는
F_g = sum m_i g= Mg (5-4)
이것은 center of Mass에 대해 Mg/g = g라는 가속도를 만들어 낸다. 중력장에 의한 torque는 무엇인가? 그 net torque는 방정식 (2-20)에 의해 0이다. 우리는 uniform gravitational field가 body의 angular momentum에 어떠한 효과도 가질 수 없다는 것을 알게 된다. 게다가, 중력장은 그것의 CM에 BODY에 작용하는 단일 힘 Mg로 다뤄질수 있다.
5.3 Rotation Free Movement of a Body
이제, 우리가 그림 8의 block에 작용하는 어떤 forces를 고려해보자. 한 외부 힘 F = (0, 0, f)가 점 x(t) + (-3, 0, 2)와 x(t) + (3, 0, -2)에 작용ㅇ한다고 가정하자. 우리는 이 것이 그 body가 angularly하게 가속되는 것 없이 linearly하게 가속되기를 기대할 것이다. 그 body에 작용한 net force는 (0, 0, 2f)이다. 그래서 CM의 가속도는 z축을 따라서 2f / M이다.
x(t) + (-3, 0, -2)에 작용한 그 force에 의한 torque는
~~
total torque 𝞽 = [0 0 -2] X F이다.
그러나 이것은 𝞽 = 0 을 준다.
기대되듯이, 그 블럭에 작용하는 힘들은 그 블럭에 어떠한 angular acceleration을 주지 않는다.
5.4 Translation Free Movement of a Body
외부 힘 F_1 = (0, 0, f)가 x(t) + (-3 , 0, -2)에 작용하고, 외부힘 F2가 (0, 0,-f)가 x(t) + (3, 0, 2)에 작용한다고 가정하자 (그림 9). F_1 = -F_2이기 때문에, 그 블럭에 작용하는 force는 F1 + F2 = 0이다. 그래서 CM에 어떠한 가속도가 없다. 반면에, net torque는
= [0 6f 0] 이다.
그리고 이것은 y축에 대해 평행이다. 최종 결과는 그 블럭에 작용하느 forces는 y축에 대해 angularly하게 가속을 일으킬 것이다.
5.5 Forces vs. Torque Puzzle
한 body에 있는 한 point에 작용하는 한 force의 효과를 고려할 때, 가끔식 force가 두 번 고려되는 것처럼 보인다. 즉, 만약 한 force F가 공간에서 r + x(t)의 한 점에 있는 body에 작용한다면, 그러면 우리는 처음에 F를 CM을 가속하는 것으로 고려하고, F를 body에 spin을 주는 것으로 고려한다.
이것은 처음에 역석처럼 보이는 것을 발생시킨다: 그림 10의 긴 수평 block을 고려하자, 그것은 초기에 쉬고있다. 한 force F가 어떤 시간 주기 동안 CM에 그 블럭에 작용된다고 가정하자. 가령 10초. 그 힘은 CM에 작용하기 때문에 어떠한 torque도 그 body에 발휘되지 않는다. 10초 후에, 그 body는 몇 가지 linear velocity v를 얻을 것이다. 그 body는 어떠한 angular velocity를 얻지 않을 것이다: 따라서 그 block의 kinetic energy는 1/2M|v|^2 이다.
이제 그 같은 force F가 그림 11에서 보여지듯이 body의 중심을 벗어나서 적용된다고 가정하자. 그 body에 적용되는 force는 같기 떄문에, CM의 가속도 같다. 따라서,10 초후에, 그 BODY는 다시 linear velocity v를 얻는다. 그러나, 10초 뒤에, 그 body는 center를 벗어나 작용하는 force F가 body에 torque를 발휘하기 떄문에 어떤 angular velocity 𝞈를 갖게 될 것이다. 그 kinetic energy는 (appendix C를 보아라) 1/2M|v|^2 + 1/2𝞈^TⅠ𝞈이다.
그 블럭의 kinetic energy는 CM을 통해 작용된 force 때 보다 더 높다. 그러나 만약 동일한 forces가 두 경우에 block을 밀었다면, 어떻게 그 block의 에너지가 다를 수 있는가?
Hint : Energy, or work, 는 거리에 따른 force의 적분이다.
그림 12는 center 바깥으로 작용한 force가 더 높은 kinetic energy를 발생시키는지에 대한 이유를 보여준다. 그 블럭의 kinetic energy는 force에 의해 처리된 work와 같다. force에 의해 처리된 work는 그 force를 적용하는데 이동된 거리에 대한 force의 적분이다. 그림 11에서, 그 force는 CM에 벗어나서 적용되는데, 그 force가 적용되는 점을 따라 추적되는 경로를 고려해라. 이 경로는 명백히 그림 10에서 CM에 의해 취해지는 경로보다 더 길다. 따라서, 그 FORCE가 center에 벗어나서 적용될 때, 좀 더 많은 work가 처리된다. 왜냐하면 force가 적용되는 점 p가 CM에 적용될 때 보다 더 많은 경로를 그린다.
Introduction
이 과목의 이 부분은 Rigid Body Dynamics의 문제를 다룬다. Rigid Body Motion을 재현하는 것을 시작하는 것을 돕기 위해, 우리는 이러한 notes들에서 이야기되는 대부분의 개념들을 구현하는 code fragments를 제공한다. 그 course notes의 이 segment는 두 개의 부분으로 나눠진다. 그 첫 번째 파트는 그것들의 허용될 수 있는 움직임에서 완전히 unconstrained(제약 받지 않는) rigid bodies의 움직임을다룬다; 즉, rigid bodies 사이의 충돌에 대한 관련이 없는 simulation이다. 어떤 외부의 forces가 주어진다면, 우리는 이러한 forces에 대응하여 그 body의 움직임을 어떻게 재현할지를 보여줄 것이다. 이러한 notes에서 수학적 유도는 꽤 공식적이고(informal) 직관적이 되도록 의도된다.
그 notes의 두 번째 부분은 우리가 bodies를 solid라고 간주할 때, 그리고 inter-penetration을 허용하지 않을 필요가 있을 때 발생하는 constrained motion의 문제를 다룬다. 우리는 접촉하는 bodies 사이의 적절한 contact forces를 연산하여, 이러한 non-penetration constraints (관통하는 것이 없는 제약) 를 실행한다. 이러한 contact forces에 대한 값이 주어진다면, unconstrained case에서 처럼 정확히 시뮬레이션이 진행된다 : 우리는 모든 forces를 그 bodies에 적용하고, 그 시뮬레이션이 bodies의 움직임에 완전히 제약받지 않는 것처럼 진행되도록 한다. 만약 우리가 contact forces를 정확히 연산헀다면, 그 bodies의 최종 움직임은 inter-penetration으로부터 자유로울 것이다. 이러한 contact forces의 계산은 전체 시뮬레이션 프로세스에서 가장 까다로운 component이다.
Part 1. Unconstrained Rigid Body Dynamics
1 Simulation Basics
course notes의 이 부분은 rigid body motion의 완전한 구현을 위해서 맞춰진다. 이 섹션에서, 우리는 한 rigid body의 움직임을 재현하는 기본 구조를 보여줄 것이다. section 2에서, 우리는 rigid body simulator를 구현하는데 필요한 용어, 개념, 방정식들을 정의할 것이다. 이것을 따라서, 우리는 우리가 필요한 방정식을 실제로 구현하는 몇 가지 코드를 줄 것이다. 우리가 사용할 그 개념과 방정식에 대한 유도는 appendix A에 남겨질 것이다.
이 지점에서 너가 친숙해질 필요가 있는 유일한 것은 Ordinary Differential Equations를 해결하는 것의 기본 개념이다 (numerical details가 아닌). 만약 너가 이 주제에 익숙하지 않다면, 너는 운이 좋다 : 이 course notes의 처음에로 돌아가서, "Differential Equation Basics" 섹션을 읽어라. 너는 또한 "Particle Dynamics"의 다음 섹션을 읽길 원할지도 모른다. 비록 우리가 여기에서 그 자료의 몇 가지를 반복하려고 할지라도.
rigid body의 움직임을 재현하는 것은 거의 파티클의 움직임을 재현하는 것과 같다. 그래서 파티클 시뮬레이션으로 시작하자. .... 생략 ...
2 Rigid Body Concepts
이 섹션의 목표는 rigid bodies에 대해 방정식 (1-3)과 유사한 것을 개발하는 거싱다. 우리가 개발할 최종 미분방정식은 section 2.11에서 주어진다. 이것을 하기 위해서, 우리는 처음에 많은 개념들을 정의하고 관계들을 정의할 필요가 있다. 더 긴 유도들 몇 가지는 appendix A에 있다. 다음 섹션에서, 우리는 이 섹션에서 개발된 X(t)의 미분을 연산하기위해 numerical solver ode에 필요한 함수 Dxdt()를 어떻게 작성하는지를 보여줄 것이다.
2.1 Position and Orientation
.... rigid body를 world space에서 위치시키기 위해, 우리는 x(t)라는 벡터를 사용할 것인데, 이것은 그 body의 평행이동을 묘사한다. 우리는 또한 그 body의 회전을 묘사해야만 하는데, 우리는 그것을 3x3 rotation matrix R(t)의 관점에서 할 것이다. 우리는 x(t)와 R(t)를 한 rigid body의 spatial variables라고 부를 것이다.
파티클과 다르게, 한 rigid body는 공간의 한 부피를 차지하고, 특별한 모양을 갖는다. 한 rigid body는 오직 회전과 평행이동만을 겪을 수 있기 때문에, 우리는 body space라고 불려지는 고정되고 불변하는 공간에서의 관점에서 rigid body의 모양을 정의할 수 있다. body space에서 body의 기하학적 묘사가 주어진다면, 우리는 body-space description을 world space로 transform하기위해 x(t)와 R(t)를 사용한다. 우리가 사용할 몇 가지 방정식을 간단하게 하기 위해, 우리는 body space에서 rigidbody의 우리의 묘사가 body의 center of mass가 원점 (0,0,0)에 있도록 요구한다. 우리는 CM을 좀 더 정확히 나중에 정의할 것이지만, CM은 그 body의 기하학적 중심에 놓여있는 rigid body의 한 점으로 생각되어질 수 있다. body의 shape를 묘사할 때, 우리는 이 geometric center가 body space에서 (0,0,0)에 있도록 요구한다. 만약 우리가 R(t)가 center of mass에 대한 body의 회전을 명시하는 것을 동의한다면, body space에 있는 한 고정된 벡터 r은 time t에 R(t) * r의 world space 벡터로 회전될 것이다. 마찬 가지로, p_0은 body space에서 rigid body의 임의의 점이라고 한다면, 그러면 p_0의 world-space location p(t)는 원점에 대해 p_0을 먼저회전 시키고나서, 그것을 평행이동 시킨 결과가 될 것이다
p(t) = R(t)p_0 + x(t). (2-1)
body의 CM이 원점에 놓여있기 때문에, CM의 world-space location은 항상 x(t)에 의해서 직접적으로 주어진다. 이것은 x(t)가 time t에 world space에 있는 CM의 위치라는 것을 말하여서 x(t)에 대한 물리적인 의미를 붙이도록 해준다. 우리는 또한 R(t)에 물리적인 의미를 붙일 수 있다. 즉, body space에서 x축이 vector (1, 0, 0)이라고 고려하자. time t에서, 이 벡터는 world space에서 다음의 방향을 갖는다.
만약 우리가 R(t)의 컴포넌트들을 다음과 같이 쓴다면
그러면
가 되고, 이것은 R(t)의 첫 번째 열이다. R(t)의 물리적인 의미는, time t에 world space로 변환될 때 R(t)의 첫 번째 열은 rigid body의 x축이 가리키는 방향을 준다는 것이다. 유사하게, R(t)의 두 번째와 세번째 열들도 time t에 world space에서 rigid body의 y와 z축들의 방향을 준다.
2.2 Linear Velocity
간단함을 위해서, 우리는 x(t)와 R(t)를 time t에서 body의 position과 orientation이라고 부를것이다. 다음으로 우리가 할 필요가 있는 것은 시간에 대해 position과 orientation이 어떻게 변하는지를 정의하는 것이다. 이것은 우리가 dot(x)(t)와 dot(R)(t)에 대한 표현이 필요하다는 것을 의미한다. x(t)가 world space에서 CM의 위치이기 때문에, dot(x)(t)는 world space의 CM의 velocity가 된다. 우리는 linear velocity v(t)를 이 속도로 정의할 것이다:
v(t) = dot(x)(t) (2-4)
만약 우리가 body의 orientation이 고정되어있다고 상상한다면, 그러면 그 body가 격을 쑤 있는 유일한 움직임은 순수한 평행이동이다. 그 v(t) 양은 이 translation의 속도를 준다.
2.3 Angular Velocity
평행이동 하는 것 외에도, rigid body는 또한 회전할 수 있다. 우리가 CM의 위치가 공간에서 움직일 수 없게 했다고 상상해라. 그 몸의 점들의 어떤 움직임은 그러므로 그 body에 의해 CM을 지나는 어떤 축에 대해 회전해야만 한다. (그렇지 않다면 그 CM자체만 회전할 것이다). 우리는 그 spin을 한 벡터 𝞈(t) 로 묘사할 수 있다. 𝞈(t)의 방향은 그 body가 회전하고 있는 축의 방향을 준다 (그림 3). 𝞈(t)의 크기, |𝞈(t)|는 그 body가 얼마나 빠르게 회전하고 있는지를 말한다. |𝞈(t)|는 revolutions/time의 관점을 가지고 있다; 따라서 |𝞈(t)|는 그 body가 주어진 시간 동안 회전할 angle과 연관짓는다, 만약 그 angular velocity가 변하지 않는다면. 그 quantity 𝞈(t)는 angular velocity라고 불려진다.
linear velocity에 대해, x(t)와 v(t)는 v(t) = d/dt x(t)와 연관된다. R(t)와 𝞈(t)는 어떻게 연관되는 가? (명백히, dot(R)(t)는 w(t)가 될 수 없다, 왜냐하면 R(t)가 행렬이고 w(t)는 벡터이기 때문이다.) 이 질문에 답하기 위해서, 우리는 R(t)의 물리적인 의미를 상기하도록 하자. 우리는R(t)의 columns들이 우리에게 time t에서 변환된 x, y and z body axes의 방향을 말해준 다는 것을 안다. w(t)와 R(t) 사이의 관계를 발견하기 위해, rigid body에서 임의의 벡터가 angular velocity 𝞈(t)와 어떻게 연관되는지를 시험해보자.
그림 4는 angular velocity 𝞈(t)를 가진 rigid body를 보여준다. world space에서 명시된 time t 에서의 한 벡터 r(t)를 고려해라. 우리가 이 벡터가 그 body에 고정되어 있다고 고려한다고 가정하자; 즉, r(t)는 world space를 통해 그 rigid body와 함께 움직인다. r(t)는 한 방향이기 때문에, 그것은 어떤 평행이동 효과와 무관하다; 특히, dot(r)(t)는 v(t)와 독립적이다. dot(r)(t)를 공부하기 위해서, 우리는 r(t)를 벡터 a와 b로 분해하는데, a는 w(t)와 평행하고, b는 w(t)와 수직이다. rigid body가 constant angular velocity를유지한다는 것을 가정하자, r(t) 벡터의 끝이 instantaneously하게 이 원을 따라 움직이기 때문에, r(t)의 instantaneous change는 b와 w(t) 둘 다에 수직이다. r(t)의 tip이 반지름이 b인 한 원에서 움직이고 있기 때문에, r(t)의 instantaneous velocity는 |b||w(t)|의 크기를 갖는다.
b와 w(t)가 수직이기 때문에 그것들의 외적은 그 크기를 갖는다
이 것을 합하여, 우리는 dot(r)(t) = w(t) X (b) 라고 쓸 수 있다. 그러나, r(t) = a + b이고, a는 w(t)에 평행하기 때문에, 우리는 w(t) X a = 0을 갖는다 따라서
따라서, 우리는 간단히 한 벡터의 변화율을 간단히 다음으로 표현할 수 있다
이것은 이제 모두 합쳐보자. time t에서, 우리는 world space에서 rigid body의 x 축의 방향이 [ r_xx r_xy r_xz ] 인 것을 알고,
time t에서 R(t)의 첫 번째 column의 미분이 이 벡터의 변화율이라는 것을안다: 우리가 발견한 외적 법칙을 사용하여 이 변화는
그 같은 것이 명백히 R(t)의 다른 두 개의 열들에도 유효하다. 이것은 우리가 다음을 쓸 수 있게 한다.
이것은 가지고 다니기에 너무 번거로운 수식이다. 간단하게 하기 위해서, 우리는 다음의 trick을 사용한다. 만약 a와 b가 3-vectors라면, 그러면 a x b는 다음의 벡터가 되고,
vector a가 주어진다면 a* 를 다음의 행렬이 되도록하자 (skew-symmetric matrix)
그러고나서,
a*b = a x b (2-9)
가 된다.
* notation을 사용하여, 우리는 dot(R)(t)를 좀 더 간단히 쓸 수 있다.
결국에 우리는 다음을 얻는다
마지막으로, 이것은 우리에게 dot(R)(t)와 w(t) 사이에 원했던 관계를 준다.
한 벡터에 대해 dot(r)(t) = w(t) X r(t) 와 rotation matrix에 대해 dot(R)(t) = w(t)* R(t) 사이의 대응에 주목해라.
2.4 Mass of a Body
몇 가지 유도를 처리하기 위해서, 우리는 (개념적으로) 우리의 rigid body의 부피에 대해 어떤 적분을 수행할 필요가 있을 것이다. 이러한 유도를 더욱 간단하게 하기 위해, 우리는 일시적으로 한 rigid body가 수 많은 작은 파티클들로 구성되었다고 상상할 것이다. 그 파티클들은 1에서 N까지 인덱싱된다. i번째 파티클의 질량은 m_i이고, 각 파티클은 body space에서 r_0i의 (constant) 위치를 갖는다. time t에서 world space에 있는 i번째 파티클의 위치는 r_i(t)로 표기되고, 그러므로 다음의 공식에 의해 주어진다
그 body의 total mass, M은 다음의 합계이다
(이후로, 합계는 인덱스 변수 i로 1부터 N까지 합으로 가정된다.)
2.5 Velocity of a Particle
i번째 파티클의 velocity dot(r)_i(t)는 2-13 방정식을 미분하여 얻어진다: dot(R)(t) = w* R(t)의 관계를 사용하여 우리는 다음을 얻는다
우리는 이것을 다음으로 쓸 수 있다
방정식 2-13으로부터 r_i(t)의 정의를 사용해서. "*" operator의 정의로부터,
어떤 벡터 a에 대해 w(t) * a = w(t) X a라는 것을 회상해라. 이것을 사용하여, 우리는 간단히 쓸 수 있다
이것은 rigid body의 한 점의 velocity를 두 개의 컴포넌트로 분리한다 (그림 5) : linear component v(t)와 angular component w X (r_i(t) - x(t))
2.6 Center of Mass
CM의 우리의 정의는 마찬가지로 bodies의 dynamics를 linear and angular components로 분해할 수 있게 할 것이다. world space에서의 한 body의 CM은 다음으로 정의된다
여기에서 M은 그 body의 mass이다 (즉, 개별 질량 m_i의 합). 우리가 CM 좌표계를 사용한다고 말할 때, 우리는 BODY SPACE에서
를 의미하게 된다. (즉, CM이 원점이여야 한다는 것이다)
이것이 Sum(m_ir_0i) = 0 이라는 것을 또한 암시한다는 것에 주의해라.
우리는 x(t)가 time t에서 CM의 위치라고 말했었다. 이것은 사실인가? 그렇다: i번째 파티클은 time t에 position r_i(t) = R(t)r_0i + x(t)를 가지기 때문에, time t에서의 CM은
부가적으로
의 관계를 아는 것은 또한 중요하다.
2.7 Force and Torque
우리가 어떤 외부 영향 (예를들어, 중력, 바람, contact forces)에 의해 rigid body에 작용하는 한 force를 상상할 때, 우리는 그 force가 그 body의 한 특정한 particle에 작용한다고 상상할 수 있다. (우리의 파티클 모델을 개념적으로만 생각해라. 우리는 어떤 기하학적 위치에 한 force를 작용시킬 수 있고 또는 body안에 작용시킬 수 있다, 왜냐하면 우리는 항상 그 정확한 위치에서의 한 파티클이 있다고 상상할 수 있기 때문이다.) 그 force가 작용하는 particle의 위치는 그 force가 작용하는 위치를 정의한다. 우리는 F_i(t)가 time t에서 i번째 파티클에 작용하는 외부 forces로부터 온 total force라고 표기한다. 또한, 우리는 𝛕_i(t)를 i번째 파티클에 작용하는 external torque로 다음과 같이 정의한다
한 파티클에서 Torque CM x(t)를 기준으로한 그 파티클의 r_i(t)의 위치에 의존한다는 점에서 force와 Torque는 다르다. 우리는 직관적으로 𝛕_i(t)의 방향을 body가 F_i(t)에 의해 회전하는 축이 된다고 생각할 수 있다, 만약 CM이 완전히 제자리에 있다면 (그림 6).
그 body에 작용하는 total external force F(t)는 F_i(t)의 합계이다:
반면에 total torque는 유사하게 정의도니다
F(t)가 다양한 forces가 그 body에 어디에서 작용되었는지에 대한 정보를 전달하지 않는 것을 주목해라; 그러나 𝛕_(t)는 우리에게 body에 대한 forces F_i(t)의 distribution에 대한 어떤 것을 말해준다.
2.8 Linear Momentum
질량 m과 속도 v를 갖는 한 파티클의 linear momentum p는 다음으로 정의된다
한 rigid body의 total linear momentum P(t) 는 각 파티클의 mass and velocity의 곱의 합이다:
방정식 (2-17)로부터, i번째 파티클의 velocity dot(r)_i는
이고,
따라서, 그 body의 total linear momentum은
우리는 CM 좌표계를 사용하고 있기 때문에, 우리는 (2-20)방정식을 적용할 수 있고 다음을 얻을 수 있다
이것은 우리에게 우리의 rigid body의 total linear momentum이 그 body가 마치 질량 M과 속도 v(t)를 가진 하나의 파티클 처럼 같게 하는 좋은 결과를 준다. 이것 때문에, 우리는 P(t)와 v(t)사이의 간단한 변환을 갖는다: P(t) = Mv(t)와 v(t) = P(t) / M. M이 상수이기 때문에
linear momentum의 개념은 우리가 꽤 간단하게 한 rigid body의 total force F(t)의 효과를 표현하게 해준다. Appendix A는 다음의 관계를 유도한다
그리고 이것은 linear momentum의 변화가 한 body에 작용하는 total force와 같은 것이라고 말한다. P(t)가 우리에게 한 body의 rotational velocity에 대해서 어떠한 것도 말하지 않는다는 것에 주목해라. 이것은 좋은 것이다. 왜냐하면 F(t)는 또한 한 body의 rotational velocity의 변화에 대해서도 어떠한 것도 전달하지 않기 때문이다!
P(t)와 v(t) 사이의 관계가 간단하기 때문에, 우리는 P(t)를 우리의 rigid body의 상태 변수로 사용할 것이다, v(t) 대신에. 우리는 v(t)가 물론 상태 변수가 되게 할 수 있고, 다음의 관계를 사용하게 할 수 있다.
그러나, v(t) 대신에 P(t)를 상태 변수로 사용하는 것은 우리가 angular velocity와 acceleration을 다루는 방식과 좀 더 일관될 것이다.
2.9 Angular Momentum
linear momentum의 개념이 꽤 직관적인 반면에 (P(t) = Mv(t)), (rigid body에 대한) angular momentum의 개념은 그렇지 않다. 어떤 사람이 한 rigid body의 angular momentum에 시달리는 유일한 이유는, 만약 너가 angular velocity를 고수한다면 그것이 너가 얻는 것 보다 더욱 간단한 방정식을 쓰게 할 것이기 때문이다 - 그것은 가장 직관적이지 않은 개념이다. Angular momentum은 방정식을 결국에 간단하게 할 것이다. 왜냐하면 그것은 자연에서 그렇게 보존되기 때문이다, 반면에 angular velocity는 그렇지 않다: 만약 너가 body에 어떠한 torque도 작용하지 않는 공간을 통해 떠다니는 한 body를 갖는다면, 그 body의 angular momentum은 상수이다. 이것은 그런데 body의 angular velocity에 사실이 아니다: 비록 한 body의 angular momentum이 상수일지라도, 그 body의 angular velocity는 그렇지 않을 것이다! 결과적으로 한 body의 angular velocity는 어떠한 force가 body에 작용하지 않을 때에 변할 수 있다. 이것 때문에, angular momentum을 angular velocity보다 상태변수로 선택하는게 더 간단하게 된다.
linear momentum에 대해, 우리는 P(t) = Mv(t)의 관계를 갖는다. 유사하게, 우리는 rigid body의 total angular momentum L(t)를 다음의 방정식으로 정의한다 L(t) = I(t)w(t), 여기에서 I(t)는 inertia tensor이라고 불리는 우리가 곧 설명할 3x3 행렬이다 (기술적으로 rank-two tensor). 그 inertia tensor I(t)는 body에 있는 그 질량이 그 body의 CM을 기준으로 어떻게 분배되었는지를 묘사한다. 그 tensor I(t)는 한 body의 방향에 의존하지만, body의 평행이동에 의존하지 않는다. angular and linear case 둘 다에 대해, momentum은 velocity의 linear function 이라는 것을 주목해라 - angular case에서 scaling factor이고, 반면에 linear case에서 그것은 단순히 scalar이다. L(t)가 어떤 평행이동 효과와 독립적이라는 것에 주목해라, 반면에 P(t)는 어떠한 회전 효과와 독립이다.
L(t)와 𝞽(t)사이의 관계는 매우 간단하다: Appendix A는 다음을 유도한다
이것은 dot(P)(t) = F(t) 와의 관계와 유사하다.
2.10 The Inertia Tensor
그 inertia tensor I(t)는 angular momentum L(t)와 angular velocity 𝞈(t) 사이의 scaling factor이다. 주어진 시간 t에서, r'_i가 r'_i = r_i(t) - x(t)로 정의하여 x(t)로부터 i번째 파티클의 변위라고 하자. 그 tensor I(t)는 r'_i의 관점으로 대칭 행렬로 표현된다
실제 구현에 대해, 우리는 world space에서 한 body의 부피에 대해 적분으로 유한의 합을 대체한다. 그 질량 항 m_i는 density function으로 대체된다. 처음에 볼 떄, 우리는 방향 R(t)가 바뀔 때 마다 I(t)를 찾기 위해 이러한 적분을 할 필요가 있는 것처럼 보인다. 이것은 시뮬레이션동안 엄두를 못낼 만큼 하기에 비싸다. 만약 그 body의 shape가 너무 간단하지 않아서 그 적분이 symbolicaly하게 얻어질 수 있지 않다면.
운 좋게도, body-space coordinates를 사용하여, 우리는 body-space coordinates에서 미리 연산된 적분의 관점에서 값 싸게 어떤 방향 R(t)에 대한 inertia tensor를 연산할 수 있다. (이 적분은 일반적으로 시뮬레이션이 시작되기 전에 연산되고, body의 물리적 특성을 묘사하는 그 입력 파라미터들 중 하나로 간주되어질 것이다.) r'^T_i r'_i = r'^2_ix + r'^2_iy + r'^2_iz라는 사실을 사용하여, 우리는 I(t)를 뺄셈으로 다시 쓸 수 있다
r'_i 자기 자신괴 외적곱을 취하여, 즉
l은 3x3 identity matrix를 나타내게 하여, 우리는 I(t)를 간단히 다음으로 표기한다
이것이 어떻게 도움이 되는가?
r_i(t) = R(t)r_0i + x(t) 이기에, r_0i는 상수이고, r'_i = R(t)r_0i 이다. 그러므로, R(t)R(t)^T = l이기 떄문에
r^T_0i r_0i는 scalar이기 때문에, 우리는 다시 쓸 수 있다
만약 우리 I_body를 이전의 행렬로 정의한다면
우리는 다음을 갖는다
I_body가 body space에서 명시되기 때문에, 그것은 시뮬레이션 동안 상수이다. 따라서, 시뮬레이션이 시작되기 전에 I_body를 한 body에 대해 미리 연산하여, 우리는 쉽게 I_body와 orientation matrix R(t)로부터 I(t)를 연산할 수 있다. Section 5.1은 body space에서 body의 volume에 대해 적분의 관점에서 rectangular object에 대한 body-space inertia tensor를 유도한다.
또한 I(t)의 역행렬은 다음의 공식으로 주어진다
회전행렬에 대해, R(t)^T = R(t)^-1이고, R(t)^T^T는 R(t)이다. 명백히, I^-1_body는 또한 시뮬레이션 동안 상수이다.
2.11 Rigid Body Equations of Motion
마침내, 우리는 상태 벡터 X(t)를 정의하는데 필요한 모든 개념들을 다루었다! rigid body에 대해 우리는 X(t)를 다음으로 정의할 것이다
따라서, rigid body의 한그 상태는 그것의 위치와 방향 (spatial information을 묘사하는), 그리고 그것의 linear and angular momentum이다 (velocity information을 묘사하는). body의 질량 m과 body-space inertia tensor I_body는 상수이다, 그리고 우리는 시뮬레이션이 시작할 때 그것을 안다고 가정한다. 어떤 주어진 시간에 대해,
auxiliary quantities I(t), 𝞈(t), v(t)는 다음으로 연산된다
미분은 d/dx(X(t))
다음 섹션은 d/dt(X(t))를 연산하는 Dxdt() 함수에 대한 구현을 준다.
One final note: body의 orientation을 X(t)에서 행렬 R(t)로 표현하기 보다, quaternions를 사용하는 것이 더 좋다. Section 4는 회전 행렬의 자리에 쿼터니언을 사용하는 것을 다룬다. 간단히, 한 쿼터니언은 한 회전을 표현하기 위해 사용될 수 있는 4개의 요소를 가진 벡터의 한 타입이다. 만약 우리가 X(t)에 있는 R(t)를 쿼터이너 q(t)로 바꾼다면, 우리는 R(t)를 q(t)로부터 직접 연산되는 auxiliary variable로 다룰 수 있다, 𝞈(t)가 L(t)로부터 연산되듯이. Section 4는 \dot(R)(t) = 𝞈(t)^* R(t)와 유사한 공식을 도출한다, 그것은 q(t) and 𝞈(t)의 관점에서 dot(q)(to)를 표현하는 것이다.
3 Computing d/dx(X(t))
rigid bodies에 대한 Dxdt()함수의 구현을 고려해보자. 그 코드는 C++로 쓰여지고, 우리는 우리가 matrix와 triple이라고 불려진 데이터 타입 (클래스들)을 가진다고 가정할 것이다, 각각 3x3 행렬이고, 3-space에 있는 점이다. 이러한 데이터 타입을 사용하여 우리는 구조체르 rigid body를 나타낼 것이다
struct RigidBody { /* Constant Quantities */ double mass; /* mass M */ matrix Ibody, /* Ibody */ Ibodyinv; /* I^-1_body (inverse of I_body) */ /* State variables */ triple x; /* x(t) */ matrix R; /* R(t) */ triple P, /* P(t) */ L, /* L(t) */ /* Derived quantities (auxiliary variables) */ matrix Iinv; /* I^-1(t) */ triple v, /* v(t) */ omega; /* w(t) */ /* Computed quantities */ triple force, /* F(t) */ torque; /* t(t) */ };
그리고 bodies의 global array를 가정한다
RigidBody bodies[NBODIES];
//... 생략 ... ///
4 Quaternions vs. Rotatoin Matrices
3x3 rotation matrix를 사용하는 것 보다 rigid body의 orientation을 나타내는데 더 좋은 방법이 있다. 많은 이유 때문에, 단위 길이로 표준화된 4개의 원소를 가진 벡터의 유형인 unit quaternions는 rotation matrices보다 더 좋은 선택이다.
Rigid Body simulation에 대해, 회전 행렬을 사용하는 것을 피하는 가장 중요한 이유는 numerical drift 때문이다. 우리가 다음의 공식으로 rigid body의 orientation을 추적한다고 가정하자.
dot(R)(t) = 𝞈(t)^* R(t).
우리가 이 공식을 사용하여 R(t)를 업데이트 할 때 (즉, 우리가 이 방정식을 적분할 때), 우리는 필연적으로 drift를 만날 것이다. Numerical error는 R(t)의 계수에서 축절될 것이고, 더 이상 R(t)가 정확히 회전행렬이 되지 않게 할 것이다. 그래픽적으로, 그 효과는 R(t)를 한 바디에 적용시키는 것이 skewing effect를 발생할 것이다.
이 문제는 rotations을 단위 쿼터니언으로 표현하여 경감될 수 있다. 쿼터니언들은 오직 4개의 파라미터만을 가지기 때문에, 회전의 세 개의 자유도를 표현하는데 사용되는 한 개의 추가 변수가 있다. 대조적으로 회전 행렬은 세 개의 자유도를 표현하기 위해 9개의 파라미터들을 상요한다; 그러므로, 중복의 정도는 눈에 띄개 회전행렬보다 쿼터니언에게 더 낮다. 결과적으로, 쿼터니언은 회전 행렬보다 drift를 덜 겪는다. 만약 그것이 쿼터니언에 있는 drift를 설명하는데 필수적이게 된다면, 쿼터니언은 그것의 단위 길이를 잃기 때문에 그럴 수 있다. 이것은 쉽게 쿼터니언을 단위 길이로 renormalizing하여 수정될 수 있따. 이러한 두 특성 때문에, 한 body의 orientation을 직접적으로 단위 쿼터니언 q(t)로 나타내는 것이 바람직하다. 우리는 여전히 angular velocity를 vector 𝞈(t)로 표현할 것이다. I^-1(t)를 연산하는데 필요한 orientation matrix R(t)는 q(t)로부터 auxiliary variable로 연산될 것이다.
/.. 생략 ../
한 단위 축 u에 대한 𝛉의 한 회전 단위 쿼터니언 다음으로 표현된다
회전을 나타내는데 쿼터니언을 사용해서, 만약 q_!과 q_2가 회전을 나타낸다면, 그러면 q_2 q_1은 q_1 다음에 q_2의 합성 회전을 나타낸다. 이제, 우리는 orientation을 위한 쿼터니언 표기를 위해 section 3의 routines을 어덯게 바꿀지를 보여줄 것이다. 우리가 이러한 변화를 하기전에, 우리는 dot(q)(t)에 대한 공식이 필요할 것이다. Appendix B는 그 공식을 유도한다
𝞈(t)q(t)의 곱은 쿼터니언 [0, 𝞈(t)과 q(t) 사이의 곱을 짧게 쓴 것이다. 방정식 (4-2)와
dot(R)(t) = 𝞈(t)^* R(t) 사이의 유사성에 주목해라.
// 생략 ... //
5 Examples
5.1 Inertia Tensor of a Block
그림 7에서 정사각형 블럭의 inertia tensor I_body를 계산해보자. 그 블럭은 x_0 X y_0 X z_0의 크기를 갖는다. 요구되듯이, 그 블럭의 center of mass는 원점에 있다. 따라서, 그 block의 크기는 x축을 따라서 -x0/2 부터 x0/2이고, y와 z축에 대해서 같다. inertia tensor를 계산하기 위해서, 우리는 방정식 (2-32)에 있는 그 합을 블럭의 부피에 대한 적분으로 다뤄야만 한다.
그 블럭은 상수의 단위 density를 가진다고 가정하자. 이것은 𝛒(x,y,z) density function이 항상 1이라는 것을 의미한다. 그 블럭은 x0y0z0의 부피를 갖기 떄문에, 그 블럭의 질량 M은 M = x0y0z0을 갖는다. 그러고나서, body space에서
유사하게, I_yy = M/12(x^2_0 + z^2_0이고, I_zz = M/12(x^2_0 + y^2_0)이다. 이제 대각선이 아닌 항에 대해 I_xy와 같은
I_xy = 0 (5-2)
적분은 모두 대칭이기 떄문이다. 따라서, 그 블럭의 inertia tensor는
5.2 A Uniform Force Field
한 body의 각 파티클에 uniform force가 작용한다고 가정하자. 예를들어, 우리는 일반적으로 중력장을 한 rigid body의 각 파티클에 m_ig의 force를 발휘하는 것으로 묘사한다. 거기에서 g는 아래쪽을 가리키는 벡터이다. 중력에 의해 body에 작용되는그 net force F_g는
F_g = sum m_i g= Mg (5-4)
이것은 center of Mass에 대해 Mg/g = g라는 가속도를 만들어 낸다. 중력장에 의한 torque는 무엇인가? 그 net torque는 방정식 (2-20)에 의해 0이다. 우리는 uniform gravitational field가 body의 angular momentum에 어떠한 효과도 가질 수 없다는 것을 알게 된다. 게다가, 중력장은 그것의 CM에 BODY에 작용하는 단일 힘 Mg로 다뤄질수 있다.
5.3 Rotation Free Movement of a Body
이제, 우리가 그림 8의 block에 작용하는 어떤 forces를 고려해보자. 한 외부 힘 F = (0, 0, f)가 점 x(t) + (-3, 0, 2)와 x(t) + (3, 0, -2)에 작용ㅇ한다고 가정하자. 우리는 이 것이 그 body가 angularly하게 가속되는 것 없이 linearly하게 가속되기를 기대할 것이다. 그 body에 작용한 net force는 (0, 0, 2f)이다. 그래서 CM의 가속도는 z축을 따라서 2f / M이다.
x(t) + (-3, 0, -2)에 작용한 그 force에 의한 torque는
~~
total torque 𝞽 = [0 0 -2] X F이다.
그러나 이것은 𝞽 = 0 을 준다.
기대되듯이, 그 블럭에 작용하는 힘들은 그 블럭에 어떠한 angular acceleration을 주지 않는다.
5.4 Translation Free Movement of a Body
외부 힘 F_1 = (0, 0, f)가 x(t) + (-3 , 0, -2)에 작용하고, 외부힘 F2가 (0, 0,-f)가 x(t) + (3, 0, 2)에 작용한다고 가정하자 (그림 9). F_1 = -F_2이기 때문에, 그 블럭에 작용하는 force는 F1 + F2 = 0이다. 그래서 CM에 어떠한 가속도가 없다. 반면에, net torque는
= [0 6f 0] 이다.
그리고 이것은 y축에 대해 평행이다. 최종 결과는 그 블럭에 작용하느 forces는 y축에 대해 angularly하게 가속을 일으킬 것이다.
5.5 Forces vs. Torque Puzzle
한 body에 있는 한 point에 작용하는 한 force의 효과를 고려할 때, 가끔식 force가 두 번 고려되는 것처럼 보인다. 즉, 만약 한 force F가 공간에서 r + x(t)의 한 점에 있는 body에 작용한다면, 그러면 우리는 처음에 F를 CM을 가속하는 것으로 고려하고, F를 body에 spin을 주는 것으로 고려한다.
이것은 처음에 역석처럼 보이는 것을 발생시킨다: 그림 10의 긴 수평 block을 고려하자, 그것은 초기에 쉬고있다. 한 force F가 어떤 시간 주기 동안 CM에 그 블럭에 작용된다고 가정하자. 가령 10초. 그 힘은 CM에 작용하기 때문에 어떠한 torque도 그 body에 발휘되지 않는다. 10초 후에, 그 body는 몇 가지 linear velocity v를 얻을 것이다. 그 body는 어떠한 angular velocity를 얻지 않을 것이다: 따라서 그 block의 kinetic energy는 1/2M|v|^2 이다.
이제 그 같은 force F가 그림 11에서 보여지듯이 body의 중심을 벗어나서 적용된다고 가정하자. 그 body에 적용되는 force는 같기 떄문에, CM의 가속도 같다. 따라서,10 초후에, 그 BODY는 다시 linear velocity v를 얻는다. 그러나, 10초 뒤에, 그 body는 center를 벗어나 작용하는 force F가 body에 torque를 발휘하기 떄문에 어떤 angular velocity 𝞈를 갖게 될 것이다. 그 kinetic energy는 (appendix C를 보아라) 1/2M|v|^2 + 1/2𝞈^TⅠ𝞈이다.
그 블럭의 kinetic energy는 CM을 통해 작용된 force 때 보다 더 높다. 그러나 만약 동일한 forces가 두 경우에 block을 밀었다면, 어떻게 그 block의 에너지가 다를 수 있는가?
Hint : Energy, or work, 는 거리에 따른 force의 적분이다.
그림 12는 center 바깥으로 작용한 force가 더 높은 kinetic energy를 발생시키는지에 대한 이유를 보여준다. 그 블럭의 kinetic energy는 force에 의해 처리된 work와 같다. force에 의해 처리된 work는 그 force를 적용하는데 이동된 거리에 대한 force의 적분이다. 그림 11에서, 그 force는 CM에 벗어나서 적용되는데, 그 force가 적용되는 점을 따라 추적되는 경로를 고려해라. 이 경로는 명백히 그림 10에서 CM에 의해 취해지는 경로보다 더 길다. 따라서, 그 FORCE가 center에 벗어나서 적용될 때, 좀 더 많은 work가 처리된다. 왜냐하면 force가 적용되는 점 p가 CM에 적용될 때 보다 더 많은 경로를 그린다.
댓글 없음:
댓글 쓰기