2.1 Insertion sort
2.2 Analyzing algorithms
2.3 Designing algorithms
2.1 Insertion Sort
The numbers that we wish to sort are also known as the keys.
What separates pseudocode from "real" code is that in pseudocode, we employ whatever expressive method is most clear and concise to specify a given algorithm. Sometimes, the clearest method is English, so do not be suprised if you come across an English phrase or sentence embedded within a section of "real" code. Another difference between pseudocode and real code is that pseudocode is not typically concerned with issues of software engineering.
We start with insertion sort, which is an efficient algorithm for sorting a small number of elements. Insertion sort works the way many people sort a hand of playing cards. We start with an empty left hand and the cards face down on the table. We then remove one card at a time from the table and insert it into the correct position in the left hand. To find the correct position for a card, we compare it with each of the cards already in the hand, from right to left, as illustrated in Figure 2.1. At all times, the cards held in the left hand are sorted, and these cards were originally the top cards of the pile on the table.
pseudocode: the range of array in pseudocode starts from 1.
INSERTION-SORT(A) 1 for j = 2 to A.length 2 key = A[j] 3 // Insert A[j] into the sorted sequence A[1.. j-1]. 4 i = j - 1 5 while i > 0 and A[i] > key 6 A[i + 1] = A[i] 7 i = i - 1 8 A[i + 1] = key
code: (Notice the range of array index)
template<class T> void insertion_sort(vector<T>& A) { for (int j = 1; j < A.size(); ++j) { T key = A[j]; int i = j - 1; while (i >= 0 && A[i] > key) { A[i + 1] = A[i]; i = i - 1; } A[i + 1] = key; } }
The index j indicates the "current card" being inserted into the hand. At the beginning of each iteration of the for loop, which is indexed by j, the subarray consisting the elements A[1... j - 1] contitutes the currently sorted hand, and the remaining subarray
A[j + 1 ... n] corresponds to the pile of cards still on the table.
In fact, elements A[1.. j - 1] are the elements originally in positions 1 through j - 1, but now in sorted order. We state these properties of A[1.. j - 1] formally as a loop invariant:
At the start of each iteration of the for loop of lines 1-8, the subarray A[1..j-1] consists of the elements originally in A[1.. j - 1], but in sorted order.
We use loop invariants to help us understand why an algorithm is correct. we must show three things about a loop invariant:
- Initialization : It is true prior to the first iteration of the loop.
- Maintenance : If it is true before an iteration of the loop, it remains true before the next iteration.
- Termination : When the loop terminates, the invariant gives us a useful property that helps show that the algorithm is correct
When the first two properties hold, the loop invariant is true prior to every iteration of the loop.
The third property is perhaps the most important one, since we are using the loop invariant to show correct ness. Typically, we use the loop invariant along with the condition that caused the loop to terminate. The termination property differs from how we usually use mathematical induction, in which we apply the inductive step infinitely; here, we stop the "induction" when the loop terminates.
Pseudocode conventions
- Variables (such as i, j, and key) are local to the given procedure. We shall not use global variables without explicit indication.
Exercises
2.1 - 1 : Using Figure 2.2 as a model, illustrate the operation of INSERTION-SORT on the array A = <31, 41, 59, 26, 41, 58>.
31, 41, 59, 26, 41, 58
26, 31, 41, 59, 41, 58
26, 31, 41, 41, 59, 58
26, 31, 41, 41, 58, 59
2.1. - 2 : Rewrite the INSERTION-SORT procedure to sort into nonincreasing instead of non-decreasing order.
pseudocode: the range of array in pseudocode starts from 1.
INSERTION-SORT(A) 1 for j = 2 to A.length 2 key = A[j] 3 // Insert A[j] into the sorted sequence A[1.. j-1]. 4 i = j - 1 5 while i > 0 and A[i] < key 6 A[i + 1] = A[i] 7 i = i - 1 8 A[i + 1] = key
code: (Notice the range of array index)
template<class T> void insertion_sort(vector<T>& A) { for (int j = 1; j < A.size(); ++j) { T key = A[j]; int i = j - 1; while (i >= 0 && A[i] < key) { A[i + 1] = A[i]; i = i - 1; } A[i + 1] = key; } }
2.1 - 3 : Consider the searching problem :
Input : A sequence of n numbers A = <a1, a2, ... , an> and a value v.
Output : An index i such that v = A[i] or the special value NIL if v doest not appear in A.
write pseudocode for linear search, which scans through the sequence, looking for v. Using a loop invariant, prove the your algorithm is correct. Make sure that your loop invariant fulfills the three necessary properties.
just use for loop, using if statement if(A[i] == v).
2.1 - 4 : Consider the problem of adding two n-bit binary integers, stored in two n-element arrays A and B. The sum of the two integers should be stored in binary form in an (n+1) - element array C. State the problem formally and write pseudocode for adding the two integers.
When you do the binary addition, you have to care the form of the binary numer, such as the complement, sign bit and so on. In addition, You need to take care of the length of two binary numbers. If the lengths of two binary numbers are different, you need to balance the addition place between two numbers.
So the simple pseudocode is:
1 find the length of each bit array.
2 Check the sign bit of each bit array.
3 add each element of the binary with the larger length with the each element of the binary with the smaller length, adjusting the location of each bit index.
4 and then, you need to handle the overflow problems : positive + positive, negative + negative, positive + negative
2.2 Analyzing algorithms
Analyzing an algorithm has come to mean predicting the resources that the algorithm requires. Occasionally, resources such as memory, communication band-width, or computer hardware are of primary concern, but most often it is computational time that we want to measure.
The RAM model contains instructions commonly found in real computers: arithmetic (such as add, subtract, multiply, divide, remainder, floor, ceiling), data movement (load, store, copy), and control (conditional and unconditional branch, subroutine call and return). Each such instruction takes a constant amount of time.
In most computers, shifting the bits of an integer by one position to the left is equivalent to multiplication by 2, so that shifting the bits by k positions to the left is equivalent to multiplication by 2^k. Therefore, such computers can compute 2^k in one constant-time instruction by shifting the integer 1 by k position the left, as long as k is no more than the number of bits in a computer word.
Analysis of insertion sort
To analyze, we need to define the terms "running time" and "size of input" more carefully.
The best notion for input size depends on the problem being studied. .. array size n for sorting. the total number of bits needed to represent the input in ordinary binary notation for multiplying two integers. the vertices and edges in the graph.
The running time of an algorithm on a particular input is the number of primitive operations or "steps" executed. It is convenient to define the notion of step so that it is as machine-independent as possible.
for best case, linear function of n
T(n) = c1n + c2(n-1) + c4(n-1) + c5(n-1) +c8(n-1)
= (c1 + c2 + c4 + c5 + c8)n - (c2 + c4 + c5 + c8)
for worst case, quadratic function of n
T(n) = (c5/2 + c6/2 + c7/2)n^2 + (c1 + c2 + c4 + c5/2 -c6/2 - c7/2 + c8)n - (c2 + c4+ c5+ c8)
For the remainder of this book, though, we shall usually concentrate on finding only the worst-case running time, that is, the longest running time for any input of size n. We give three reasons for this orientation.
- The worst-case running time of an algorithm gives us an upper bound on the running time for any input. Knowing it provides a guarantee that the algorith will never take any longer.
- For some algorithms, the worst case occurs fairly often. ex) database searching
- The "average case" is often roughly as bad as the worst case.
In some particular case, we shall be interested in the average-case running time of an algorithm; we shall see the technique of probabilistic analysis applied to various algorithms throughout this book.
Order of Growth
We shall now make one more simplifying abstraction : it is the rate of growth, or order of growth, of the running time that really interests us. We therefore consider only the leading term of a formula (e.g., an^2), since the lower-order terms are relatively insignificant for large values of n. We also ignore the leading term's constant coefficient, since constant factors are less significant that the rate of growth in determining computational efficiency for large inputs. ... We write that insertion sort has a worst-case running time Θ(n^2) (pronounced "theta of n-squared"). We shall use Θ-notation informally in this chapter, and we will define it precisely in Chapter 3.
We usually consider one algorithm to be more efficient than another if its worst case running time has a lower order of growth.
Exercises
2.2-1 : Express the function n^3 / 1000 - 100n^2 - 100n + 3 in terms of Θ-notation
Θ(n^3)
2.2-2 : Consider sorting n numbers stored in array A by first finding the smallest element of A and exchanging it with the element in A[1]. Then find the second smallest element of A, and exchange it with A[2]. Continue in this manner for the first n - 1 elements of A. Write pseudocode for this algorithm, which is known as selection sort. What loop invariant does this algorithm maintain? Why does it need to run for only the first n - 1 elements, rather than for all n elements? Give the best-case and worst-case runing times of selection sort in Θ-notation.
pseudocode:
SELECTION-SORT(A) 1 for i = 1 to A.length-1 2 smallest = i 3 for j = i + 1 to A.length 4 if A[smallest] > A[j] 5 smallest = j 6 temp = A[smallest] 7 A[smallest] = A[i] 8 A[i] = temp
code:
template<class T> void selection_sort(vector<T>& A) { for (int i = 0; i < A.size() - 1; ++i) { int smallest = i; for (int j = i + 1; j < A.size(); ++j) if (A[smallest] > A[j]) smallest = j; int temp = A[smallest]; A[smallest] = A[i]; A[i] = temp; } }
1) What loop invariant does this algorithm maintain?
on the line 3 to 5, we can find the minimum value of array indexed from i to A.length. So, after those lines, A[i] always get the minimum value on the range. For the first iteration, the i is 0. It means that the A[i] get the minimum value of all elements in A. and then, the next iteration will give the A[i] the second minimum value of all elements in A. because It searches from 2 to A.length in A with the minimum value in all elements being in A[1].
2) Why does it need to run for only the first n - 1 elements rather than for all n elements?
Because of the algorithm. the array A is already sorted on the moment when A[n -1] gets the minimum value.
3) Give the best-case and worst-case running times of selection sort in Θ-notation.
regardless of a case, this algorithm is always Θ(n^2). Because the inner loop steps n, n-1, ... 1 time as the procedure progresses. And the outer loop performs n-1 times. So, it could be Θ(n^2).
2.2-3 : Consider linear search again (see Exercise 2.1-3). How many elements of the input sequence need to be checked on the average, assuming that the element being searched for is equally likely to be any element in the array? How about in the worst case? What are the average-case and worst-case running times of linear search in Θ-notation? Justify your answers.
the Θ-notation of linear search is Θ(n)
the average is around n/2.
2.2-4 : How can we modify almost any algorithm to have a good best-case running time?
If there is a special condition, just output the pre-computed value.
2.3 Designing algorithms
We can choose from a wide range of algorithm design techniques. For insertion sort, we used an incremental approach: having sorted the subarray A[1 .. j - 1], we inserted the single element A[j] into its proper value, yielding the sorted subarray A[1...j].
In this section, we examine an alternative design approach, known as "divide-and-conquer," which we shall explore in more detail in Chapter 4. We'll use divide-and-conquer to design a sorting algorithm whose worst-case running time is much less than that of insertion sort. One advantage of divide-and-conquer algorithms is that their running times are often easily determined using techniques that we will see in Chapter 4.
2.3.1 The divide-and-conquer approach
Many useful algorithms are recursive in structure: to solve a given problem, they call themselves recursively one or more times to deal with closely related sub-problems. These algorithms typically follow a divide-and-conquer approach : they break the problem into several subproblems that are similar to the origin problem but smaller in size, solve the subproblems recursively, and then combine these solutions to create a solution to the original problem.
The divide-and-conquer paradigm involves three steps at each level of the recursion:
code:
Lines 10-18 (pseucode), illustrated in Figure 2.3, perform the r-p+1 basic steps by maintaining the following loop invariant:
At the start of each iteration of the for loop of lines 12-18, the subarray A[p.. k-1] contains the k - p smallest elements of L[1.. n1 + 1] and R[1..n2 +1], in sorted order. Moreover, L[i] and R[j] are the smallest elements of their arrays that have not been copied back into A
Initialization : Prior to the first iteration of the loop, we have k = p, so that the subarray A[p ..k - 1] is empty. This empty subarray contains the k - p = 0 smallest elements of L and R, and sice i = j = 1, both L[i] and R[j] are the smallest elements of their arrays that have not been copied back into A.
Maintenance : To see that each iteration maintains the loop invariant, let us first suppose that L[i] <= R[j]. Then L[i] is the smallest element not yet copied back into A. Because A[p.. k - 1] contains the k - p smallest elements after the line 14 copies L[i] into A[k], the subarray A[p..k] will contain the k - p + 1 smallest elements. Incrementing k (in the for loop update) and i (in line 15) reestablishes the loop invariant for the next iteration. If instead L[i] > R[j], then lines 17-18 perform the appropriate action to maintain the loop invariant.
Termination : At termination, k = r + 1. By the loop invariant, the subarray A[p.. k - 1], which is A[p..r], contains the k - p = r - p + 1 smallest elements of L[1.. n1 + 1] and R[1..n2 + 1], in sorted order. The arrays L and R together contain n1 + n2 +2 = r - p +3 elements. All but the two largest have been copied back into A, and these two largest elements are the sentinels.
To see that the MERGE procedure runs in Θ(n) time, where n = r - p + 1, observe that each of lines 1-3 and 8 - 11 takes constant time, the for loops of lines 4-7 take Θ(n1 + n2) = Θ(n) time, and there are n iterations of the for loop of lines 12-18, each of which takes constant time.
We can now use the MERGE procedure as a subroutine in the merge sort algorithm. The procedure MERGE-SORT(A, p, r) sorts the elements in the subarray A[p..r]. If p>= r, the subarray has at most one element and is therefore already sorted, Otherwise, the divide step simply computes an index q that partions A[p..r] into two subarrays: A[p..q], containing [n/2] elements, and A[q+1..r], containing [n/2 elements.
pseudocode:
code:
To sort the entire sequence A = <A[1], ... A[n]>, we make the intial call MERGE-SORT(A, 1, A.length), where once angain A.length = n.
2.3.2 Analyzing divide-and-conquer algorithms
When an algorithm contains a a recursive call to itself, we can often describe its running time by a recurrence equation or recurrence, which describes the overall running time on a problem of size n in terms of the running time on smaller inputs. We can then use mathematical tools to solve the recurrence and provide bounds on the performance of the algorithm
A recurrence for the running time of a divide-and-conquer algorithm falls out from the three steps of the basic paradigm. As before, we let T(n) be the running time on a problem of size n. If the problem size is small enough, say n <= c for some contant c, the straightforward solution takes constant time, which we write as Θ(1). Suppose that our division of the problem yields a subproblems, each of which is 1/b the size of original. (For merge sort, both a and b are 2, but we shall see many divide-and-conquer algorithms in which a != b.) It takes time T(n/b) to solve one subproblem of size n/b, and so it takes time aT(n/b) to solve a of them. If we take D(n) time to divide the problem into subproblems and C(n) time to combine the soultions to the sub problems into the solution to the original problem, we get the recurrence
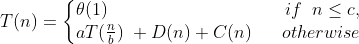
In chapter 4, we shall see how to solve common recurrences of this form.
Analysis of merge sort
... When we have n > 1 elements, we break down the running time as follows.
Divide : The divide step just computes the middle of the subarray, which takes constant time. Thus, D(n) = Θ(1).
Conquer : We recursively solve two subproblems, each of size n/2, which contributes 2T(n/2) to the running time.
Combine : We have already noted that the MERGE procedure on an n-element subarray takes time Θ(n), and so C(n) = Θ(n).
When we add the function D(n) and C(n) for the merge sort analysis, we are adding a function that is Θ(n) and a function that is Θ(1). This sum is a linear function of n, that is, Θ(n). Adding it to the 2T(n/2) term from the "conquer" step gives the recurrence for the worst-case running time T(n) of merge sort:
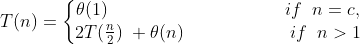
In Chapter 4, we shall see the "master theorem," which we can use to show that T(n) is Θ(nlg(n)), where lg(n) stands for log_2(n). Because the logarithm function grows more slowly than any linear function, for large enough inputs, merge sort, with its Θ(nlg(n)) running time, outperforms insertion sort, whose running time is Θ(n^2), in the worst case.
We do not need the master theorem to intuitively understand why the solution to the recurrence (2.1) is T(n) = Θ(nlg(n)). Let us rewrite recurrence (2.1) as
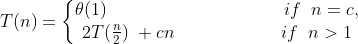
where the constant c represents the time required to solve problem of size 1 as well as the time per array element of divide and combine steps.
Figure 2.5 How to construct a recursion tree for the recurrence T(n) = 2T(n/2) + cn. Part (a) shows T(n), which progressively expands in (b) - (d) to form the recursion tree. The fully expanded tree in part (d) has lg(n) + 1 levels (i.e., it has height lg(n), as indicated), and each level contributes a total cost of cn. The total cost, therefore, is cnlg(n) + cn, which is Θ(nlg(n)).
Exercoses
2.3-1 : Using Figure 2.5 as a model, illustrate the operation of merge sort on the array A = <3, 41, 52, 26, 38, 57, 9, 49>.
The length of A is 8. So, the parameters of Merge Sort shoulbe 0, 7.
and then the middle one (0 + 7) / 2 = 3.5 -> 3
So,
MergeSort(0, 3)
MergeSort(4, 7)
Merge(0, 3, 7)
the MergeSort(0,3) results in
MergeSort(0, 1)
MergeSort(1, 3)
Merge(0, 1, 3)
and then, MergeSort(0,1) results in MergeSort(0,0). But since the condition p < r prevent the progress, it stops. and then, MergeSort(1,3) results in MergeSort(1,1) but this also stops. So, Merge(0,1,3) will perform.
In this way, the array A will be sorted.
2.3-2 : Rewrite the MERGE procedure so that it does not use sentinels, instead stopping once either array L or R has had all its elements copied back to A and then copying the remainder of the other array back into A.
code:
2.3-3 : Use mathematical induction to show that when n is an exact power of 2, the solution of the recurrence
T(n) = 1) 2 if n = 2,
2) 2T(n/2) + n if n = 2^k, for k > 1
is T(n) = nlg(n).
You can just use the same process of analyzing the merge sort.
2.3-4 : We can express insertion sort as a recursive procedure as follows. In order to sort A[1..n], we recursively sort A[1.. n-1] and then insert A[n] into the sorted array A[1.. n-1]. Write a recurrence for the running time of this recursive version of insertion sort.
2.3-5 : Referring back to the searching problem (see Exercise 2.1-3), observe that if the sequence A is sorted, we can check the midpoint of the sequence against v and elminate half of the sequence from further consideration. The binary search algorithm repeats this procedure, halving the size of the remaining portion of the sequence each time. Write pseudocode, either iterative or recursive, for binary search. Argue that the worst-case running time of binary search is Θ(lg(n)).
2.3-6 : Observe that the while loop of linees 5-7 of the INSERTION-SORT procedure in Section 2.1 uses a linear search to scan (backward) through the sorted subarray A[1..j-1]. Can we use a binary search (see Exercise 2.3-5) instead to improve the overall worst-case running time of insertion sort to Θ(nlg(n))?
No. Because we have to shift the bigger elements to the right. We can find the position to insert the key, but we anyway shift all the bigger elements to the right.
2.3-7 : Describe a Θ(nlg(n)) - time algorithm that, give a set S of n integers and another integer x, determines whether or not there exist two elements in S whose sum is exactly x.
Problems
2-1 Insertion sort on small arrays in merge sort
Although merge sort runs in Θ(nlg(n)) worst-case time and insertion sort runs in Θ(n^2) wost-cast time, the constant factors in insertion sort can make it faster in practice for small problem sizes on many machines. Thus, it make sense to coarsen the leaves of the recursion by using insertion sort within merge sort when subproblems become sufficiently small. Consider a modification to merge sort in which n/k sublists of length k are sorted using insertion sort and then merged using the standard merging mechanism, where k is a value to be determined.
I have to referred the solutions, because this kind of problems is hard for me.
a. Show that insertion sort can sort the n/k sublists, each of length k, in Θ(nk) worst-case time.
Insertion sort takes Θ(k^2) time per k-element in the worst case. Therefore, sorting n/k lists of k elements each takes Θ(k^2 n / k = Θ(nk) worst-case tiem
b. Show how to merge the sublists in Θ(nlg(n/k)) worst-case time.
Θ(n ㆍ(n/k)) = Θ(n^2 / k)
the n is from copying each element once into the result list, n/k from examining n/k lists at each step to select next itme for result list.
To achieve Θ(nlg(n/k)) - time merging, we merge the lists pairwise, then merge the resulting lists pairwise, and so on, until there's just one list. The pairwise merging requires Θ(n) work at each level, since we are still working on n elements, even if they are partitioned among sublists. The number of levels, starting with n/k lists (with k elements each) and finishing with 1 list (with n elements), is [lg(n/k)]. Therefore, the total running time for the merging is Θ(nlg(n/k)).
I think I should pass this problem now, and look back on this after chapter 3.
2-2 Correctness of bubblesort
Bubblesort is a popular, buf inefficient, sorting algorithm. It works by repeatedly swapping adjacent elements that are out of order.
a. Let A' denote the output of BUBBLESORT(A). To prove that BUBBLESORT is correct, we need to prove that it terminates and that A'[1] <= A'[2] <= ... <= A'[n],
where n = A.length. In order to show that BUBBLESORT actually sorts, what else do we need to prove?
According to the solution, it says, we need to show that the elements of A' form a permutation of the elements of A.
But I don't know why the solution says in the way. I think showing the Loop invariant is just things to prove the algorithm.
After looking at the b, I can know why the solution says that way.
b. State precisely a loop invariant for the for loop in lines 2-4, and prove that this loop invariant holds. Your proof should use the structure of the loop invariant proof presented in this chapter.
Loop Invariant : At the start of each iteration of the for loop of lines 2-4,
A[j] = min[A[k]: j<=k <=n] and the subarray A[j..n] is a permutation of the values that were in A[j..n] at the time that the loop started.
Initialization : Initially,, j = n, and the subarray A[j.. n] consists of single element A[n]. The loop invariant trivially holds.
Maintenance : As the loop goes forward, the range of j is chainging. I mean on lines 3 ~4, the lines extends the range. So, if A[j] is smaller than A[j-1], both are exchanged, and A[j-1] should be smaller. Thus, the A[j-1] is min[A[k]: j - 1 <= k <= n] and the subarray A[j-1 .. n ] is a permutation of the values in A[j-1..n].
Termination : The loop terminates when j reaches i. By the statement of the loop invariant, A[i] = min[A[k] : i <= k <=n] and A[i..n] is a permutation of the values that were in A[i..n] at the time that the loop started.
on the line 3 to 5, we can find the minimum value of array indexed from i to A.length. So, after those lines, A[i] always get the minimum value on the range. For the first iteration, the i is 0. It means that the A[i] get the minimum value of all elements in A. and then, the next iteration will give the A[i] the second minimum value of all elements in A. because It searches from 2 to A.length in A with the minimum value in all elements being in A[1].
2) Why does it need to run for only the first n - 1 elements rather than for all n elements?
Because of the algorithm. the array A is already sorted on the moment when A[n -1] gets the minimum value.
3) Give the best-case and worst-case running times of selection sort in Θ-notation.
regardless of a case, this algorithm is always Θ(n^2). Because the inner loop steps n, n-1, ... 1 time as the procedure progresses. And the outer loop performs n-1 times. So, it could be Θ(n^2).
2.2-3 : Consider linear search again (see Exercise 2.1-3). How many elements of the input sequence need to be checked on the average, assuming that the element being searched for is equally likely to be any element in the array? How about in the worst case? What are the average-case and worst-case running times of linear search in Θ-notation? Justify your answers.
the Θ-notation of linear search is Θ(n)
the average is around n/2.
2.2-4 : How can we modify almost any algorithm to have a good best-case running time?
If there is a special condition, just output the pre-computed value.
2.3 Designing algorithms
We can choose from a wide range of algorithm design techniques. For insertion sort, we used an incremental approach: having sorted the subarray A[1 .. j - 1], we inserted the single element A[j] into its proper value, yielding the sorted subarray A[1...j].
In this section, we examine an alternative design approach, known as "divide-and-conquer," which we shall explore in more detail in Chapter 4. We'll use divide-and-conquer to design a sorting algorithm whose worst-case running time is much less than that of insertion sort. One advantage of divide-and-conquer algorithms is that their running times are often easily determined using techniques that we will see in Chapter 4.
2.3.1 The divide-and-conquer approach
Many useful algorithms are recursive in structure: to solve a given problem, they call themselves recursively one or more times to deal with closely related sub-problems. These algorithms typically follow a divide-and-conquer approach : they break the problem into several subproblems that are similar to the origin problem but smaller in size, solve the subproblems recursively, and then combine these solutions to create a solution to the original problem.
The divide-and-conquer paradigm involves three steps at each level of the recursion:
- Divide the problem into a number of subproblems that are smaller instances of the same problem.
- Conquer the subproblems by solving them recursively. If the subproblems sizes are small enough, however, just solve the subproblems in a straightforward manner.
- Combine the solutions to the subproblems into the solution for the original problem.
The merge sort algorithm closely follows the divide-and-conquer paradigm. Intuitively, it operates as follows.
- Divide : Divide the n-element sequence to be sorted into two subsequences of n/2 elements each
- Conquer : Sort the two subsequences recursively using merge sort.
- Combine : Merge the two sorted subsequence to produce the sorted answer.
The recursion "bottoms out" when the sequence to be sorted has length 1, in which case there is no work to be done, since every sequence of length 1 is already in sorted order.
They key operation of the merge sort algorithm is the merging of two sorted sequences in the "combine" step. We merge by calling an auxiliary procedure MERGE(A, p, q, r), where A is a an array and p,q, and r are indices into the array such that p <= q < r. The procedure assumes that the subarrays A[p .. q] and A[q + 1.. r] are in sorted order. It merges them to form a single sorted subarray that replaces the current subarray A[p..r].
Our MERGE procedure takes time Θ(n), where n = r - p + 1 is the total number of elements being merged, and it works as follows. Returning to our card playing motif, suppose we have two piles of cards face up on a table. Each pile is sorted, with the smallest cards on top. We wish to merge the two piles into a single sorted output pile, which is to be face down on the table. Our basic step consists of choosing the smaller of the two cards on top of the face-up piles, removing it from its pile (which exposes a new top card), and placing this card face down onto the output pile. We repeat this step until one input pile is empty, at which time we just take the remaining input pile and place it face down onto the output pile. ... Since we perform at most n basic steps, merging takes Θ(n) time.
pseudocode:
MERGE(A,p,q,r) 1 n1 = q - p + 1 2 n2 = r - q 3 let L[1.. n1 + 1] and R[1..n2 + 1] be new arrays 4 for i = 1 to n1 5 L[i] = A[p + i -1] 6 for j = 1 to n2 7 R[j] = A[q+ j] 8 L[n1 + 1] = INFINITY 9 R[n2 + 1] = INFINITY 10 i = 1 11 j = 1 12 for k = p to r 13 if L[i] <= R[j] 14 A[k] = L[i] 15 i = i + 1 16 else 17 A[k] = R[j] 18 j = j + 1
code:
// Add 1 to prevent the wrong indexing int L[SIZE / 2 + 1]; int R[SIZE / 2 + 1]; template<class T> void merge(vector<T>& A, int p, int q, int r) { int n1 = q - p + 1; int n2 = r - q; for (int i = 0; i < n1; ++i) L[i] = A[p + i]; for (int j = 0; j < n2; ++j) R[j] = A[q + j + 1]; L[n1] = intmax; R[n2] = intmax; int i = 0, j = 0; for (int k = p; k <= r; ++k) { if (L[i] <= R[j]) { A[k] = L[i]; ++i; } else { A[k] = R[j]; ++j; } } }
Lines 10-18 (pseucode), illustrated in Figure 2.3, perform the r-p+1 basic steps by maintaining the following loop invariant:
At the start of each iteration of the for loop of lines 12-18, the subarray A[p.. k-1] contains the k - p smallest elements of L[1.. n1 + 1] and R[1..n2 +1], in sorted order. Moreover, L[i] and R[j] are the smallest elements of their arrays that have not been copied back into A
Initialization : Prior to the first iteration of the loop, we have k = p, so that the subarray A[p ..k - 1] is empty. This empty subarray contains the k - p = 0 smallest elements of L and R, and sice i = j = 1, both L[i] and R[j] are the smallest elements of their arrays that have not been copied back into A.
Maintenance : To see that each iteration maintains the loop invariant, let us first suppose that L[i] <= R[j]. Then L[i] is the smallest element not yet copied back into A. Because A[p.. k - 1] contains the k - p smallest elements after the line 14 copies L[i] into A[k], the subarray A[p..k] will contain the k - p + 1 smallest elements. Incrementing k (in the for loop update) and i (in line 15) reestablishes the loop invariant for the next iteration. If instead L[i] > R[j], then lines 17-18 perform the appropriate action to maintain the loop invariant.
Termination : At termination, k = r + 1. By the loop invariant, the subarray A[p.. k - 1], which is A[p..r], contains the k - p = r - p + 1 smallest elements of L[1.. n1 + 1] and R[1..n2 + 1], in sorted order. The arrays L and R together contain n1 + n2 +2 = r - p +3 elements. All but the two largest have been copied back into A, and these two largest elements are the sentinels.
To see that the MERGE procedure runs in Θ(n) time, where n = r - p + 1, observe that each of lines 1-3 and 8 - 11 takes constant time, the for loops of lines 4-7 take Θ(n1 + n2) = Θ(n) time, and there are n iterations of the for loop of lines 12-18, each of which takes constant time.
We can now use the MERGE procedure as a subroutine in the merge sort algorithm. The procedure MERGE-SORT(A, p, r) sorts the elements in the subarray A[p..r]. If p>= r, the subarray has at most one element and is therefore already sorted, Otherwise, the divide step simply computes an index q that partions A[p..r] into two subarrays: A[p..q], containing [n/2] elements, and A[q+1..r], containing [n/2 elements.
pseudocode:
MERGE-SORT(A,p,r) 1 if p < r 2 q = [(p + r) / 2] 3 MERGE-SORT(A,p,q) 4 MERGE-SORT(A,q + 1, r) 5 MERGE(A, p, q, r)
code:
template<class T> void merge_sort(vector<T>& A, int p, int r) { if (p < r) { int q = (p + r) / 2; merge_sort(A, p, q); merge_sort(A, q + 1, r); merge(A, p, q, r); } }
To sort the entire sequence A = <A[1], ... A[n]>, we make the intial call MERGE-SORT(A, 1, A.length), where once angain A.length = n.
2.3.2 Analyzing divide-and-conquer algorithms
When an algorithm contains a a recursive call to itself, we can often describe its running time by a recurrence equation or recurrence, which describes the overall running time on a problem of size n in terms of the running time on smaller inputs. We can then use mathematical tools to solve the recurrence and provide bounds on the performance of the algorithm
A recurrence for the running time of a divide-and-conquer algorithm falls out from the three steps of the basic paradigm. As before, we let T(n) be the running time on a problem of size n. If the problem size is small enough, say n <= c for some contant c, the straightforward solution takes constant time, which we write as Θ(1). Suppose that our division of the problem yields a subproblems, each of which is 1/b the size of original. (For merge sort, both a and b are 2, but we shall see many divide-and-conquer algorithms in which a != b.) It takes time T(n/b) to solve one subproblem of size n/b, and so it takes time aT(n/b) to solve a of them. If we take D(n) time to divide the problem into subproblems and C(n) time to combine the soultions to the sub problems into the solution to the original problem, we get the recurrence
In chapter 4, we shall see how to solve common recurrences of this form.
Analysis of merge sort
... When we have n > 1 elements, we break down the running time as follows.
Divide : The divide step just computes the middle of the subarray, which takes constant time. Thus, D(n) = Θ(1).
Conquer : We recursively solve two subproblems, each of size n/2, which contributes 2T(n/2) to the running time.
Combine : We have already noted that the MERGE procedure on an n-element subarray takes time Θ(n), and so C(n) = Θ(n).
When we add the function D(n) and C(n) for the merge sort analysis, we are adding a function that is Θ(n) and a function that is Θ(1). This sum is a linear function of n, that is, Θ(n). Adding it to the 2T(n/2) term from the "conquer" step gives the recurrence for the worst-case running time T(n) of merge sort:
In Chapter 4, we shall see the "master theorem," which we can use to show that T(n) is Θ(nlg(n)), where lg(n) stands for log_2(n). Because the logarithm function grows more slowly than any linear function, for large enough inputs, merge sort, with its Θ(nlg(n)) running time, outperforms insertion sort, whose running time is Θ(n^2), in the worst case.
We do not need the master theorem to intuitively understand why the solution to the recurrence (2.1) is T(n) = Θ(nlg(n)). Let us rewrite recurrence (2.1) as
where the constant c represents the time required to solve problem of size 1 as well as the time per array element of divide and combine steps.
Figure 2.5 How to construct a recursion tree for the recurrence T(n) = 2T(n/2) + cn. Part (a) shows T(n), which progressively expands in (b) - (d) to form the recursion tree. The fully expanded tree in part (d) has lg(n) + 1 levels (i.e., it has height lg(n), as indicated), and each level contributes a total cost of cn. The total cost, therefore, is cnlg(n) + cn, which is Θ(nlg(n)).
Exercoses
2.3-1 : Using Figure 2.5 as a model, illustrate the operation of merge sort on the array A = <3, 41, 52, 26, 38, 57, 9, 49>.
The length of A is 8. So, the parameters of Merge Sort shoulbe 0, 7.
and then the middle one (0 + 7) / 2 = 3.5 -> 3
So,
MergeSort(0, 3)
MergeSort(4, 7)
Merge(0, 3, 7)
the MergeSort(0,3) results in
MergeSort(0, 1)
MergeSort(1, 3)
Merge(0, 1, 3)
and then, MergeSort(0,1) results in MergeSort(0,0). But since the condition p < r prevent the progress, it stops. and then, MergeSort(1,3) results in MergeSort(1,1) but this also stops. So, Merge(0,1,3) will perform.
In this way, the array A will be sorted.
2.3-2 : Rewrite the MERGE procedure so that it does not use sentinels, instead stopping once either array L or R has had all its elements copied back to A and then copying the remainder of the other array back into A.
code:
int one[SIZE]; template<class T> void merge(vector<T>& A, int p, int q, int r) { int i = p; int j = q + 1; int cursor = p; while (i <= q || j <= r) { if (i == q + 1) { one[cursor] = A[j]; ++j; } else if (j == r + 1) { one[cursor] = A[i]; ++i; } else if (A[i] <= A[j]) { one[cursor] = A[i]; ++i; } else { one[cursor] = A[j]; ++j; } ++cursor; } for (int i = p; i <= r; ++i) A[i] = one[i]; }
2.3-3 : Use mathematical induction to show that when n is an exact power of 2, the solution of the recurrence
T(n) = 1) 2 if n = 2,
2) 2T(n/2) + n if n = 2^k, for k > 1
is T(n) = nlg(n).
You can just use the same process of analyzing the merge sort.
2.3-4 : We can express insertion sort as a recursive procedure as follows. In order to sort A[1..n], we recursively sort A[1.. n-1] and then insert A[n] into the sorted array A[1.. n-1]. Write a recurrence for the running time of this recursive version of insertion sort.
template <class T> void insertion_sort_recursive(vector<T>& A, int key_index, int array_size) { if (key_index >= array_size) return; T key = A[key_index]; int i = key_index - 1; while (i >= 0 && A[i] > key) { A[i + 1] = A[i]; --i; } A[i + 1] = key; insertion_sort_recursive(A, key_index + 1, array_size); }
2.3-5 : Referring back to the searching problem (see Exercise 2.1-3), observe that if the sequence A is sorted, we can check the midpoint of the sequence against v and elminate half of the sequence from further consideration. The binary search algorithm repeats this procedure, halving the size of the remaining portion of the sequence each time. Write pseudocode, either iterative or recursive, for binary search. Argue that the worst-case running time of binary search is Θ(lg(n)).
BINARY-SEARCH-RECURSIVE(A, START, END, KEY) if START > END return NIL MID = (START + END) / 2 if A[MID] == KEY return MID else if A[MID] > KEY return BINARY-SEARCH-RECURSIVE(A, START, MID - 1, KEY) else return BINARY-SEARCH-RECURSIVE(A, MID + 1, END, KEY)
BINARY-SEARCH-ITERATIVE(A, KEY) start = 1 end = A.length while start <= end mid = (start + end) / 2 if A[mid] == KEY return mid else if A[mid] > KEY end = mid - 1 else start = mid + 1 return NIL
2.3-6 : Observe that the while loop of linees 5-7 of the INSERTION-SORT procedure in Section 2.1 uses a linear search to scan (backward) through the sorted subarray A[1..j-1]. Can we use a binary search (see Exercise 2.3-5) instead to improve the overall worst-case running time of insertion sort to Θ(nlg(n))?
No. Because we have to shift the bigger elements to the right. We can find the position to insert the key, but we anyway shift all the bigger elements to the right.
2.3-7 : Describe a Θ(nlg(n)) - time algorithm that, give a set S of n integers and another integer x, determines whether or not there exist two elements in S whose sum is exactly x.
template <class T> pair<int,int> find_twosum(const vector<T>& A, T key) { merge_sort(A, 0, A.size() -1) for (int i = 0; i < A.size(); ++i) { T left = A[i]; T find = key - left; int exist = binary_search(A, find); if (exist != -1) return make_pair(i, exist); } return make_pair(0,0); }
Problems
2-1 Insertion sort on small arrays in merge sort
Although merge sort runs in Θ(nlg(n)) worst-case time and insertion sort runs in Θ(n^2) wost-cast time, the constant factors in insertion sort can make it faster in practice for small problem sizes on many machines. Thus, it make sense to coarsen the leaves of the recursion by using insertion sort within merge sort when subproblems become sufficiently small. Consider a modification to merge sort in which n/k sublists of length k are sorted using insertion sort and then merged using the standard merging mechanism, where k is a value to be determined.
I have to referred the solutions, because this kind of problems is hard for me.
a. Show that insertion sort can sort the n/k sublists, each of length k, in Θ(nk) worst-case time.
Insertion sort takes Θ(k^2) time per k-element in the worst case. Therefore, sorting n/k lists of k elements each takes Θ(k^2 n / k = Θ(nk) worst-case tiem
b. Show how to merge the sublists in Θ(nlg(n/k)) worst-case time.
Θ(n ㆍ(n/k)) = Θ(n^2 / k)
the n is from copying each element once into the result list, n/k from examining n/k lists at each step to select next itme for result list.
To achieve Θ(nlg(n/k)) - time merging, we merge the lists pairwise, then merge the resulting lists pairwise, and so on, until there's just one list. The pairwise merging requires Θ(n) work at each level, since we are still working on n elements, even if they are partitioned among sublists. The number of levels, starting with n/k lists (with k elements each) and finishing with 1 list (with n elements), is [lg(n/k)]. Therefore, the total running time for the merging is Θ(nlg(n/k)).
I think I should pass this problem now, and look back on this after chapter 3.
2-2 Correctness of bubblesort
Bubblesort is a popular, buf inefficient, sorting algorithm. It works by repeatedly swapping adjacent elements that are out of order.
BUBBLESORT(A)
1 for i = 1 to A.length - 1
2 for j = A.length downto i + 1
3 if A[j] < A[j-1]
4 exchange A[j] with A[j-1]
a. Let A' denote the output of BUBBLESORT(A). To prove that BUBBLESORT is correct, we need to prove that it terminates and that A'[1] <= A'[2] <= ... <= A'[n],
where n = A.length. In order to show that BUBBLESORT actually sorts, what else do we need to prove?
According to the solution, it says, we need to show that the elements of A' form a permutation of the elements of A.
But I don't know why the solution says in the way. I think showing the Loop invariant is just things to prove the algorithm.
After looking at the b, I can know why the solution says that way.
b. State precisely a loop invariant for the for loop in lines 2-4, and prove that this loop invariant holds. Your proof should use the structure of the loop invariant proof presented in this chapter.
Loop Invariant : At the start of each iteration of the for loop of lines 2-4,
A[j] = min[A[k]: j<=k <=n] and the subarray A[j..n] is a permutation of the values that were in A[j..n] at the time that the loop started.
Initialization : Initially,, j = n, and the subarray A[j.. n] consists of single element A[n]. The loop invariant trivially holds.
Maintenance : As the loop goes forward, the range of j is chainging. I mean on lines 3 ~4, the lines extends the range. So, if A[j] is smaller than A[j-1], both are exchanged, and A[j-1] should be smaller. Thus, the A[j-1] is min[A[k]: j - 1 <= k <= n] and the subarray A[j-1 .. n ] is a permutation of the values in A[j-1..n].
Termination : The loop terminates when j reaches i. By the statement of the loop invariant, A[i] = min[A[k] : i <= k <=n] and A[i..n] is a permutation of the values that were in A[i..n] at the time that the loop started.
댓글 없음:
댓글 쓰기