따라서, 공부를 해 나가면서 내가 몰랐던 것, 중요하게 알아야 하는 것, 긴밀하게 연결되는 것들 물리엔진 이해에 있어서 중요한 것들을 공부하여 기록할 것이다. 물론, 다른 세부사항들이 있지만, 내가 보기에 쉽다고 판단되는 것들은 생략되어 있다.
이 시리즈의 내용 구성은 나의 느낌상 소설의 액자식 구성같다. 그러니까, 비슷한 내용이 반복된다. 그렇게 된 이유는, 이 물리엔진의 기반이 되는, 처음 시초가 될 수 있는 논문이 있다고 했을 때 그 논문으로부터 다른 사람이 정리한 자료가 있고, 또 그러한 자료들을 기반으로 정리한 자료가 있을 때, 우리는 거꾸로 최근의 것에서 처음의 것으로 거슬러 올라갈려고 한다.
그러니까 논문 -> 논문으로부터 알기 쉽게 정리 -> 그 정리를 좀 더 간단하게 정리 순서를 반대로 간다는 것이다. 논문은 상대적으로 좀 더 읽고 이해하기가 어렵기 때문에, 반대로 가면서 반복하면서 공부를 한다면 이해력이 높아질 것이라 예상한다.
Introduction
1. 엔진의 구분
1) Object의 종류
- Mass-Aggregate
- RigidBody *
2) Contact Resolution
- Iterative Approach * : Good and normal and easy to implement
- Jacobian-based Approach (Simultaneous Contact Resolution) : Hard
- Reduced Coordinate Approach : normally not used.
3) Impulses and Forces
- Force-based : Jacobian, Reduced Coordinate Approach
- Impulse-based *
Part 1 Particle Physics
Chapter 2 The Mathematics of Particles
1. 벡터곱(외적)의 기하학적 의미
a의 방향에 있지 않는 b의 컴포넌트를 말한다.
2. Orthonormal Basis
정규직교 기저 찾는 방법
이면, 포기, a와 b가 평행이므로.
- Normalize(a), Normalize(b), Normalize(c)
이렇게 되는 이유는, 처음에c가 a와 b에 직교하게되고, 다음의 외적으로 b는 c와 a 직교하게 된다. 따라서 a와 b와 c가 직교하므로, 정규화를하게 되면, 정규직교 기저를찾을 수 있다.
3. Gram-Schmidt Process : R^n에서 어떤 non-zero subspace에 대해, 직교 기저를 찾는 알고리즘. 이 알고리즘이 위의 Orthonormal Basis를 찾는 방법보다 더 정확하다고 함.
R^n에 대해 정규직교 기저를 찾는 일반적인 프로세스는
다음의 연산자를 가정했을 때
u1 = v1
u2 = v2 - Proj_u1(v2)
uk = vk - sum^(k-1)_(j=1) Proj_j(vk)
가 되고
ei = vi / |vi|
라고 하면,
{e1, e2, e3, ...., ek}
가 정규직교 기저가 된다.
그런데, 일반적인 게임에서 R^3에서 연산을 수행하고. 두 개의 벡터가 주어진다고 했을 때,
다음의 코드를 통해 Gram-Schmidt Process를 이용하여 정규직교 기저를 구할 수 있다.
getOrthonormaBasisMatrix(vector x, vector y) { x = normalize(x), y = normalize(y); y = y - dot(x, y) * x; z = cross(x,y) return matrix3(x, y, z) }
이 코드는 좌표계를 고려하지 않고, 작성한 것이기 때문에, 그 상황에서 쓸 좌표계, 벡터의 정확성, 행렬 구성 등을 고려해서 다시 짜야할것이다.
나는 위의 코드에서 일반 x,y,z축을 고려했고, 오른손 좌표계를 사용했다. 행렬 구성은 Column중심이여서, 각 벡터가 각 열에 들어가게 된다.
Chapter 3 The Laws of Motion
나는 위의 코드에서 일반 x,y,z축을 고려했고, 오른손 좌표계를 사용했다. 행렬 구성은 Column중심이여서, 각 벡터가 각 열에 들어가게 된다.
Chapter 3 The Laws of Motion
1. Point Mass == Particle
2. Particle은 Orientation이 없고(회전X), 이동하는 방향이(Velocity) 중요하다.
- Particle이 가지는 Property : Position, Velocity, Acceleration, damping, InverseMass
3. 뉴턴 1 : 만약 어떠한 force도 물체에 작용하지 않는다면, 한 오브젝트는 상수의 속도로(상수의 운동량(momentum)으로) 계속 움직인다.
4. 뉴턴 2: 한 오브젝트에 작용하는 한 force는 무체의 질량에 비례하는 가속도를 만들어낸다.
5. Simple form of drag == damping -> 오브젝트의 속도의 비율로 제거
- duration의 길이를 고려하지 않은 damping 식 (연산 cost가 싸서, 오브젝트가 많은 spark같은 것에 유용, 식은 나중의 integration을 알아야함).
- duration의 길이를 고려한 damping 식 (floating point의 지수승은 연산 cost가 비싸서, 오브젝트가 적당할 때 유용)
6.
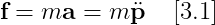
7.
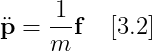
8. 운동량(Momentum) = Velocity * Mass
9. 만유인력의 법칙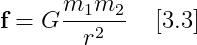
G : 만유인력 상수
r : 두 오브젝트 사이의 거리
m1을 지구의 오브젝트여서 상수로 가정,
r과 지구에 있는 오브젝트의 중심 사이의 거리는 이미 엄청 크고, 어디에 있든 크게 차이가 안나므로 상수로 가정,
이 가정을 통해 Simplification
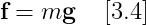
2. Particle은 Orientation이 없고(회전X), 이동하는 방향이(Velocity) 중요하다.
- Particle이 가지는 Property : Position, Velocity, Acceleration, damping, InverseMass
3. 뉴턴 1 : 만약 어떠한 force도 물체에 작용하지 않는다면, 한 오브젝트는 상수의 속도로(상수의 운동량(momentum)으로) 계속 움직인다.
4. 뉴턴 2: 한 오브젝트에 작용하는 한 force는 무체의 질량에 비례하는 가속도를 만들어낸다.
5. Simple form of drag == damping -> 오브젝트의 속도의 비율로 제거
- duration의 길이를 고려하지 않은 damping 식 (연산 cost가 싸서, 오브젝트가 많은 spark같은 것에 유용, 식은 나중의 integration을 알아야함).
- duration의 길이를 고려한 damping 식 (floating point의 지수승은 연산 cost가 비싸서, 오브젝트가 적당할 때 유용)
6.
7.
8. 운동량(Momentum) = Velocity * Mass
9. 만유인력의 법칙
G : 만유인력 상수
r : 두 오브젝트 사이의 거리
m1을 지구의 오브젝트여서 상수로 가정,
r과 지구에 있는 오브젝트의 중심 사이의 거리는 이미 엄청 크고, 어디에 있든 크게 차이가 안나므로 상수로 가정,
이 가정을 통해 Simplification
여기에서 g는 중력가속도가 된다. 이제 이 중력의 '힘'에 대한 Application
따라서, 중력의 힘은, 상수의 값으로 가속도에 그냥 넣어서 하는게 빠른 코드를 만들어낸다.
10. 적분 부분은 Chris Hecker Article 1로 더 자세히 설명.
Chris Hecker Article 1
1. Mechanics(역학)의 분류와 Rigid Body Dynamics
Mechanics(역학) : 물체에 작용하는 힘과 운동과의 관계에 대한 연구
- Dynamics(동역학) : 시간에 따른 운동량 변화를 일으키는 힘과 질량에 대한 연구
- Rigid Body Dynamics
- Kinematics(운동학) : 운동의 상태만을 연구. 물체의 위치, 속도, 가속도, 사이의 관계.
Rigid Body : 우리가 재현하려는 오브젝트(물체)에 부과하는 제약(모양이 변하지 않는다).
2. Calculus(미분적분학) : 위치, 속도, 가속도(Kinematic Quantities)가 시간에 따른 변화를 연구하는데 쓰이는 주된 Tool
미분적분한 -> 변화량에만 관계한다!
Analytic Integration : f(x)에 적분해서 일반식을 구한다.
Numerical Integration : 사칙연산으로 적분 값을 구한다 (Euler Method, Verlet Method..)
3. 미적분을 통한 위치, 속도, 가속도의 관계
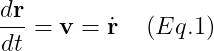r : 위치, v : 속도
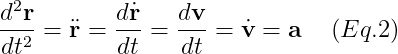a : 가속도
4. 1-Dimensional(1차원) Analytic Integration Example
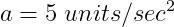
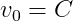
5. Dynamics에서 주된 두 가지 Quantities와 Force
- 두 가지 Quantities : Force, Mass
- Linear Momentum(선형 운동량) :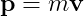
- Force Derivative
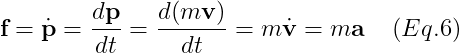
6. Rigid Body and Center of Mass about Force
부제 : 모든 point masses를 단일 point mass와(CM) 단일 velocity로 다루는 방법 유도.
- Rigid Body == A set of Point Masses (Particle)
위의 가정에 의해, 그 body를 구성하는 모든 points들의 운동량의 합은 Total Movement가 될 것이다. 즉,
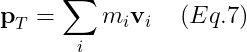m_i, v_i는 각 point masses의 번호
- Simplification with the Center of Mass
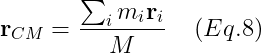M은 body의 total mass
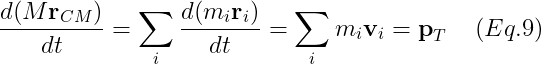
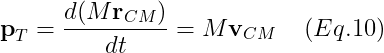
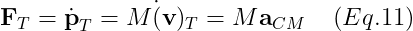
7. Analytic Integration VS Numerical integration
부제 : Numerical Integration of Ordinary Differential Equations(ODE)
- Differential Equations : 종속변수(y)의 도함수(y')가 종속변수(y) 그 자체와 독립변수 (x)외에도 방정식에 나타나는 방정식.
ex1) f(종속 변수) = 2t (독립 변수)
ex2) 공기마찰력 : 비행기가 빨리갈수록, 더 많은 공기 마찰이 생긴다. 즉,
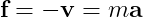
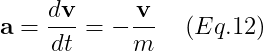Eq.12이 Ordinary Differential Equations(ODE).
즉,
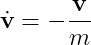
- The problem of ODE : 즉, a를 적분해서 v를 찾아야 하는데 v가 이미 식에 있는데 어떻게 찾는가?
- 대부분의 물리현상에 대한 방정식이 이러한 ODE 형태에 있기 때문에, ODE에 대한 연구가 많이 되었다.
- ODE 문제에 대한 해법은 'Numerical' Integration이다. 그 중 대표적인게 Euler Method.
- 용어가 어렵지만, 그 해법에 대해서 예를들어 간단히 말하자면,
2차원 곡선 y = x^2이 있다고 가정했을 때, x축이 t(time)이라하면,
각 x마다(time step만큼) slope를 찾는 것이다. 즉,
기울기를(변화율) 찾고 -> 그 변화율에 시간이 진행한 만큼 원래 값에 더해주면 적분이 되는 것이다. 식으로 표현하면
여기서 h는 time step의 시간이고, y_n에서의 변화율과 곱해서 y_n+1을 구하게된다.
공기마찰의 예제에 대해서
따라서,
8. 마무리
결론적으로 Chris Hecker의 자료에 따라서, 위치, 속도, 가속도의 관계를 알아냈고, Force는 선형운동량의 변화율인데, 이 선형 운동량이 질량과 속도의 곱이기 때문에, F = ma이라는 공식을 유도했다. 그리고, Rigid Body를 가기 위해 CM을 이용해 방정식의 Simplification을 유도했다. 그리고 움직임을 표현하기 위해 Integration 방식에 대해 설명하였고, 대표적인 Euler Numerical Integration Method를 설명했다. 결과적으로 이 이론과 GPED의 구현 팁에 의해서 코드는 :
An Introduction to Physically Based Modeling : Differential Equation Basics
(이건 그냥 번역함, 나도 처음 읽는 것이기 때문에)
1 초기값 문제(Initial Value Problems)
미분방정식은 unknown 함수와 그것의 도함수 사이의 관계를 설명한다. 미분방정식을 solve한다는 것은 일반적으로 어떤 부가적인 조건을 또한 만족하면서, 그 관계를 만족시키는 한 함수를 발견하는 것이다. 이 course에서, 우리는 우선적으로 특별한 계층의 문제와 관련될 것이다, initial value problems라고 불려지는. 고전적으로 여겨지는 초기값 문제에서, 그 system의 행동은 다음의 형태의 ordinary differential equation (ODE)로 묘사 된다
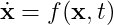
여기에서 f는 known function이고 (즉, 우리가 x와 t가 주어지면 측정할 수 있는 어떤 것), x는 그 system의 state(보통 함수에서의 y값), 그리고 dot(x)는 x의 시간에 대한 도함수이다. 일반적으로 x와 dot(x)는 벡터이다. 이름이 암시하듯이, 초기값 문제에서, 우리는 어떤 시작 시간 t0에서의 x(t0) = x0이 주어지고, 그 이후에 시간이 지남에 따라 x를 따르기를 원한다.
generic한 초기값 문제는 시각화하기에 쉽다. 2D에서, x(t)는 평면에서 점 p의 움직임을 묘사하는 한 curve를 만들어낸다. 어떤 점 x에서 그 함수 f는 2-vector를 제공하도록 측정되어질 수 있고, 그래서 s는 평면에서의 vector field를 정의한다 (see figure 1.) x에서 그 벡터는 움직이는 점 p가 가져야 하는 velocity이다, 만약 그것이 x를 관통해서 지나간다면 (그것이 그렇든 아니든.) f가 바다의 해류처럼 점에서 점으로 p를 움직이는 것으로 생각해라. p가 움직여지는 장소는 우리가 초기에 그것을 어디에 떨어 뜨리는지에 의존하지만, 일단 떨어지기만 한다면, 모든 미래의 움직임은 f에 의해 결정된다. f를 통해서 p에 의해 그려지는 궤도는 vector field의 integral curve를 형성한다. 그림 2를 보아라.
우리는 f를 x와 t의 함수로서 썼다. 그러나, 그 도함수는 시간에 직접적으로 의존할수도 안할 수도 있다. 만약 그것이 의존한다면, 그 점 p뿐만 아니라 그 vector field 그 자체도 움직인다, p의 속도가 그것이 어디에 있는지 뿐만 아니라 그것이 거기에 언제 도착하는지에도 의존하도록 하기 위해서이다. 그 경우에, 도함수 dot(x)는 두 가지 방식으로 시간을 의존한다: 첫 째로, 그 도함수 벡터들은 그 자체로 흔들거린다, 둘 째로, 그 점 p가 궤도 x(t) 위에서 움직이기 때문에, 그것은 다른 시간대에 다른 derivative vector들을 본다. 이 dual time dependence는 혼동되어서는 안된다. 만약 너가 물결모양의 벡터 필드를 통해 떠 다니는 한 파티클의 그림을 유지한다면.
2 Numerical Solutions
Standard introductory 미분 방정식은 symbolic solutions에 집중하는데, 거기에서 그 unknown function에 대해 함수 형태는 추측되어져야 한다. 예를들어, 그 미분 방정식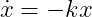
, 여기에서 dot(x)는 x의 시간 도함수를 나타낸다, 
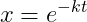에 의해 만족된다.
대조적으로, 우리는 numerical solutions에만 관계할 것이다, 거기에서, 우리는 initial value x(t0)으로 시작하는 discrete time steps을 이용한다. 한 단계 나아가기 위해, 우리는
time interval Δt에 대해 x의 대략적인 변화인 Δx를 계산하는 도함수 f를 사용한다. 그러고나서 그 새로운 값을 얻기 위해 Δx로 x를 증가시킨다. numerical solution에서 계산할 때, 그 도함수 f는 black box로서 간주된다 : 우리는 x와 t에 대해 numerical values를 제공하는데, dot(x)에 대한 numerical value를 결과로 받으면서. Numerical methods는 각 time step에서 한 개 또는 그 이상의 이러한 derivative evaluations를 수행하여 작동한다.
2.1 Euler's Method
그 가장 간단한 numerical method는 Euler's method라고 불려진다. x에 대한 우리의 초기값을 x0 = x(0)으로 표기하고, x의 우리의 estimate를 나중 시간 t0 + h에서 x(t0 + h)라고 표기하자. 여기에서 h는 stepsize 파라미터이다. 오일러 방법은 간단히 도함수 방향에서의 한 단계를 거쳐서 x(t0 + h)를 계산한다
너는 오일러 방법을 시각화하기 위해 2D vector field의 mental picture를 사용할 수 있따: 실제 integral curve 대신에, p는 polygonal path를 따르는데, 그것의 각 leg는 초기에 vector f를 evaluate해서 결정되고, h에 의해 스케일링 된다. 그림 3을 보아라.
간단할지라도, 오일러 방법은 정확하지 않다. integral curves가 중심이 같은 원들인 2D 함수 f의 경우를 고려하자. f에 의해 결정되는 한 점 p는 그것이 어떤 원에서 시작하든 영원히 궤도를 돌도록 예정되어 있다. 대신에, 각 오일러 스텝으로, p는 더 큰 반지름의 한 원에 직선으로 나아갈 것이다, 그것의 경로가 outward spiral를 따르도록 하면서. 그 stepsize를 줄이는 것은 이 outward drift의 비율을 느리게 할 것이지만, 결코 그것을 제거하지 못할 것이다.
게다가, 오일러 방법은 불안정할 수 있다. f = - kx의 1D 함수를 고려하자, 그것은 점 p가 기하급수적으로 0으로 되게끔 만들 것이다. 충분하게 작은 step sizes에 대해, 우리는 합리적은 행동을 얻을것이지만, h > 1/k일 때, 우리는 |Δx| > |x|를 가지고, 그래서 그 솔루션은 0에 대해서 oscillates 한다. h = 2/k를 넘어서, 그 oscillation은 발산하고, 그 시스템은 끝나버린다. 그림 4를 보아라.
마지막으로, 오일러 방법은 심지어 효율적이지 않다. 대부분의 numerical solution methods들은 거의 모든 그것들의 시간을 derivative evaluations를 수행하는데 쓴다, computational cost per step은 step당 evaluations의 횟수로 결정된다. 비록 오일러 방법이 step당 한 번의 evaluation을 요구할지라도, 한 방법의 실제 효율성은 그것이 너가 필요한 steps들의 사이즈에 의존한다 - 정확성과 안정성을 보존하면서 - 뿐만 아니라 step당 cost에도 의존한다. step당 4 또는 5번의 evaluations만큼을 요구하는 좀 더 정교한 methods들은 크게 오일러의 방법을 능가할 수 있다. 왜냐하면 그것들의 더 높은 cost per step은 그것들이 허용하는 더 큰 stepsizes에 의해 더 큰 offset이다.
오일러 방법에 대해 개선을 우리가 어떻게 하려는지를 이해하기 위해서, 우리는 그 방법이 만들어내는 에러를 좀 더 자세히 볼 필요가 있다. 무슨 일이 일어나는지를 이해하는 열쇠는 테일러 급수이다: x(t)가 smooth하다고 가정하여, 우리는 step의 끝에 그것의 값을 그 값과 초기에 도함수를 포함하는 무한한 합으로서 표현할 수 있다:
너가 볼 수 있듯이, 우리는 그 급수를 줄여서 Euler update formula를 얻는데, 우변의 처음에 두 항을 제외하고 모든 것을 다 버린다. 이것은 만약 첫 번째 이후의 모든 도함수가 0이라면 그 떄에만 옳다는 것을 의미한다, 즉 x(t)가 linear하다면 이다. Euler step과 full untruncated Taylor series 사이의 차이인 error term(항)은 leading term인
(h^2/2)ddot(x)(t0)에 의해 지배받는다. 결과적으로 우리는 그 에러를 O(h^2) (Order h squared라고 읽는다)라고 설명할 수 있다. 우리가 우리의 stepsize를 절반으로 자른다고 가정하자, 즉, 우리는 h/2 크기의 step을 가진다. 비록 이것이 우리가 h의 stepsize를 얻었을 때의 1/4의 에러만을 만들어 낼지라도, 우리는 어떤 주어진 interval에 대해 두 배의 steps을 가져야만 한다. 그것은 우리가 interval t0에서 t1에 대해 축적한 에러가 h에 대해 linear 하게 의존한다는 것을 의미한다. 이론적으로, 오일러 방법을 사용해서, 우리는 numerically하게 t0에서 t1으로 가는 interval에 대해 x를 계산 수 있다, 우리가 원한다면 거의 에러가 없이, 적절하게 작은 h를 선택하여. 실제로, 큰 많은 timesteps가 요구될지도 모른다, 에러와 함수 f에 의존하여.
2.2 The Midpoint Method
만약 우리가 ddot(x)뿐만 아니라 dot(x)를 evaluate할 수 있다면, 우리는 O(h^2) 대신에 truncated Taylor series에서 한 가지 추가 항을 유지하여 O(h^3) 정확도를 얻을 수 있다:
그 시간 미분 dot(x)가 f(x(t), t) 함수에 의해 주어진다는 것을 기억해라. 다음에 오는 것에서 간단함을 위해, 우리는 그 도함수 f가 x를 통해 간접적으로 시간에만 의존한다는 것을 가정할 것이다, dot(x) = f(x(t))가 되도록. 그 chain rule은 그러고나서 다음을 준다.
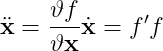
종종 복잡하고 expensive할 수 있는 f'를 evaluate해야만 하는 것을 피하기위해, 우리는 f의 관점에서 second-order term을 근사시킬 수 있고, 그 근사를 방정식 1로 대체하는데, 우리에게 O(h^3) error를 남긴다. 이것을 하기 위해서, 우리는 또 다른 Talyor expansion을 하고, f의 함수의 이 시간은
우리는 처음에 ddot(x)를 이 식으로 도입한다 다음을 선택해서
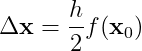
그리고 다음이 되게 하기 위해서이다
여기에서 x0 = x(t0)이다. 우리는 이제 양 변에 h (O(h^2) 항을 O(h^3)으로 바꾸려고)를 곱하고 다시 배치하면 다음을 만들어낸다
우변을 방정식 1로 바꾸는 것은 update formula를 준다.
이 공식은 처음에 Euler step을 evaluate하고, 그러고나서 그 step의 중간 점에서 second derivative evaluation을 수행한다. 그러므로 이름이 midpoint method이다. 그 midpoint method는 O(h^3) 내에서 올바르지만, f의 두 번의 evaluations을 요구한다. 그 method의 pictorial view를 위해 그림 5를 보아라.
우리는 O(h^3)의 에러에서 멈출 필요는 없다. f를 좀 더 많이 evaluate해서, 우리는 더 높은 차수의 derivatives를 제거할 수 있다. 이것을 하는 가장 인기 있는 procedure는 Runge-Kutta of order 4라고 불리는 방법이고, O(h^5)의 error per step을 가진다 (그 Midpoint method는 Runge-Kutta of order 2라고 불려진다.) 우리는 fourth order Runge-Kutta method를 유도하지 않을 것이지만, x(t0 + h)를 연산하는 그 공식은 아래에 기재되어있다
k1 = hf(x0, t0)
k2 = hf(x0 + k1/2, t0 + h/2)
k3 = hf(x0 + k2/2, t0 + h/2)
k4 = hf(x0 + k3, t0 + h)
x(t0 + h) = x0 + 1/6*k1 + 1/3 * k2 + 1/3 * k3 + 1/6 * k4
3 Adaptive Stepsizes
방법이 무엇이던간에, 중요한 문제는 좋은 stepsize를 결정하는데 놓여있다. 이상적으로, 우리는 h를 가능한 크게 선택하고 싶지만, 우리에게 비합리적은 에러를 줄만큼 크게는 아니고, 불안정성을 이끌어내는 만큼도 아니다. 만약 우리가 고정된 stepsize를 선택한다면, 우리는 오직 x(t)의 "worst" sections이 허용하는 만큼의 빠르게 진행할 수만 있따. 우리가 하고 싶은 것은 우리가 시간에서 앞으로 나아감에 따라 h를 변하게 하는 것이다. 우리가 h를 너무 많은 에러를 발생시키는 것없이 크게 만들 때 마다, 우리는 그렇게 해야만 한다. h가 초과 에러를 피하기 위해 줄어들어야만 할 때, 우리는 또한 그것을 하길 원한다. 이것이 adaptive stepsizing의 아이디어이다: ODE를 해결하는 과정에서 h를 다르게 하는 것이다.
여기에서 우리는 Euler method에 대한 adaptive stepsizing을 보여줄 것이다. 기본 아이디어는 다음과 같다. 우리가 주어진 stepsize h를 가진다고 가정하고, 우리가 그것이 얼마나 많이 바껴야 하는지를 알길 원한다고 가정하자.
우리가 x(t0 + h)에 대해 두 개의 estimates를 연산한다고 가정하자, size h의 euler step을 취해 t0 에서 t0 + h까지의 estimate x_a를 연산한다. 우리는 또한 h/2 크기의 two Euler step을 취해서, t0에서 t0 + h까지의 estimate x_b를 연산한다. x_a와 x_b둘 다 x(t0 + h)의 실제 값과 O(h^2)정도로 다르다. 그것은 O(h^2)에 의해 x_a와 x_b가 서로 다르다는 것을 의미한다. 결과적으로, 우리는 현재 에러 e의 측정값은
e = |x_a - x_b|
라고 쓸 수 있다. 이것은 우리에게 Euler step size h를 취할 때 에러에 대해 편리한 측정치를 준다.
우리가 step당 10^-4만큼의 에러를 기꺼이 가질 것이라고 가정하고, 그 현재 에러가 10^-8이라고 하자. 그 에러는 h^2으로서 올라가기 때문에, 우리는 stepsize를 늘릴 수 있다 다음으로,
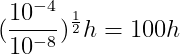
역으로, 만약 우리가 현재 10^-3의 에러를 가지고 있고, 10^-4의 에러까지 허용할 수 있따면, 우리는 그 stepsize를 줄여야만 한다.
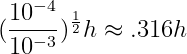
Adaptive stepsizing은 매우 추천되는 기법이다.
4 Implementation
우리가 해결하고 싶을 그 ODE들은 많은 것을 나타낼지도 모른다 - 예를들어, 질량과 스프링들의 조합, 어떤 rigid bodies, 또는 변형가능한 오브젝트. 우리는 ODE solvers와 그 model 구현하기를 원한다. 그 모델에서, 그것들은 다른것의 내부 세부사항으로부터 각각을 고립시큰 방식으로 작동한다. 이것은 solvers를 쉽게 바꾸는 것을 가능하게 하고, 그 solver code가 재사용가능하게 만들 것이다. 운 좋게도, 이러한 modularity의 종류는 달성하기에 어렵지 않다, 왜냐하면 모든 solvers가 작고 stereotyped된 연산들의 집합의 관점에서 표현되기 때문이다. 아마도, ODE에 관리되는 오브젝트들의 시스템은 어떤 종류의 구조에서 구체화 될 것이ㅏ. 그 접근법은 표준 연산들을 수행하기 위해 이 구조에 작동하는 type-specific code를 작성하는 것이고, 그러고나서 이러한 generic operations의 관점에서 solvers를 구현하는 것이다.
solver의 관점으로부터 그것이 작동하는 시스템은 블랙박스 함수 f(x,t)이다. 그 solver는 f를 evaluate할 수 있을 필요가 있다, 요구되어지듯이, 어떤 x와 t의 값에서, 그러고나서, 그 업데이트된 x와 t를 install 할 수 있어야 한다, 한 time step이 취해질 때. 이러한 연산들을 지원하기 위해서, 해결되어야 할 ODE를 나타내는 그 오브젝트는 solver로부터 이러한 요구들을 다룰 수 있어야 한다:
10. 적분 부분은 Chris Hecker Article 1로 더 자세히 설명.
Chris Hecker Article 1
1. Mechanics(역학)의 분류와 Rigid Body Dynamics
Mechanics(역학) : 물체에 작용하는 힘과 운동과의 관계에 대한 연구
- Dynamics(동역학) : 시간에 따른 운동량 변화를 일으키는 힘과 질량에 대한 연구
- Rigid Body Dynamics
- Kinematics(운동학) : 운동의 상태만을 연구. 물체의 위치, 속도, 가속도, 사이의 관계.
Rigid Body : 우리가 재현하려는 오브젝트(물체)에 부과하는 제약(모양이 변하지 않는다).
2. Calculus(미분적분학) : 위치, 속도, 가속도(Kinematic Quantities)가 시간에 따른 변화를 연구하는데 쓰이는 주된 Tool
미분적분한 -> 변화량에만 관계한다!
Analytic Integration : f(x)에 적분해서 일반식을 구한다.
Numerical Integration : 사칙연산으로 적분 값을 구한다 (Euler Method, Verlet Method..)
3. 미적분을 통한 위치, 속도, 가속도의 관계
4. 1-Dimensional(1차원) Analytic Integration Example
5. Dynamics에서 주된 두 가지 Quantities와 Force
- 두 가지 Quantities : Force, Mass
- Linear Momentum(선형 운동량) :
- Force Derivative
6. Rigid Body and Center of Mass about Force
부제 : 모든 point masses를 단일 point mass와(CM) 단일 velocity로 다루는 방법 유도.
- Rigid Body == A set of Point Masses (Particle)
위의 가정에 의해, 그 body를 구성하는 모든 points들의 운동량의 합은 Total Movement가 될 것이다. 즉,
- Simplification with the Center of Mass
7. Analytic Integration VS Numerical integration
부제 : Numerical Integration of Ordinary Differential Equations(ODE)
- Differential Equations : 종속변수(y)의 도함수(y')가 종속변수(y) 그 자체와 독립변수 (x)외에도 방정식에 나타나는 방정식.
ex1) f(종속 변수) = 2t (독립 변수)
ex2) 공기마찰력 : 비행기가 빨리갈수록, 더 많은 공기 마찰이 생긴다. 즉,
즉,
- The problem of ODE : 즉, a를 적분해서 v를 찾아야 하는데 v가 이미 식에 있는데 어떻게 찾는가?
- 대부분의 물리현상에 대한 방정식이 이러한 ODE 형태에 있기 때문에, ODE에 대한 연구가 많이 되었다.
- ODE 문제에 대한 해법은 'Numerical' Integration이다. 그 중 대표적인게 Euler Method.
- 용어가 어렵지만, 그 해법에 대해서 예를들어 간단히 말하자면,
2차원 곡선 y = x^2이 있다고 가정했을 때, x축이 t(time)이라하면,
각 x마다(time step만큼) slope를 찾는 것이다. 즉,
기울기를(변화율) 찾고 -> 그 변화율에 시간이 진행한 만큼 원래 값에 더해주면 적분이 되는 것이다. 식으로 표현하면
공기마찰의 예제에 대해서
따라서,
8. 마무리
결론적으로 Chris Hecker의 자료에 따라서, 위치, 속도, 가속도의 관계를 알아냈고, Force는 선형운동량의 변화율인데, 이 선형 운동량이 질량과 속도의 곱이기 때문에, F = ma이라는 공식을 유도했다. 그리고, Rigid Body를 가기 위해 CM을 이용해 방정식의 Simplification을 유도했다. 그리고 움직임을 표현하기 위해 Integration 방식에 대해 설명하였고, 대표적인 Euler Numerical Integration Method를 설명했다. 결과적으로 이 이론과 GPED의 구현 팁에 의해서 코드는 :
void GPEDParticle::integrate(real duration) { assert(duration > 0.0); // Update linear position m_position += m_velocity * duration; // Work out the acceleration from the force glm::vec3 resultingAcc = m_acceleration; resultingAcc += m_forceAccum * inverseMass; // Update linear velocity from the acceleration m_velocity += resultingAcc * duration; // Impose drag m_velocity *= real_pow(damping, duration); clearAccumulator(); }
An Introduction to Physically Based Modeling : Differential Equation Basics
(이건 그냥 번역함, 나도 처음 읽는 것이기 때문에)
1 초기값 문제(Initial Value Problems)
미분방정식은 unknown 함수와 그것의 도함수 사이의 관계를 설명한다. 미분방정식을 solve한다는 것은 일반적으로 어떤 부가적인 조건을 또한 만족하면서, 그 관계를 만족시키는 한 함수를 발견하는 것이다. 이 course에서, 우리는 우선적으로 특별한 계층의 문제와 관련될 것이다, initial value problems라고 불려지는. 고전적으로 여겨지는 초기값 문제에서, 그 system의 행동은 다음의 형태의 ordinary differential equation (ODE)로 묘사 된다
여기에서 f는 known function이고 (즉, 우리가 x와 t가 주어지면 측정할 수 있는 어떤 것), x는 그 system의 state(보통 함수에서의 y값), 그리고 dot(x)는 x의 시간에 대한 도함수이다. 일반적으로 x와 dot(x)는 벡터이다. 이름이 암시하듯이, 초기값 문제에서, 우리는 어떤 시작 시간 t0에서의 x(t0) = x0이 주어지고, 그 이후에 시간이 지남에 따라 x를 따르기를 원한다.
generic한 초기값 문제는 시각화하기에 쉽다. 2D에서, x(t)는 평면에서 점 p의 움직임을 묘사하는 한 curve를 만들어낸다. 어떤 점 x에서 그 함수 f는 2-vector를 제공하도록 측정되어질 수 있고, 그래서 s는 평면에서의 vector field를 정의한다 (see figure 1.) x에서 그 벡터는 움직이는 점 p가 가져야 하는 velocity이다, 만약 그것이 x를 관통해서 지나간다면 (그것이 그렇든 아니든.) f가 바다의 해류처럼 점에서 점으로 p를 움직이는 것으로 생각해라. p가 움직여지는 장소는 우리가 초기에 그것을 어디에 떨어 뜨리는지에 의존하지만, 일단 떨어지기만 한다면, 모든 미래의 움직임은 f에 의해 결정된다. f를 통해서 p에 의해 그려지는 궤도는 vector field의 integral curve를 형성한다. 그림 2를 보아라.
우리는 f를 x와 t의 함수로서 썼다. 그러나, 그 도함수는 시간에 직접적으로 의존할수도 안할 수도 있다. 만약 그것이 의존한다면, 그 점 p뿐만 아니라 그 vector field 그 자체도 움직인다, p의 속도가 그것이 어디에 있는지 뿐만 아니라 그것이 거기에 언제 도착하는지에도 의존하도록 하기 위해서이다. 그 경우에, 도함수 dot(x)는 두 가지 방식으로 시간을 의존한다: 첫 째로, 그 도함수 벡터들은 그 자체로 흔들거린다, 둘 째로, 그 점 p가 궤도 x(t) 위에서 움직이기 때문에, 그것은 다른 시간대에 다른 derivative vector들을 본다. 이 dual time dependence는 혼동되어서는 안된다. 만약 너가 물결모양의 벡터 필드를 통해 떠 다니는 한 파티클의 그림을 유지한다면.
2 Numerical Solutions
Standard introductory 미분 방정식은 symbolic solutions에 집중하는데, 거기에서 그 unknown function에 대해 함수 형태는 추측되어져야 한다. 예를들어, 그 미분 방정식
대조적으로, 우리는 numerical solutions에만 관계할 것이다, 거기에서, 우리는 initial value x(t0)으로 시작하는 discrete time steps을 이용한다. 한 단계 나아가기 위해, 우리는
time interval Δt에 대해 x의 대략적인 변화인 Δx를 계산하는 도함수 f를 사용한다. 그러고나서 그 새로운 값을 얻기 위해 Δx로 x를 증가시킨다. numerical solution에서 계산할 때, 그 도함수 f는 black box로서 간주된다 : 우리는 x와 t에 대해 numerical values를 제공하는데, dot(x)에 대한 numerical value를 결과로 받으면서. Numerical methods는 각 time step에서 한 개 또는 그 이상의 이러한 derivative evaluations를 수행하여 작동한다.
2.1 Euler's Method
그 가장 간단한 numerical method는 Euler's method라고 불려진다. x에 대한 우리의 초기값을 x0 = x(0)으로 표기하고, x의 우리의 estimate를 나중 시간 t0 + h에서 x(t0 + h)라고 표기하자. 여기에서 h는 stepsize 파라미터이다. 오일러 방법은 간단히 도함수 방향에서의 한 단계를 거쳐서 x(t0 + h)를 계산한다
너는 오일러 방법을 시각화하기 위해 2D vector field의 mental picture를 사용할 수 있따: 실제 integral curve 대신에, p는 polygonal path를 따르는데, 그것의 각 leg는 초기에 vector f를 evaluate해서 결정되고, h에 의해 스케일링 된다. 그림 3을 보아라.
간단할지라도, 오일러 방법은 정확하지 않다. integral curves가 중심이 같은 원들인 2D 함수 f의 경우를 고려하자. f에 의해 결정되는 한 점 p는 그것이 어떤 원에서 시작하든 영원히 궤도를 돌도록 예정되어 있다. 대신에, 각 오일러 스텝으로, p는 더 큰 반지름의 한 원에 직선으로 나아갈 것이다, 그것의 경로가 outward spiral를 따르도록 하면서. 그 stepsize를 줄이는 것은 이 outward drift의 비율을 느리게 할 것이지만, 결코 그것을 제거하지 못할 것이다.
게다가, 오일러 방법은 불안정할 수 있다. f = - kx의 1D 함수를 고려하자, 그것은 점 p가 기하급수적으로 0으로 되게끔 만들 것이다. 충분하게 작은 step sizes에 대해, 우리는 합리적은 행동을 얻을것이지만, h > 1/k일 때, 우리는 |Δx| > |x|를 가지고, 그래서 그 솔루션은 0에 대해서 oscillates 한다. h = 2/k를 넘어서, 그 oscillation은 발산하고, 그 시스템은 끝나버린다. 그림 4를 보아라.
마지막으로, 오일러 방법은 심지어 효율적이지 않다. 대부분의 numerical solution methods들은 거의 모든 그것들의 시간을 derivative evaluations를 수행하는데 쓴다, computational cost per step은 step당 evaluations의 횟수로 결정된다. 비록 오일러 방법이 step당 한 번의 evaluation을 요구할지라도, 한 방법의 실제 효율성은 그것이 너가 필요한 steps들의 사이즈에 의존한다 - 정확성과 안정성을 보존하면서 - 뿐만 아니라 step당 cost에도 의존한다. step당 4 또는 5번의 evaluations만큼을 요구하는 좀 더 정교한 methods들은 크게 오일러의 방법을 능가할 수 있다. 왜냐하면 그것들의 더 높은 cost per step은 그것들이 허용하는 더 큰 stepsizes에 의해 더 큰 offset이다.
오일러 방법에 대해 개선을 우리가 어떻게 하려는지를 이해하기 위해서, 우리는 그 방법이 만들어내는 에러를 좀 더 자세히 볼 필요가 있다. 무슨 일이 일어나는지를 이해하는 열쇠는 테일러 급수이다: x(t)가 smooth하다고 가정하여, 우리는 step의 끝에 그것의 값을 그 값과 초기에 도함수를 포함하는 무한한 합으로서 표현할 수 있다:
너가 볼 수 있듯이, 우리는 그 급수를 줄여서 Euler update formula를 얻는데, 우변의 처음에 두 항을 제외하고 모든 것을 다 버린다. 이것은 만약 첫 번째 이후의 모든 도함수가 0이라면 그 떄에만 옳다는 것을 의미한다, 즉 x(t)가 linear하다면 이다. Euler step과 full untruncated Taylor series 사이의 차이인 error term(항)은 leading term인
(h^2/2)ddot(x)(t0)에 의해 지배받는다. 결과적으로 우리는 그 에러를 O(h^2) (Order h squared라고 읽는다)라고 설명할 수 있다. 우리가 우리의 stepsize를 절반으로 자른다고 가정하자, 즉, 우리는 h/2 크기의 step을 가진다. 비록 이것이 우리가 h의 stepsize를 얻었을 때의 1/4의 에러만을 만들어 낼지라도, 우리는 어떤 주어진 interval에 대해 두 배의 steps을 가져야만 한다. 그것은 우리가 interval t0에서 t1에 대해 축적한 에러가 h에 대해 linear 하게 의존한다는 것을 의미한다. 이론적으로, 오일러 방법을 사용해서, 우리는 numerically하게 t0에서 t1으로 가는 interval에 대해 x를 계산 수 있다, 우리가 원한다면 거의 에러가 없이, 적절하게 작은 h를 선택하여. 실제로, 큰 많은 timesteps가 요구될지도 모른다, 에러와 함수 f에 의존하여.
2.2 The Midpoint Method
만약 우리가 ddot(x)뿐만 아니라 dot(x)를 evaluate할 수 있다면, 우리는 O(h^2) 대신에 truncated Taylor series에서 한 가지 추가 항을 유지하여 O(h^3) 정확도를 얻을 수 있다:
그 시간 미분 dot(x)가 f(x(t), t) 함수에 의해 주어진다는 것을 기억해라. 다음에 오는 것에서 간단함을 위해, 우리는 그 도함수 f가 x를 통해 간접적으로 시간에만 의존한다는 것을 가정할 것이다, dot(x) = f(x(t))가 되도록. 그 chain rule은 그러고나서 다음을 준다.
종종 복잡하고 expensive할 수 있는 f'를 evaluate해야만 하는 것을 피하기위해, 우리는 f의 관점에서 second-order term을 근사시킬 수 있고, 그 근사를 방정식 1로 대체하는데, 우리에게 O(h^3) error를 남긴다. 이것을 하기 위해서, 우리는 또 다른 Talyor expansion을 하고, f의 함수의 이 시간은
우리는 처음에 ddot(x)를 이 식으로 도입한다 다음을 선택해서
그리고 다음이 되게 하기 위해서이다
여기에서 x0 = x(t0)이다. 우리는 이제 양 변에 h (O(h^2) 항을 O(h^3)으로 바꾸려고)를 곱하고 다시 배치하면 다음을 만들어낸다
우변을 방정식 1로 바꾸는 것은 update formula를 준다.
이 공식은 처음에 Euler step을 evaluate하고, 그러고나서 그 step의 중간 점에서 second derivative evaluation을 수행한다. 그러므로 이름이 midpoint method이다. 그 midpoint method는 O(h^3) 내에서 올바르지만, f의 두 번의 evaluations을 요구한다. 그 method의 pictorial view를 위해 그림 5를 보아라.
우리는 O(h^3)의 에러에서 멈출 필요는 없다. f를 좀 더 많이 evaluate해서, 우리는 더 높은 차수의 derivatives를 제거할 수 있다. 이것을 하는 가장 인기 있는 procedure는 Runge-Kutta of order 4라고 불리는 방법이고, O(h^5)의 error per step을 가진다 (그 Midpoint method는 Runge-Kutta of order 2라고 불려진다.) 우리는 fourth order Runge-Kutta method를 유도하지 않을 것이지만, x(t0 + h)를 연산하는 그 공식은 아래에 기재되어있다
k1 = hf(x0, t0)
k2 = hf(x0 + k1/2, t0 + h/2)
k3 = hf(x0 + k2/2, t0 + h/2)
k4 = hf(x0 + k3, t0 + h)
x(t0 + h) = x0 + 1/6*k1 + 1/3 * k2 + 1/3 * k3 + 1/6 * k4
3 Adaptive Stepsizes
방법이 무엇이던간에, 중요한 문제는 좋은 stepsize를 결정하는데 놓여있다. 이상적으로, 우리는 h를 가능한 크게 선택하고 싶지만, 우리에게 비합리적은 에러를 줄만큼 크게는 아니고, 불안정성을 이끌어내는 만큼도 아니다. 만약 우리가 고정된 stepsize를 선택한다면, 우리는 오직 x(t)의 "worst" sections이 허용하는 만큼의 빠르게 진행할 수만 있따. 우리가 하고 싶은 것은 우리가 시간에서 앞으로 나아감에 따라 h를 변하게 하는 것이다. 우리가 h를 너무 많은 에러를 발생시키는 것없이 크게 만들 때 마다, 우리는 그렇게 해야만 한다. h가 초과 에러를 피하기 위해 줄어들어야만 할 때, 우리는 또한 그것을 하길 원한다. 이것이 adaptive stepsizing의 아이디어이다: ODE를 해결하는 과정에서 h를 다르게 하는 것이다.
여기에서 우리는 Euler method에 대한 adaptive stepsizing을 보여줄 것이다. 기본 아이디어는 다음과 같다. 우리가 주어진 stepsize h를 가진다고 가정하고, 우리가 그것이 얼마나 많이 바껴야 하는지를 알길 원한다고 가정하자.
우리가 x(t0 + h)에 대해 두 개의 estimates를 연산한다고 가정하자, size h의 euler step을 취해 t0 에서 t0 + h까지의 estimate x_a를 연산한다. 우리는 또한 h/2 크기의 two Euler step을 취해서, t0에서 t0 + h까지의 estimate x_b를 연산한다. x_a와 x_b둘 다 x(t0 + h)의 실제 값과 O(h^2)정도로 다르다. 그것은 O(h^2)에 의해 x_a와 x_b가 서로 다르다는 것을 의미한다. 결과적으로, 우리는 현재 에러 e의 측정값은
e = |x_a - x_b|
라고 쓸 수 있다. 이것은 우리에게 Euler step size h를 취할 때 에러에 대해 편리한 측정치를 준다.
우리가 step당 10^-4만큼의 에러를 기꺼이 가질 것이라고 가정하고, 그 현재 에러가 10^-8이라고 하자. 그 에러는 h^2으로서 올라가기 때문에, 우리는 stepsize를 늘릴 수 있다 다음으로,
역으로, 만약 우리가 현재 10^-3의 에러를 가지고 있고, 10^-4의 에러까지 허용할 수 있따면, 우리는 그 stepsize를 줄여야만 한다.
Adaptive stepsizing은 매우 추천되는 기법이다.
4 Implementation
우리가 해결하고 싶을 그 ODE들은 많은 것을 나타낼지도 모른다 - 예를들어, 질량과 스프링들의 조합, 어떤 rigid bodies, 또는 변형가능한 오브젝트. 우리는 ODE solvers와 그 model 구현하기를 원한다. 그 모델에서, 그것들은 다른것의 내부 세부사항으로부터 각각을 고립시큰 방식으로 작동한다. 이것은 solvers를 쉽게 바꾸는 것을 가능하게 하고, 그 solver code가 재사용가능하게 만들 것이다. 운 좋게도, 이러한 modularity의 종류는 달성하기에 어렵지 않다, 왜냐하면 모든 solvers가 작고 stereotyped된 연산들의 집합의 관점에서 표현되기 때문이다. 아마도, ODE에 관리되는 오브젝트들의 시스템은 어떤 종류의 구조에서 구체화 될 것이ㅏ. 그 접근법은 표준 연산들을 수행하기 위해 이 구조에 작동하는 type-specific code를 작성하는 것이고, 그러고나서 이러한 generic operations의 관점에서 solvers를 구현하는 것이다.
solver의 관점으로부터 그것이 작동하는 시스템은 블랙박스 함수 f(x,t)이다. 그 solver는 f를 evaluate할 수 있을 필요가 있다, 요구되어지듯이, 어떤 x와 t의 값에서, 그러고나서, 그 업데이트된 x와 t를 install 할 수 있어야 한다, 한 time step이 취해질 때. 이러한 연산들을 지원하기 위해서, 해결되어야 할 ODE를 나타내는 그 오브젝트는 solver로부터 이러한 요구들을 다룰 수 있어야 한다:
- dim(x)를 반환해라. x와 dot(x)가 vectors이기 때문에, 그 solver는 그것들의 length를 알아야 한다, storage를 할당하고, vector arithmetic operations 등을 하기 위해서.
- Get/set x and t. 그 solver는 한 step의 끝에서 새로운 값을 install할 수 있어야만 한다. 게다가, multi-step method는 x와 t를 중간값으로 설정해야만 한다, derivative evaulations을 수행하는 도중에.
- 현재 x와 t에서 f를 evaluate해라.
객체지향언어에서, 이러한 연산들은 자연적으로 type-specific way로 다뤄지는 generic functions 구현될 것이다. 객체지향이 아닌 언어에서, generic functions들은 structure slots에서 type-specific functions에 대한 포인터들을 install하여 faked될 것이고, 또는 간단히 solver에 인자로서 함수 포인터들을 넘길 것이다. 나주엥, 우리는 이러한 연산들이 어떻게 particle-and-spring systems같은 특정한 모델들에 대해 구현되어야 할지를 상세히 고려할 것이다.
댓글 없음:
댓글 쓰기