내가 모르는 것과, 익숙치 않은 것들 위주로 정리.
Chapter 3 A Math and Geometry Primer
충돌 탐지는 매우 기하학적인 특성의 분야이다. 예를들어, world simulation에서,그 월드의 world와 오브젝트들 둘 다 폴리곤, 구, 박스같은 geometrical entities로 표현된다. 이러한 entities에 대한 효율적인 intersection tests를 구현하기 위해서, 벡터, 행렬, 선형대수에 대해 일반적으로 철저한 이해가 요구된다. 비록 이 책이 독자가 이러한 주제들에 대해 어느정도 경험이 있다고 가정할지라도, 이 챕터에서 그 범위는 편의성을 위해 제공된다. 이것은 책 도처에서 관련된 개념, 정의 그리고 항등식으로서 역할을 한다. 그 보여주는 것은 informal review로서 의도되었다, 철저한 formal treatment라기 보다는. vector space에 대해 좀 더 공식적이고 encompassing converage, 선형대수와 기하에 관심이 있는 독자들은 [Hausner98] or [Anton00]과 같은 교재들을 찾아보길 원할지도 모른다.
이 챕터는 또한 computational geometry로부터의 몇 가지 개념을 보여준다 (예를들어, Voronoi regions and convex hulls) 그리고 convex sets의 이론(볼록 집합의 이론)으로 부터 (separating planes, support mappings, and Minkowski sums and differences). 이러한 개념들은 이 책에서 나타나는 많은 알고리즘에 중요하다.
3.1 Matrices
행렬 기본
3.1.1 행렬 연산
3.1.2 행렬과 관련된 대수 항등식
3.1.3 determinants(행렬식)
3.1.4 Cramer's Rule을 사용하여 선형 연립 방정식 풀기
3.1.5 역행렬
3.1.6 Determinant Predicates
행렬식은 또한 간결하게 geometrical tests를 표현하는데 유용하다. 가장은 아니더라도, 많은 geometrical tests는 행렬식의 형태로 바뀔 수 있다. 만야 한 행렬식이 robustly하고 효율적으로 얻어질 수 있다면, geometrical test도 그럴 수 있다. 그러므로, 행렬식의 평가는 잘 연구되어져야 한다. 특히, 한 행렬식의 기호는 많은 geometrical tests에서 중요한 역할을한다. 그리고 종종 orientation, sidedness, inclusion of points를 테스트하는 topological predicates로서 사용된다. determinant predicates의 직접적인 evaluation은 (예를들어, 어떤 공통된 subexpression elimination을 적용하는 것 없이), 일반적으로 가장 효율적이고 또는 튼튼한식을 만들지 않는 다는 것에 주목해라. 또한 부동소수점 연산을 사용한 determinant predicates가 rounding errors에 매우 민감하고, degenerate configurations에서 올바른 sign에 의존하는 알고리즘들은 의도되로 작동하지 않을 가능성이 높다. robustness에서 에러들과 그것들에 처리하는 것에 대해, Chapters 11과 12를 보아라. 그 caveat과 함께, determinants 프로그램으로서, 다음의 몇 가지 섹션들은 이러한 topological predicates의 몇 가지 유용한 것들을 보여준다.
3.1.6.1 ORIENT2D(A,B,C)
A = (a_x, a_y), B = (b_x, b_Y), C = (c_x, c_y)인 세 개의 2D 점이라고 하자, 그리고 ORIENT2D(A,B,C)는 다음으로 정의 된다
{
행렬식에서 Row Replacement를(행 대치) 쓰게 된다면, 행렬식의 값은 바뀌지 않는다 따라서, 3행에 -1을 곱한 것을 1행과 2행에 더해주고, 여인수를 통해 행렬식을 바꿔준다면
마지막의 식이 나온다.
}
만약 ORIENT2D(A,B,C) > 0이라면, C는 directed line AB의 왼쪽에 놓여있다. 같은 말로, 삼각형 ABC는 반시계 방향이다. ORIENT2D(A,B,C) < 0일 때, C는 directed line AB의 오른쪽에 있고, 삼각형 ABC는 시계 방향이다. ORIENT2D(A,B,C) = 0일 때, 그 세 개의 점은 일직선에 있따. ORIENT2D(A,B,C)에 의해 반환된 실제 값은 삼각형 ABD의 양의 넓이의 두 배와 일치한다 (ABC가 시계 반대방향이면 양수이고, 그렇지 않다면 음수이다). 대안적으로, 이 행렬식은 점 A = (a_x, a_y)와 B = (b_x, b_y)를 통과하는 2D line L(x,y) = 0의 implicit equation으로 보일 수 있다. L(x,y)를 다음으로 정의해서
{
이것에 대한 직관적 이해는, 오른손 법칙을 설명한 http://degurii.tistory.com/47 이 링크로도 이해할 수 있으나, 내가 생각해낸 이해로도 알 수 있다. 이건 이 식을 통해 알아낸 것인데, 자신이 직접 그림을 그리면서 해보면 알 수 있다.
상황을 간단하게 하기 위해 이차원 x축 y축 상에 C를 원점으로 두어라. 시계방향인지 반시계 방향인지를 판단하기 위해 반드시 A->B->C의 정점 순서대로 가도록 해라.
이 책에서 나온 저 식의 행렬식을 최종적으로 계산해보면
이렇게 되는데, 사실 이것은
이렇게 간단화 해보면
D를 이렇게 간단하게 볼 수 있다.
그러면 먼저 C를 원점으로 두고 시계 반대방향으로 A와 B를 점 찍어서 CA, CB 벡터를 그어보아라. 그리고 저 변환된 D가 무엇을 뜻하는지 볼 수 있다.
즉, CA의 x좌표와 CB의 y좌표가 만드는 직사각형의 넓이
CB의 x좌표와 CA의 Y좌표가 만드는 직사각형의 넓이 뺄셈이다.
그래서 이 직사각형의 넓이의 뺄셈은 ABC가 시계 반대방향일 때 항상 양수이고,
시계 방향일 때는 음수이고, ABC가 일직선일 때는 0이 된다.
확실히 이해하기 위해 시계 방향일 때와 일직선일 때 둘 다 케이스를 직접 그려보면 이해가 될 것이다. 즉 한 점을 고정시켜놓고, 나머지 두 점에 대해 벡터를 만들어서, 그 벡터의 원소로 직사각형을 만들면 그 넓이에 어떤 규칙성이 생긴다는 것을 알 수 있다.
쇼펜하우어가 말했듯이, 기하를 이렇게 직관적으로 이해하는 것은 매우 좋은 것이다.
}
3.1.6.2 ORIENT3D(A,B,C,D)
3D의 점들 A,B,C,D가 주어진다면, ORIENT3D(AB,C,D)를 다음으로 정의하자
ORIENT3D(A,B,C,D) < 0일 때, D는 삼각형 ABC의 supporting plane의 위에 놓여있고, D에서 보아질 때, ABC는 시계 반대 방향으로 나타난다라는 의미이다. ORIENT3D(A,B,C,D) > 0이라면, D는 대신에 ABC의 평면 아래에 놓여 있다. ORIENT3D(A,B,C,D) = 0일 때, 그 4개의 점들은 동일 평면상에 있다. ORIENT3D(A,B,C,D)에 의해 반환된 값은 4개의 점들로 형성된 4면체의 양의 부피에 6배와 동일하다. 대안적으로 그 행렬식은 점들 A,B,C를 통과하는 3D 평먼 P(x,y,z) = 0의 implicit equation으로 보아질 수 있다. P(x,y,z)를 다음으로 정의해서
3.1.6.3 INCIRCLE2D(A,B,C,D)
4개의 2D 점들 A,B,C,D가 주어진다면, INCIRCLE2D(A,B,C,D)를 다음으로 정의하자
{
첫 번째 행렬식에 대한 증명은, 원의 일반 방정식을 두고, 세 점과 미지의 점 (x,y)를 두 었을 때, 일반 방정식에 대입하여 식을 보면은, 행렬으로 나타낼 수 있고, 선형 연립 일차 방정식을 푸는 것이 나온다. 따라서, 그것의 역행렬이 있어야 하므로, 행렬식이 0이여야 한다. 그래서 첫 번째 행렬식은 이해할 수 있었다.
그러나 두 번째 행렬식이 어떻게 도출 된 건지 모르겠다. 내 생각에는 첫 번째 행렬식에서 4번째 행으로 Row Replacement를 해서, a^2_x - d^2_x + a^2_y - d^2-y 가 되어야 하는데 왜 빼기 제곱을 더한 건지 모르겠다..
밑의 INSPHERE(AB,C,D,E)도 마찬가지이다.
}
ORIENT2D(A,B,C) > 0으로 나타내어져서, 삼각형 ABR가 시계 반대방향으로 나타난다고 하자. 그러고나서, INCIRCLE2D(A,B,C,D) > 0일 때, D는 세 개의 점들 A,B, 그리고 C를 지나는 원 안에 놓여있다. 만약 대신에 INCIRCLE2D(A,B,C,D) < 0이라면, D는 원 밖에 놓여있다. INCIRCLE2D(A,B,C,D) = 0일 때, 그 4개의 점들은 cocircular이다. 만약 ORIENT2D(A,B,C) < 0이라면, 그 결과는 반대이다.
3.1.6.4 INSPHERE(A,B,C,D,E)
5개의 3D 점들 A,B,C,D,E가 주어졌다면, INSHPERE(A,B,C,D,E)를 다음으로 정의하자
4개의 점들 A, B, C와 D가 ORINET3D(A,B,C,D) > 0 으로 방향지어졌다고 하자. INSPHERE(A,B,C,D,E) > 0 일 때, E는 A,B,C,D를 지나는 구 안에 놓여있다. 만약 대신에 INSPHERE(A,B,C,D,E) < 0 일 때, E는 구의 밖에 있따. INSPHERE(A,B,C,D,E) = 0일 때, 5개의 점들은 cospherical이다.
3.2 Coordinate Systems and Points
한 점은 공간에서 한 position을 갖는다. 그것의 위치는 좌표계의 관점으로 묘사되는데, origin이라고 불려지는 reference point가 주어지고, 좌표 축도 주어진다. n차원 좌표계에서 점들은 실수 값 (x_1, x_2, ..., x_n)의 n-tuple로 명시된 것이다. n-tuple은 그 점의 좌표라고 불려진다. n-tuple로 묘사되는 그 점은 원점에서 시작하여 첫 번째 좌표축을 따라 x_! 단위 만큼 움직이고, 두 번째 좌표축을 따라 x_2단위만큼 움직이고, 모든 주어진 수에 따라 그렇게 하여서 도달되는 것이다. 그 원점은 모드 zero components (0,0,...,0)인 점이다. 좌표계는 부모 좌표계와 상대적으로 주어질지도 모른다. 거기에서 종속된 좌표계의 원점은 부모 좌표계의 어떤 점과도 일치할지 모른다.
카르테시안(or rectangular) 좌표계가 주요 관심사이다. 거기에서, 좌표축들은 서로에게 수직이다. 2D 공간에 대해, 두 개의 좌표 축들은 전통적으로 x축과 y축으로 표기된다. 3D 공간에서, 세 번째 축은 z축으로 불려진다.
좌표 공간은 좌표계가 명시할 수 있는 점들의 집합이다. 좌표계는 이 공간을 span한다고 말해진다. 한 공간을 spanning하는 좌표 축들의 한 집합을 그 공간에 대한 the frame of reference or basis라고 불려진다. 주어진 좌표 공간에 대해 무한히 많은 frames of reference가 있다.
이 책에서, 점들은 이탈리어 체로 대문자로 표기된다 (예를들어, P, Q, 그리고 R). 점들은 벡터와 매우 관련있고, 다음섹션에서 이야기 된다.
3.3 Vectors
생략..
3.3.1 Vector Arithmetic
두 벡터 u와 v의 합 w는 w = u + v인데 u와 v의 컴포넌트들을 pairwise로 더하여서 만들어진다.
기하학적으로, 벡터 합은 u의 끝에 v에 대해 화살을 놓는 것이다. 그리고 그것들의 합은 u의 시작에서 부터 v의 끝까지를 가리키는 arrowr로 정의된다. 그 벡터 합의 이 기하학적 시각은 종종 벡터 합의 parallelogram law(평행사변형 법칙)으로 언급된다. 왜냐하면 그 합계가 만들어내는 벡터가 두 개의 주어진 벡터들에 의해 형성된 평행사변형의 대각선과 일치하기 떄문이다. 그림 3.2에서 보이듯이.
벡터의 뺄셈인 w = u - v는 u와 v의 negation의 덧셈으로 정의된다; 즉, w = u + (-v). 벡터 v의 negation -v는 동일한 크기의 벡터이지만 반대 방향이다. 그 벡터의 각 컴포넌트를 negate하여 얻어진다.
....
3.3.2 Algebraic Identities Involving Vectors
3.3.3 The Dot Product
두 벡터 u와 v의 dot product(or scalar product)는 그것들이ㅡ 대응되는 벡터 컴포넌트들의 곱의 합으로 정의도고, u dot v로 표기된다.
그 내적이 벡터가 아닌 스칼라라는 것에 주목해라. 한 벡터와 그 자체의 내적은 그 벡터의 제곱된 길이이다.
u와 v사이의 가장 작은 각 theta가 다음의 방정식을 만족한다는 것을 보여주는 것이 가능하다
u dot v = ||u|| ||v|| cos\theta
따라서 theta는 다음으로 얻어질 수 있다
\theta = cos^-1(u dot v / ||u|| ||v||)
결과적으로, 두 개의 zero가 아닌 벡터에 대해, 내적은 \theta가 예각일 때는 양수, 둔각일 때는 음수이고, 그 벡터가 수직일 때는 0이다 (그림 3.4). 두 벡터 사이의 각이 예각, 둔각, 또는 직각인지를 구분할 수 있는 것은 내적의 꽤 유용한 특징이다. 이것은 다양한 기하학적 테스트에서 사용된다.
기하학적으로 내적은 v의 u에 대한 사영으로도 볼 수 있다. 이것은 ||u||의 단위에서 u를 따라서 v의 양의 거리 d를 반환한다:
이 사영은 그림 3.5a에 그려져있다. 벡터 u와 v가 주어진다면, v는 그러므로 u에 평행한 벡터 p와 u에 수직인 벡터 q로 분해될 수 있다. 즉 v = p + q 이다:
그림 3.5b는 v가 어떻게 p와 q로 분해되는지를 보여준다.
내적은 교환법칙이 성립하기 때문에, u의 v로의 사영으로 보아도 유효하다. 그리고 이것은 ||v|| 단위에서 v를 따라 u의 거리를 반환한다.
3.3.4 Algebraic Identities Involving Dot Products
스칼라 r과 s 그리고 벡터 u와 v가 주어진다면, 다음의 항등식은 내적에 대해 유효하다:
3.3.5 The Cross Product
두 개의 3D 벡터 u와 v의 cross product(or vector product)는 벡터 컴포넌트의 관점에서 다음으로 정의 된다
그 결과는 u와 v에 수직인 벡터이다. 그것의 크기는 u와 v의 길이와 그것들 사이의 가장 작은 각 θ의 sin 값의 곱과 같다. 즉,
여기에서 n은 u와 v의 평면에 수직인 단위 벡터이다. w = u X v 그 외적을 만들 때, w에 대한 두 가지 가능한 방향에 대한 한 선택이 있다. 여기에서, 전통적으로 w의 방향은 u와 v가 함게 있을 때, 그것이 오른손 좌표계를 형성하도록 선택된다. 오른손 봅칙은 오른손 좌표계가 어떻게 생겼는지를 기억하기 위한 연상기호이다. 그것은 만약 손가락이 u에서 v로 가도록 하여 w 벡터에 대해 오른손이 굽어진다면, w의 방향은 연장된 엄지의 방향과 일치하다는 것을 말한다.
u X v의 크기는 u와 v로 spanned된 평행사변형의 넓이와 같다. 즉, 밑변 ||u||이고, 높이가 ||v|sinθ 이다 (그림 3.6). 그 크기는 그 벡터가 수직일 때 가장 크다.
행렬식과 친숙한 사람ㄷ르은 외적을 pesudo-determinant로 기억하는 것이 더 쉽다는 것을 알지도 모른다:
여기에서 i,j,k는 그 좌표 축들과 평행한 단위 벡터들이다. 그 외적은 또한 (skew-symmetric)행렬과 벡터의 곱으로서 행렬 형태로 표현될 수 있다:
외적이 이전에 보여진 6번의 곱 대신에 실제로 오직 5번의 곱을 사용하여 연산될 수 있다는 것을 주목할만큼 흥미롭다. 그것을 다음으로 표현할 수 있다
여기에서
이 공식은 9개에서 (6개의 곱, 3개의 덧셈) 13개(5번의 곱, 8번의 덧셈)의 총 연산 개수로 증가시키기 때문에, 그러한 다시 작성한 것의 어떤 결국의 실제 성능의 이득은 하드웨어 의존적이다.
삼각형 ABC가 주어진다면, 그것의 변 중에서 두 개의 외적의 크기는 ABC의 넓이의 두 배와 같다. 임의의 서로 교차하지 않는 4개의 변의 ABCD에 대해, 두 개의 대각선의 외적의 크기 ||e||인 e = (C - A) X (D-B)는 ABCD의 넓이의 두 배와 같다. 그림 3.7에서 이 특성이 보여진다.
2차원에서 외적과 직접적으로 같은 것은 없다, 평먼에서 두 개의 벡터에 대해 수직인 세 번째 벡터는 평면과 2D space를 떠나야 하기 때문이다. 가장 가까운 2D 유사한 것은 2D pseudo cross product이고, 다음으로 정의된다,
여기에서 u^\perp = (-u2, u1)는 u에 시계 반대 방향으로의 수직인 벡터이다. u^\perp 항은 "u-perp"라고 읽어진다. 이 이유 때문에, pesudeo cross product는 가끔씩 perp-dot product라고 언급된다. 2D pseudo cross product는 스칼라인데, 외적의 크기와 유사한 이 값은 u와 v에 의해 결정되는 평행사변형의 양의 넓이와 일치한다. v가 u로부터 반시계 방향이라면 그것은 양수이고, 시계방향이라면 음수이고, 그렇지 않다면 0이다.
또 다시, (3D) 삼각형 ABC가 주어진다면, d = (B - A) X (C - A)는 외적의 각 컴포넌트는 2D pseudo cross product로 구성되었다는 것에 주목해라 (중간 컴포넌트가 negated된). 그러므로 d의 각 컴포넌트는 개별적으로 ABC의 yz, zx, xy 평면으로의 사영의 양의 넓이의 두 배를 갖는다. 단일의 외적 연산은 그러므로, 2D point-in-triangle test의 결과를 결정하는데 충분하고, 이것은 외적 연산이 직접적으로 하드웨어에서 지원된다면 유용할 수 있다.
{
yz에서만 보자면, 식이
이렇게 된다. 그렇다면
AB벡터와 AC벡터가 있었는데,
dot(AB벡터^\perp, AC벡터)인 것과 같은 식이다.
이 때, y축과 z축밖에 없어서 2D로 볼 수가 있게 된다.
그래서, perp dot product는, dot(u^\perp, v) = |u||v|sinθ와 같기 때문에, 평행사변형의 넓이가 되어서, 삼각형 ABC를 yz 평면에 사영했을 때, 그 삼각형 넓이의 두 배가 된다.
}
3.3.6 Algebraic Identities Involving Cross Products
스칼라 r과 s 그리고 벡터 u,v,w,x가 주어진다면, 다음의 외적 항등식은 유효하다:
{
위에서 4번째 식은 (u와 v의 수직인 벡터와 u 또는 v와 내적을 하면 수직이므로 0이다)
아래에서 2번째 식은 (u와 v의 평면에 있는 벡터이고)
아래에서 1번째 식은 (v와 w의 평면에 있는 벡터이다.
}
Largrange identity는 다양한 기하 테스트에 요구되는 연산들의 개수를 줄이는데 특히 유용하다. 그러한 줄이는 것의 몇 가지 예제는 Chapter 5에서 발견된다.
3.3.7 The Scalar Triple Product
dot((u X v), w) 식은 충분히 빈번하게 발생하는데, 그래서 그것은 그것 자신의 이름을받았다: scalar triple product (또는 triple scalar product 또는 box product라고 언급된다). 기하학적으로 scalar triple product의 값은 세 개의 독립 벡터 u, v, w에 의해 만들어지는 평행육면체의(a parallelpiped) (양의) 부피와 일치한다. 동등하게, 그것은 u, v, w에 spanned 되는, 사면체의 부피의 6배이다. scalar triple product와 parallelepiped 사이의 관계는 그림 3.8에서 보여진다.
그 외적과 내적은 그 결과에 영향을 주는것 없이 triple product에서 교환될 수 있다:
스칼라 삼중적은 또한 그것의 세 개의 arguments의 cyclic permutation 하에서 변하지 않는다:
이러한 항등식 때문에, [u v w]라는 특별한 표기가 triple product를 나타내기 위해 종종 사용된다. 그것은 다음으로 정의된다
이 표기는 내적과 외적의 순서를 추상화하고, triple product identities의 올바른 부호를 기억하기 쉽도록 한다. 만약 그 벡터가 uvw를 왼쪽에서 오른쪽으로 읽는다면 (u에서 시작하여 wraparound를 허용하여), 그 product identity는 양수이고, 그렇지 않다면 음수이다:
스칼라 삼중적은 또한 3x3 행렬의 행렬식으로 표현될 수 있는데, 그 행(또는 열)이 벡터의 컴포넌트들이다:
세 개의 벡터들 u,v,w은 같은 평면에 놓여 있다 <=> 만약 [u v w] = 0이면.
3.3.8 Algebraic Identities Involving Scalar Triple Products
벡터들 u v w x y z가 주어진다면, 다음의 항등식들은 스칼라 삼중적에 유효하다:
3.4 Barycentric Coordinates(무게중심 좌표)
몇 가지 다른 교차 테스트에서 유용한 한 개념은 barycentric coordinates의 개념이다. Barycentric coordinates는 reference points들의 한 집합의 가중치 조합으로서 형성될 수 있는 공간을 파라미터화 한다. barycentric corodinates의 한 간단한 예제로서, 두 개의 점들 A와 B를고려해라. 그것들 사이의 선분에 있는 한 점 P는 P = A + t(B - A) = (1 - t)A + tB 또는 간단히 P = uA + vB이고 u + v = 1로 표현될 수 있다.
0<= u <= 1 이고 0<= v <=1이 <=> P는 선분 AB 위에 있다.
후자의 방식으로 쓰여진 (u,v)는 A와 B에 관련하여 P의 barycentric coordinates이다. A의 barycentric coordinates는 (1,0)이고, B에대해서 그것은 (0,1)이다.
bary 접두사는 그리스에서 오고, 무게를 의미한다. 접두사로서 그것을 사용하는 것은 선분 AB의 끝점들 A와 B에 배치된 무게로 u와 v를 고려하여 설명되어진다. 그러고나서, v:u의 비율로 선분을 나누는 점 Q는 centroid or barycenter이다: 이것은 가중치 선분의 무게중심(center of gravity) 그리고 그것이 균형잡히기 위해서 지지받아야할 위치이다.
무게중심 좌표의 일반적인 적용은 삼각형을 파라미터화 하는 것이다 (또는 삼각형들의 평면을). 세 개의 일직선이 아닌 점들 A, B, C로 명시된 삼각형 ABC를 고려해보자. 점들의 평면에 있는 어떤 점 P는 uniquely하게 P = uA + vB + wC로 표현되어질 수 있다. 어떤 상수 u, v, w에 대해서, 여기에서 u + v + w = 1이다. 그 triplet (u,v,w)는 그 점의 무게 중심 좌표와 일치한다. 그 삼각형 ABC에 대해서, 정점 A, B, C의 무게 중심 좌표가 각각 (1,0,0), (0,1,0), (0,0,1) 이다. 일반적으로, 무게 중심좌표 (u,v,w)가 있는 한 점은 0<= u,v,w <=1이라면 그 삼각형 안 또는 위에 있다. 대안적으로 0<= v <=1 , 0<=w <=1이고 v + w <=1 도 그렇다. 그 무게 중심 좌표는 그 평면이 P = uA + vB + wC가 P = A + v(B-A) + w(C-A)로 재공식화 되도록 따르는 것을 파라미터화 한다. v와 w는 임으로 되고 그래서
뒤의 공식에서, 두 개의 독립적인 방향 벡터 AB와 AC는 원점 A를가진 좌표계를 형성하는데, 그 평면에서 어떤 점 P가 v와 w의 관점에서 파라미터화 되로고 한다. 명백히, 무게중심 좌표계는 세 번째 컴포넌트가 처음 두 개의 관점에서 표현된다는 점에서, 중복되는 표기이다. 그것은 대칭성의 이유로 보존된다.
무게중심 좌표에 대해 풀기 위해서, 식 P = A + v(B-A) + w(C-A)가 동등히
v(B-A) + w(C-A) = P - A 이렇게 쓰일 수 있고,
가 된다. 이제 선형 방정식의 2x2 시스템이 양 변에 v_0과 v_1로 내적을 하여 형성될 수 있다:
그 내적은 linear operator이기 때문에, 이러한 수식들은 다음과 같다
이 연립방정식은 Cramer의 법칙으로 쉽게 풀린다. 다음의 코드는 이 방법을 사용하여 무게중심 좌표를 연산한 구현이다.
// Compute barycentric coordinates (u,v,w) for // point p with respect to triangle (a,b,c) void Barycentric(const glm::vec3 a, const glm::vec3 b, const glm::vec3 c, const glm::vec3 p, real& u, real& v, real& w { glm::vec3 v0 = b - a, v1 = c - 1, v2 = p - a; real d00 = glm::dot(v0, v0); real d01 = glm::dot(v0, v1); real d11 = glm::dot(v1, v1); real d20 = glm::dot(v2, v0); real d21 = glm::dot(v2, v1); float denom = d00 * d11 - d01 * d01; v = (d11 * d20 - d01 * d21) / denom; w = (d00 * d21 - d01 * d20) / denom; u = real(1.0) - v - w; }
만약 몇 가지 점들이 그 같은 삼각형에 대해 테스트된다면, 그 항들 d00, d01, d11과 denom은 오직 한 번만 연산되어야 한다, 그것들이 주어진 삼각형에 고정되어지기 때문이다.
무게 중심 좌표는 어떤 차원에서든지의 (Section 3.8) 한 simplex와 관련하여 한 점에 대해 연산되어질 수 있다. 예를들어, A,B,C,D 정점들로 명시된 4면체가 주어진다면, 무게 중심 좌표 (u,v,w,x)는 3D 공간에서 한 점 P를 다음으로 명시한다.
만약 0<= u,v,w,x <=1이라면, 그러면 P는 사면체 안에 있다.
A,B,C,D,P로 명시된 점들이 주어진다면, 무게 중심 좌표는 선형 연립방정식으로 설정하여 해결될 수 있다:
대안적으로, P = uA + vB + wC + xD의 양변으로부터 A를 빼서
이것은 4 개의 무게 중심 좌표중에 3개가 다음을 풀어서 얻어질 수 있다
(u = 1-v-w-x로 이어지는 4번째 component와 함께). 연립방정식 둘 중 하 나 어느 것이든 쉽게 Cramer's rule또는 가우스 소거법을 사용하여 쉽게 해결될 수 있다. 예를들어, 이전 시스템에서 그 좌표계는 Cramer's rule에 의해 다음의 비율로 주어진다
그리고 그 다음의 행렬식으로 표현된다
이러한행렬식들은 PBCD, APCD, ABPD, ABCP, ABCD 사면체의 양의 부피와 일치한다. (엄격히 각 양의 부피의 1/6). 앞서 보여 주었듯이, 그 비율은 반대 평면에 대한 그 점의 표준화된 상대 높이로 간단하게 한다.
삼각형으로 돌아가서, 사면체와 관련한 무게 중심 좌표가 부피의 비율로서 연산될 수 있듯이, 삼각형과 관련된 무게 중심좌표는 넓이의 비율로서 연산될 수 있다. 구체적으로, 한 주어진 점 P의 무게중심 좌표는 전체 삼각형 ABC의 넓이에 대해 PBC, PCA, PAB의 삼각형 넓이의 비율로 연산되어질 수 있다. 이 이유 때문에, 무게중심 좌표는 areal coordinates로 불려진다. 양의 삼각형 면적을사용하여, 이러한 수식들은 삼각형의 밖에 있는점들에 대해 또한 유효하다. 무게중심 좌표 (u,v,w)는 따라서 다음으로 주어진다
u = SignedArea(PBC) / SignedArea(ABC) v = SignedArea(PCA) / SignedArea(ABC), and w = SignedArea(PAB) / SignedArea(ABC) = 1 - u - v
constant factors들은 상쇄되기 때문에, 그 삼각형 넓이에 비례하는 어떤 함수든지 이러한 비율을 계산하는데 사용되어질 수 있다. 특히, 두 삼각형 변의 외적의 크기가 사용될 수 있다. 그 정확한 부호는 ABC의 이 외적의 내적을 취하여 유지된다. 예를들어, 삼각형 PBC에 대한 양의 넓이는 다음으로 연산된다
SignedArea(PBC) = Dot(Cross(B-P, C-P), Normalize(Cross(B-A, C-A)))
여기에서 상당히 짜증이 났는데, 실제로 삼각형 면적은 Cross 한 것의 0.5를 곱해주어야 한다. 왜냐하면 cross(A, B) = |A||B|sin(θ) 이기 때문이다.
그러나, 위의 면적들을 구하는 목적을 생각한다면, 비율을 구하는 것이기 때문에,
SignedArea가 1/2를 곱하지 않더라도, 비율로서 나눈다면 어차피 그것은상쇄되기 때문에 1/2를 곱하는 것을 제외해 버렸다. 글쓴이가 이것을 써놨다면 여기 코드를 빠르게 이해하고 넘어갔을텐데... 욕나오네
그리고 내가 예시를 따로 만들어서, 이 PBC 예제를 돌려봤는데, 음수의 값이 나왔다.
PBC가 아닌 PCB로 해야 올바른 값이 나왔다. 그래서 안되는 상황도 있으니 내 생각에는 그냥 면적구할려면 length 취해서 구하는게 좋을 것 같다.
여기에서는 legnth를 조금이라도 줄이기 위해 아마도, 저렇게 내적을 취해서 줄였겠지만, 안되는 상황도 있다. 일단 여기까지만 하고 넘어가자.
}
한 삼각형의 넓이가 base * height / 2로 쓰여질 수 있기 때문에, 그리고 이전의 비율 각각에 대해, 연관된 삼각형이 같은 base를 공유하기 때문에, 이전의 식들은 높이들의 비율로 간단화된다. 무게 중심좌표를 보는 또 다른 방법은 변들의 반대 정점의 높이를 기준으로한 BC, AC, AB의 변 각각에 대해 점 P의 표준화된 높이에 대응되는 컴포넌트 u, v, w로서 보는 것이다. 삼각형 ABC는 세 개의 2D 판들의 교차이기 떄문에 - 높이가 0에 있는 두 개의 평행한 선들 (또는 평면) 사이의 무한한 공간에 정의된 각 slab이다. 그리고 한 주어진 삼각형 변에 대해 높이는 1이고 - 그것은 또한 0 <= u,v,w <= 1이 한 점이 삼각형의 안에 있도록 요구되어지는 이유를 따른다 (그림 3.9).
한 삼각형의 변들과 일치하는 직선들은 또한 무게중심 좌표 컴포넌트의 부호들을 기반으로 7개의 무게중심 지역에서 삼각형의 평면들을 분해하는 것으로서 보여질 수 있다: 세 개의 변의 영역, 세 개의 정점 영역, 그리고 삼각형 내부 (그림 3.10) 이러한 영역들은 mesh traversla과 다양한 containment algorithms 둘 다에 연관이 있다.
무게 중심 좌표의 한 가지 중요한 특징은, 그것들이 projection 하에서 불변한다는 것이다. 이 특성은 이전에 주어진 것보다 좌표들을 계산하는 것의 잠재적으로 좀 더 효율적인 방식을 허용한다. 정점들의 3D 좌표들로부터 넓이를 계산하는 대신에, 그 계산은 모든 정점들을 xy, xz, or yz 평면에 사영하여 간단하게 될 수 있다. degeneracies를 피하기 위해, 그 projection은 그 사영된 넓이는 가장 큰 평면에 대해 되어야한다. 그 삼각형 normal의 가장 큰 absolute component value는 어떤 컴포넌트가 projection 동안 떨어져야 하는지를 가르쳐 준다.
inline float TriArea2D(real x1, real y1, real x2, real y2, real x3, real y3) { // Actually This is not correct Area // However for the purpose of getting the ratio, it's okay. return (x1 - x2) * (y2 - y3) - (x2 - x3) * (y1 - y2); } // Compute barycentric coordinates (u,v,w) for // point p with respect to triangle (a,b,c) void Barycentric(Point a, Point b, Point c, Point p, real& u, real&v, real& w) { // Unnormalized triangle normal glm::vec3 m = glm::cross(b - a, c - a); // Nominators and one-over-denominator for u and v ratios real nu, nv, ood; // Absolute components for determining projection plane real x = Abs(m.x), y = Abs(m.y), z = Abs(m.z); // Compute areas in plane of largest projection if(x >= y && x >= z) { // x is largest, project to the yz plane nu = TriArea2D(p.y, p.z, b.y, b.z, c.y, c.z); // Area of PBC in yz plane nv = TriArea2D(p.y, p.z, c.y, c.z, a.y, a.z); // Area of PCA in yz plane ood = real(1.0) / m.x; // 1 / (2 * area of ABC in yz plane) } else if (y >= x && y >= z) { // y is largest, project to the xz plane nu = TriArea2D(p.x, p.z, b.x, b.z, c.x, c.z); nv = TriArea2D(p.x, p.z, c.x, c.z, a.x, a.z); ood = real(1.0) / -m.y; } else { // z is largest, project to the xy plane nu = TriArea2D(p.x, p.y, b.x, b.y, c.x, c.y); nv = TriArea2D(p.x, p.y, c.x, c.y, a.x ,a.y); ood = real(1.0) / m.z; } u = nu * ood; v = nv * ood; w = real(1.0) - u - v; }
{
여기엔 수학적으로 많은 것들이 담겨 있는데, 차근차근 설명해보자.
먼저 TriArea2D는 내가 주석에 써놓았듯이, 실제 정확한 삼각형 넓이 공식이 아니다. 원래는 저 식에 0.5를 곱해야 한다. 하지만, 비율을 구하는 것이 목적이기 때문에, 그냥 나둔다. 이렇게 한 것 때문에 그 코드도 약간 바뀌게 된다.
그리고나서 삼각형의 넓이를 cross로 구한다.(사실 cross하고, 그 벡터 길이에 0.5를 곱해야 같다. 하지만, TriArea2D도 0.5를 곱하지 않았으므로, 비율을 구하는 것이기에 이제 같은 비율 선상에 있게 된다.)
이것을 통해 우리는 사영시킬 평면을 결정할 수 있는데, 이 평면을 결정하는 이유는 계산을 좀 더 간단하게 하기 위해서이다. 근데 어떤 평면을 고를지는 xy, yz, xz 중에서 고르는데, 삼각형 넓이를 cross하여 구할 때, 각 x,y,z 컴포넌트는 사실, yz평면에 사영한 삼각형 넓이, xz평면에 사영한 삼각형 넓이, xy평면에 사영한 삼각형의 넓이가 된다.
(여기서 2D의 perp dot product로 삼각형 넓이의 두배이다. 하지만 우리는 이제 삼각형 넓이의 * 2 한 것을 쓰기로 했으니 비율은 맞다)
너가 직접 손으로 표기해서 외적을 취한다면 그것을 알 수 있다.
어쨋든, 사영된 평면에서 삼각형의 넓이가 가장 큰 평면을 고르는 이유는 글쓴이는 degeneracies를 피하기 위해서라는데, 정확히 수학적인 어떤 이유가 있을 것이다. 어쨋든 사영된 삼각형의 넓이가 가장 큰 평면이 barycentric 좌표계의 특성으로 인해 barycentric 좌표들을 더 잘 계산할 수 있게 해주는 것 같다.
그래서 거기에서 사영된 평면에서의 삼각형 넓이들을 구하고, denominator는 m.x, -m.y, m.z를 역수 취하면 된다. 여기에서 -m.y인 이유는 cross에서 가운데 component -가 곱해지기 때문이다.
그래서 최종적으로 u, v, n을 구해준다.
}
무게 중심 좌표계는 많은 사용성을 갖는다. 그것들을 사영할 때 불변하기 때문에, 그것들은 다른 좌표계 사이에서 점들을 매핑시키는데 사용될 수 있다. 그것들은 point-in-triangle testing을 위해 사용될 수 있다. vertex-lit triangle이 주어진다면(정점에 color가 있는), 무게 중심 좌표계는 삼각형 내의 특정한 점에 대해 일치하는 RGB를 찾을 수 있다. 그 RGB는 그 삼각형에서 그 위치에 있는 한 오브젝트의 ambient color를 조정하기 위해 사용될 수 있다. triangle clipping에 대해, 그것들은 어떤 quantity를 interpolate하기 위해 ㅅ용될 수 있다 커러를 포함해서 (Gouraud shading), normals를 포함해서 (Phong shading), 텍스쳐 좌표를 포함해서 (texture mapping). 다음의 코드는 무게 중심 좌표계가 어떻게 삼각형 ABC에서 점 P가 포함되었는지를 테스트하기 위해 사용될 수 있는지를 보여준다.
// Test if point p is contained in triangle (a,b,c) int TestPointTriangle(Point p, Point a, Point b, Point c) { real u, v, w; Barycentric(a, b, c, p, u, v, w); return v >= real(0.0) && w >= real(0.0) && (v + w) <= real(1.0); }
irregular n-sided 볼록 polygons에 대해 무게 중심 좌표계의 일반화된 형태는 [Meyer 02]에서 주어진다. n = 3에 대해, 그것은 무시 중심 좌표계에 대해 전통적인 공식으로 줄인다. 또한 [Floater04]를 보아라.
점 P_0,... P_n과 관련한 한 점 P의 무게 중심 좌표계가 또한 a_0, ..., a_n >= 0을 만족할 때, P는 P_0, ... P_n의 convex combination이라고 말해진다.
3.5 Lines, Rays, and Segments
line L은 두 개의 임의의 이지만 구분되는 점들 A와 B의 linear combination으로 표현가능한 점들의 집합으로 정의될 수 있다:
여기에서, t는 모든 실수의 범위에 있따, -∞ < t < ∞. A와 B를 연결하는 line segment (또는 그냥 segment)는 A와 B를 지나는 선의 유한한 부분이고, t를 0 <= t <= 1의 범위에 놓도록 제한하여 주어진다. 선분은 끝점들 A와 B 유한의 순서로 주어진다면 방향이 지어진다. ray는 half-infinite line인데, 유사하게 정의되었지만, t >= 0으로 제한되어 진다. 그림 3.11은 line, ray, line segment 사이의 차이점을 보여준다.
그 직선을 parametric equation에서 항들을 재배치하여, 그 같은 표현은
L(t) = A + tv (where v = B - A)
가 얻어진다. 특히, Rays는 보통 이 형태로 정의된다. 두 개의 형태들은 직선의 parametric equation으로서 언급된다. 3D에서, 한 직선 L은 또한 implicitly하게, 다음을 만족하는 점들 X의 집합으로서 정의 될 수 있다
여기에서 A는 L 위에 있는 점이고, v는 L과 평행한 벡터이다. 이 항등식은 X - A가 v와 평행하다면, 그 외적이 zero vector result를 주기 때문에 따른다. (그 경우에, X는 L 위에 놓여있고, 그렇지 않다면 놓여있지 않다). 사실, v가 단위 벡터일 때, L로부터 점 p의 거리는
|| (P - A) X v|| 에 의해 주어진다. 이 식은 점들의 collinearity에 대해 검사와 관련있다. 거기에서 세 개 또는 그 이상의 점들은 그것들이 모두 같은 직선상에 놓일 때 collinear하다고 말해진다.
세 개의 점들 A, B, 그리고 C는 collinear하다 <-> 만약 삼각 ABC의 넓이가 0이라면
m = (B - A) X (C - A)라고 하자, collinearity는 ||m|| = 0인지를 체크하여 테스트 되어질 수 있다. 또는 square root를 피하기 위해 dot(m, m)이 0인지를 체크한다. 대안적으로 (m_x, m_y, m_z)가 m의 컴포넌트들이라면, 그 점들은 collinear 하는데 <=> |m_x| + |m_y| + |m_z| 가 0이면 그렇다.
3.6 Planes and Halfspaces
3D 공간에서 한 평면은 모든 방향에서 무한으로 확장하는 평평한 표면으로 고려될 수 있따. 그것은 몇 가지 다른 방식들로 묘사되어질 수 있다. 예를들어:
- 세 점들이 한 직선상에 있지 않다 (평면에서 삼각형을 만든다)
- normal과 그 평면위에 한 점
- normal과 원점으로 부터의 거리
첫 번째 경우에, 그 세 개의 점들 A, B, C는 평면 P의 parametric representation 이 다음으로 주어지도록 허용한다.
다른 두 경우에 대해, 그 plane normal은 그 평면에 어떤 벡터에도 수직인 nonzero vector이다. 주어진 평면에 대해, normal의 두 가지 가능한 선택들이 있다, 그것들은 반대 방향을 가리킨다. 세 개의 점들이 시계 반대 방향으로 되어 있고, 삼각형 ABC에 의해 명시된 한 평면을 볼 때, 그 convention은 plane normal을 바라보는 사람쪽으로 향한다. 이 경우에, 그 plane normal n은 외적 n = (B - A) X (C - A)으로 연산된다. 그 평면 밖으로 가리키는 normal로서 그 평면의 같은 면에 있는 점들은 그 평면의 앞에(front) 있다고 말해진다. 다른 면에 있는 점들은 그 평면의 뒤에(behind)에 있다고 말해진다.
normal n과 평면위의 한 점 P가 주어진다면, 평면위의 모든 점들 X는 n에 수직인 X - P 벡터에 의해 범주화된다. 이것은 두 개의 벡터의 내적이 0이 되는 것에 알려진다. 이 수직성은 평면에 대한 implicit equation을 발생시킨다, 그 평면의 point-normal form이다:
그 내적은 linear operator이고, 뺄셈 또는 덧셈에 대해 분배되도록 허용한다. 이 수식은 그러므로 n・X = d로 쓰여질 수 있고, 여기에서 d = n ・P이고, 이것은 평면의 constant-normal form이다. n이 단위벡터일 때, |d|는 원점으로부터 평면의 거리와 같다. 만약 n이 단위 벡터가 아닐 때, |d|는 여전히 거리이지만, n의 길이 단위에 있다. 절대값을 취하지 않을 때, d는 양의 거리로 해석된다.
평면의 방정식의 constant-normal form 종종 컴포넌트 별로 쓰여진다,
ax + by + cz - d = 0으로, 여기에서 n = (a, b, c)이고, X = (x, y, z)이다. 이 교재에서,
ax + by + cz - d = 0 형태가 그것의 공통된 대안식인 ax + by + cz + d =0보다 더 선호된다. 왜냐하면 그 전자가 필요하지 않은 negation을 제거하는 경향이 있기 때문이다 (예를들어, 평면과의 교차를 연산할 때).
한 평면이 미리 연산되어질 때, 평면 normal이 단위 벡터가 되도록 하는 것은 종종 유용하다. 그 평면 normal은 n을 ||n|| = root(a^2 + b^2 + c^2)으로 나누어서 단위 벡터로 만들어진다 (그리고 만약 이미 연산되었다면 d도). 단위 평면 normal를 갖는 것은 평면과 관련된 대부분의 연산들을 간단하게 한다. 이러한 경우에, 평면의 방정식은 normalized 되었다고 말해진다. 표준화된 평면 방정식이 한 주어진 점에 대해 evaluated될 때, 그 얻어진 결과는 평면으로 부터 그 점의 양의 거리이다 (만약 그 점이 평면 뒤에 있다면 음수이다, 그렇지 않다면 양수이고).
한 평면은 세 개의 noncollinear 점들로부터 연산되어질 수 있다 다음으로:
struct Plane { Vector n; // Plane noraml. Points x on the plane satisfy Dot(n, x) = d float d; // d = dot(n, p) for a given point p on the plane }; // Given three noncollinear points (ordered ccw), compute plane eqution Plane ComputePlane(Point a, Point b, Point c) { Plane p; p.n = Normalize(Cross(b - a, c - a)); p.d = Dot(P.n, a); return p; }
한 평면은 또한 parameterized form으로 주어질 수 있다
여기에서 u와 v는 평면의 두 개의 independent vectors이고, A는 평면의 한 점이다.
두 개의 평면들이 서로 평행이 아닐 때, 그것들은 한 직선에서 교차한다. 유사하게, 세 개의 평면들 - 서로 평행하지 않는 두 개의 평면들 - 한 점에서 교차한다. 두 개의 교차하는 평면 사이의 각은 dihedral angle이라고 언급된다.
임의의 차원에 있는 평면들은 hyperplanes라고 언급된다: 그것들이 있는 공간 보다 한 개 더 작은 차원을 가진 평면들이다. 2차원에서, hyperplane은 직선과 대응된다; 3D에서는 평면이다. 어떤 hyperplane은 그것이 들어있는 공간을 그 평면의 양 면에 있는 두 개의 무한한 점들의 집합으로 나눈다. 이러한 두 개의 집합들은 halfspaces(그림 3.12)로 언급된다. 만약 그 나누는 평면 위에 있는 점들이 halfspace에서 포함되었다고 고려된다면, 그 halfspace는 closed되었다 (그렇지 않다면 open되었다고 불려진다). positive halfspace는 그 plane normal가 가리키는 면에 놓여있고, negative halfspace는 그 평면의 반대면에 있다. 2D halfspace는 또한 halfplane이라고 불려진다.
3.7 Polygons
polygon은 n개의 변이 있는 closed figure이고, 평면에서 세 개 이상의 점들이 ordered set으로 정의되는데, 각 점이 다음과 선분으로 연결되어 있또록 한다 (그리고 마지막에서 처음으로). n개의 점들의 한 집합에 대해, 최종 폴리곤은 또한 n-sided polygon or 그냥 n-gon이라고 불린다. polygon boundary를 구성하는 그 선분들은 polygon sides or edges라고 불려지고, 그 점들 그자체로는 polygon vertices (단일로는, vertex)라고 불려진다. 두 개의 정점들은 그것들이 한 edge에 의해 연결되었다면 adjacent 하다. 그림 3.13은 한 폴리곤의 컴포넌트들을 보여준다.
한 폴리곤은 두 개의 어떠한 연속되지 않은 edges가 공통된 한 점을 갖지 않는다면 simple하다고 한다. 한 simple polygon은 그 평면을 두 개의 disjoint 부분으로 나눈다 : interior (polygon에 의해 덮여진 bounded area) 그리고 exterior (폴리곤의 밖에 있는 unbounded area). 보통 polygon이라는 용어는 polygon boundary와 interior 둘 다를 언급한다. polygon diagonal은 두 개의 폴리곤 vertices와 연결하고, 완전히 폴리곤 안에 놓여있는 선분이다. 한 vertex는 만약 interior angle이 180도 보다 작거나 같으면 (정점에 연결된 변 사이의 각도이다, 폴리곤 내부에서 측정된다), convex vertex이다. 만약 그 각이 180보다 더 크다면, 그것은 대신에 concave (or reflex) vertex라고 불려진다 (그림 3.14b).
한 폴리곤 P는 P의 어떤 두 점 사이의 모든 선분들이 완전히 P의 안에 있다면, convex polygon이다. convex가 아닌 polygon은 concave polygon이라고 불려진다. 한 개 이상의 concave vertices를 가진 한 폴리곤은 반드시 concave이지만, 오직 convex vertices만을 가진 한 폴리곤이 항상 convex인 것은 아니다 (다음 섹션을 보라). 삼각형은 항상 convex하다고 보장되어지는 유일한 n-sided polygon이다. Convex polygons은 평면에서 convex point sets의 부분집합으로서 보아질 수 있따. convex point set S는 점들의 집합인데, 거기에서 S에 있는 어떤 두 점 사이의 선분은 또한 S 안에 있다. a point set S가 주어진다면, S의 convex hull, CH(S)라고 표기되는데, S를 완전히 포함하는 가장작은 convex point set이다 (그림 3.15). CH(S)는 또한 S를 포함하는 모든 convex point sets의 intersection으로서 묘사되어질 수 있다.
affine hull AH(S)는 convex hull가 관련이 있다. affine hull은 S의 모든 점들을 포함하는 가장 낮은 차원의 hyperplane이다. 즉, 만약 S가 그냥 한 점만 포함한다면, AH(S)는 그 한 점이다; 만약 S가 두 점을 포함한다면, AH(S)는 그것들을 지나는 직선이다; 만약 S가 세 개의 noncollinear points를 포함한다면, AH(S)는 그것들에 의해 결정되는 평면이다; 그리고 만약 S가 4개 (또는 그 이상의) non-co-planar points를 포함한다면, AH(S)는 R^3의 모든 것이다.
explicit vertex representation 외에도, covex polygons은 또한 halfspaces의 무한한 개수의 교차로 묘사되어질 수 있다. 이 표기는 예를들어 point containment tests에 대해 편리하다. implicit polygon representation에 대해, 만약 한 점이 모든 halfspaces에 놓여있다면, 한 점은 폴리곤 안에 놓여있는 것이다. 그림 3.16은 세 개의 halfspaces의 교차로서 표현된 한 삼각형을 보여준다. point set convexity에 대한 대안의 정의는 그러므로,
한 point set S가 convex하다 <=> S가 S를 완전히 포함하는 모든 halfspaces의 intersection과 동일한다면.
polygons에 대해 (그리고 polyhedra에 대해), 이것은 그것이 직접적으로 convexity test를 구현하기 위해 사용될 수 있다는 의미에서 operative definition이다.
두 개 이상의 폴리곤들은 polygon mesh을 만들기 위해서 그것들의 edges에서 연결되어질 수 있다. 한 polygon mesh에서, 한 정점의 degree는 그 정점에 연결된 edges의 개수와 일치한다. 이 교재에서, 만약 모든 폴리곤들이 each edge가 정확히 두 개의 폴리곤의 부분이도록 되기 위해서 연결되었다면 한 mesh는 closed되었다고 고려될 것이다.
3.7.1 Testing Polygonal Convexity
충돌 탐지 시스템에서 폴리곤에 대해 수행되는 Most intersection tests와 다른 연산들은 concave polygons 보다 convex에 적용될 때 더 빠르다. 가정을 간단하게 하는 것이 그 전자의 케이스에서 만들어질 수 있다는 점에서. 삼각형은 이 점에서 훌륭하다. 왜냐하면 그것들은 convex하다고 보장되는 유일한 폴리곤의 유형이기 때문이다. 그러나, 같은 지역을 덮는 multiple triangles에 대해서 보다, single convex n-gon에 대해 intersection을 수행하는 것이 더 효율적일지도 모른다. 어떠한 concave faces가 없도록 보장하는 것은 collision geometry database에서 존재한다 -그것은 더 빠른 테스트와 작동하지 않을 것이다, 특히 convex faces를 위해 쓰인 - 모든 faces들은 convex로서 입증되어야 한다, tool time or 런타임 동안에 아마도 디버그 빌드에서.
자주, 사각형(or quads, 짧게 해서) 삼각형 외에도 지원되는 유일한 primitives이다. 그러한 상황들에서, 임의의 폴리곤에 대해 generic convexity test를 적용하기 보다는, 특정하게 quads에 적용되는 더 간단한 convexity test를 수행하는 것이 사용될 수 있따. quad ABCD의 모든 정점들이 같은 평면에 있다고 가정하여, 그 quad는 convex하다 <=> 그것의 두 개의 대각선이 완전히 그 quad의 내부에 놓여있다면 (그림 3.17 a에서 c). 이 테스트는 대각선과 일치하는 두 선분 AC와 BD가 서로 교차하는지를 테스트하는 것과 같다. 만약 그렇다면, 그 quad는 convex이다. 만약 그렇지 않다면 quad는 concave하거나, self-inetsecting이다. 만약 그 선분들이 평행하고 겹친다면, 그 quad는 degenerate된다 (직선으로), 그림 3.17d에서 그려지듯이. 세 개의 collinear vertices가 있는 한 quad가 convex라고 고려하는 것을 피하기 위해서, 만약 선분들이 그것들의 내부에서 겹친다면 (그리고 그것들의 바깥점에서가 아닌) 그 선분들은 오직 교차한다고 고려되어야만 한다.
선분들의 교차는 BD를 지나는 직선의 반대편에 놓여 있는 점 A와 C와 같다, 뿐만 아니라 AC를 지나는 직선의 반대편에 놓여있는 점 B와 D와 같다. 차례로, 이 테스트는 BDC와 반대 순서로 감기는 삼각형 BDA와 같고, ACB와 반대로 감기는 ACD와 같다. 그 반대 winding은 삼각형의 normals을 연산하고 삼각형들의 normal 사이의 내적의 부호를 비교하여 탐지되어질 수 있다. 만약 그 내적이 음수라면, 즉, normals가 반대 방향을 가리킨다면, 그 삼각형 그러므로 반대 방향으로 감긴다. 요약해서 그 사각형은 convex하다 만약
{
교재에 그려진 사각형 ABCD 순서대로 그려야 이 식이 이해가 된다. 잘 못 점을 찍으면 이 식이 안맞는다. 사각형 점 찍는 방법은 한 점에서 시작하여 시계 반대방향으로 순서대로 찍는 것이다.
}
간단한 구현은 다음의 코드를 만들어 낸다:
// Test if quadrilateral (a, b, c, d) is convex int IsConvexQuad(Point a, Point b, Point c, Point d) { // Quad is nonconvex if Dot(Cross(bd,ba), Cross(bd, bc)) >= 0 Vector bda = Cross(d - b, a - b); Vector bdc = Cross(d - b, c - b); if(Dot(bda, bdc) >= 0.0f) return 0; // Quad is now convex iff Dot(Cross(ac, ad), Cross(ac, ab)) < 0 Vector acd = Cross(c - a, d - a); Vector acb = Cross(c - a, b - a); return Dot(acd, acb) < 0.0f; }
평면에서 두 개의 선분들을 intersection에 대해 테스트하는 것은 좀 더 세부적으로 Section 5.1.9.1에서 이야기 된다.
일반적인 n-gons에 대해, quads가 아닌, 간단한 솔루션은 각 폴리곤 edge에 대해, 모든 다른 정점들이 (엄격히) 그 edge의 같은 면에 놓여있는지를 보는 것이다. 만약 그 테스트가 모든 edges에 대해 사실이라면, 그 폴리곤은 convex이고, 그렇지 않다면 concave하다. 일치하는 정점에 대한 분리된 check가 그 테스트를 튼튼하게 만들기 위해 요구된다. 그러나, 구현하기에 쉬울지라도, 이 테스트는 큰 폴리곤에 대해 매우 비싸다. 정점들의 개수에 따라 O(n^2)의 복잡도를 가진다. 충돌 탐지 시스템과 관련된 폴리곤들은 거의 크지 않아서, O(n^2)의 복잡도는 문제가 된다. 더 빠른 테스트들을 생각해내는 것은 쉽다. 그러나, 그것들 대부분은 convex polygons의 부분집합을 분류하고, 부정확하게 몇 가지 nonconvex polygons들을 분류한다 (그림 3.18) 예를들어, 엄격히 convex polygon은 180보다 작은 내부 각을 갖는다. 그러나, 이 테스트가 convexity에 대한 필수적인 척도일지라도, 충분한 것은 아니다. 내부 각을 단독으로 테스트하는 것은 따라서 부정확하게 펜타그램이 convex polygon이라는 것을 결론지을 것이다 (그림 3.18c) 이 테스트는 오직 polygon이 미리 self-intersecting 하지 않는다고 알려져야만 유효하다.
convexity test에 대한 또 다른 basis는 어떤 주어진 축을 따라서 방향에서 두 개의 변화가 있따, 한 convex polygon의 정정마다 움직일 때, 이것은 첫 번째에서 마지막 정점으로의 wraparound를 설명한다. 그림 3.18d에서 zigzag case를 탐지하기 위해 방향의 변화에 대한 테스트가 수행되어야 한다, 두 개의 다른 방향에 대해, x축과 y축 둘 다에 따라서. 비록 겉보기에는 튼튼해 보일지라도, 이 테스트는 (예를들어) 원래 convex polygon의 모든 정점들이 한 단일의 직선에 사영될 때 실패한다. 이러한 두 대안을 둘 다를 동시에 적용하는 것은 오히려 튼튼한 결합된 테스트를 만들어낸다는 것이 밝혀졌따, 서로를 엄호해주는 두 가지 접근법과 함께. 그 결합된 테스트의 한 구현은 [Schron94]에 묘사된다.
3.8 Polyhedra
polyhedron(다면체)은 polygon의 3D 형이다. 그것은 다면의 solid의 모양에서 공간의 bounded and connected region이다. 다면체 boundary는 많은 (flat) polygonal faces로 구성된다. 그것은 각 polygon edge가 정확히 두 개의 faces들의 부분이 되도록 연결되어졌다. 다면체의 몇 가지 다른 정의들은 그것이 unbounded되게 한다; 즉, 어떤 방향들로 무한히 연장되게 한다.
polygons에 대해, polyhedron boundary는 공간을 두 개의 분리된 영역으로 나눈다: interior and exterior. polyhedron은 만약 그것의 interior과 boundary에 의해 결정되는 point set이 convex하다면 convex하다. (bounded) convex polyhedron은 또한 polytope라고 언급된다. 폴리곤처럼, polytopes는 또한 유한한 개수의 halfspaces의 교차로서 묘사되어질 수 있다.
d-simplex는 d-차원 공간에서 d + 1개의 affinely하게 독립된 점들의 convex hull이다. simplex는 (복수형 simplices) 어떤 주어진 d에 대해 d-simplex이다. 예를들어, 0-simplex는 한 점이고, 1-simplex는 선분, 2-simplex는 삼각형, 3-simplex는 사면체 (그림 3.20)이다. 한 simplex는 그것의 정의되는 집합으로부터 한 점을 제거하는 것이 그 simplex의 차원성을 하나씩 제거하는 특성을 갖는다.
일반적인 convex set C에 대해 (따라서, 반드시 polytope가 아닌), 한 주어진 방향으로부터 가장 멀리있는 그 집합으로부터 한 점은 C의 supporting point라고 불려진다. 좀 더 구체적으로, 만약 한 주어진 방향 d에 대해 P가 d・P = max{d・V: V in C}가 유효하다면. P는 C의 supporting point이다; 즉, P는 d・P가 가장 큰 점이다. 그림 3.21은 두 개의 다른 convex sets에 대해 supporting points를 보여준다. Supporting points는 가끔씩 extreme points라고 불려진다. 그것들은 반드시 unique하지 않다. polytope에 대해, 그것의 정점들 중 하나는 항상 한 주어진 방향에 대해 supporting point로서 선택되어질 수 있다. 한 support point가 vertex일 때, 그 점은 보통 supporting vertex라고 불려진다.
support mapping (or support function)은 한 함수 S_c(d)인데, 방향 d를 C의 supporting point로 매핑시키는 convex set C와 관련있다. simple convex shapes에 대해 - 구, 박스, 원뿔, 실린더 같은 - support mapping은 closed form으로 주어질 수 있다. 예를들어, 원점이 O인 구 C에 대해, 반지름은 r이고, support mapping은 S_c(d) = O + rd/||d|| 로 주어진다. (그림 3.21b) 더 높은 complexity의 Convex shapes는 suppport mapping function이 numerical methods를 사용하여 supporting point를 결정하는 것을 요구한다.
n개의 정점을 가진 polytope에 대해, supporting vertex는 자명하게 모든 정점에 대해 탐색하여 O(n) time으로 찾아진다. 각 정점에 대해 이웃한 모든 인접 정적을 열겨한 자료구조를 가정하여, extreme vertex는 단순한 hill-climbing algorithm을 통해 발견되어질 수 있다, 그리고 그것은 greedily하게 정점을 점 더 extreme하게 방문한다, 어떠한 더 extreme 정점이 발견되지 않을 때 까지. 이 접근법을 매우 효율적이다. 왜냐하면 그것은 오직 그것이 그 extreme vertex를 움직일 때 , 정점들의 오직 small corridor만을 방문하기 때문이다. 더 큰 polyhedra에 대해, hill climbing은 한 vertex에 대해 인접리스트에 한 개 이상의 인공 이웃을 추가하여 가속될 수 있다. 정점들의 hierarchical representation의 precomputation을 통해, supporting point를 O(logn) 시간에 찾는 것이 가능하다. supporting vertices에 대해 탐색을 가속시키는 이러한 아이디어들은 Chapter 9에서 더 정교해진다.
supporting plane은 plane normal로서 주어진 방향이 있는 support point를 지나는 평면이다. 만약 모든 polytope 정점들이 polytope centroid로서 그 평면의 같은 면에 놓여있다면 한 평면은 polytope를 supporting하고 있다. 정점 집합 {P_1, ... P_n}으로 정의되는 polytope의 centroid는 정점들의 위치의 artihmetic mean이다: (P_1 + ,,, + P_n)/n.
두 개의 convex sets의 separating plane은 한 집합이 완전히 positive (open) halfspace에 있고, 다른 것이 완전히 negative (open) halfspace에 있게 하는 한 평면이다. separating plane에 직교하는 한 축은 (그것의 normal에 평행한) separating axis라고 불려진다. 두 개의 교차하지 않는 convex sets에 대해, separating axis(또는 평면)는 항상 존재한다고 보여질 수 있다. 그러나, concave sets에 대해 그 같은 것은 필수적으로 사실이 아니다. Separating axes는 Chapter 5에서 좀 더 상세히 재방문된다.
polyheron의 표면은 종종 2-manifold라고 언급된다. 이 topological 용어는 그 표면의 각 점의 이웃이 한 disk에 대해 topologically equivalent하다 (또는 homeomorphic). 2-manifold인 polyhedron surface는 polyhedron의 한 edge가 정확히 두 개의 면(faces)에 연결된다고 암시한다( 또는 그 edge에 있는 한 점의 이웃이 disk-like하지 않다).
한 다면체의 정점들 (V), 면 (F), 변(E)의 개수는 Euler 공식 V + F - E = 2와 연관된다. 구멍이 있는 polyhedra에 대해 유효하게 하기 위해 Euler formula를 일반화하는 것이 가능하다. Euler formula는 Chapter 12에서 다시 방문된다.
3.8.1 Testing Polyhedral Convexity
polygon에 대한 convexity test와 유사하게, polyhedron P는 convex하다 <=> P의 모든 faces에 대해, P의 모든 정점들이 (엄격히) 그 면의 같은 면에 놓여 있따면. coincident vertices와 polyheron faces의 collinear edges에 대한 separate test는 그 테스트를 튼튼하게 만들기 위해 요구된다, 보통 coincidency와 collinearity를 결정하기 위해 더해진 어떤 tolerance도 함께 있다. 이 테스트의 복잡도는 O(n^2)이다.
더 빠른 O(n) 접근법은 P의 각 면 F에 대해 F의 centroid C를 연산하는 것이다, 그리고 F의 모든 이웃한 면들 G에 대해, C가 G의 supporting plane 뒤에 놓여있는지를 테스트한다. 만약 어떤 C가 한 개 이상의 이웃한 면들의 supporting plane의 뒤에 놓여있는 것에 실패한다면, P는 concave이고, 그렇지 않다면 convex하다고 가정된다. 그러나, 대응되는 polygonal convexity test가 pentagram에 대해 실패할지도 모르는 것처럼, 이 테스트도 실패할지도 모른다, ~
3.9 Computing Convex Hulls
다른 사용성 가운데, convex hulls는 collision geometry를 위한 tight bounding volumes으로서 역할을 할 수 있다. Convex hulls을 연산하는데 많은 다른 알고리즘들이 제안되었다. 그것들 중 두 개가 다음 두 섹션에서 간단히 설명된다 : Andrew's algorithm and Quickhull algorithm.
3.9.1 Andrew's Algorithm
2D convex hull 알고리즘을 구현하기에 가장 튼튼하고 쉬운 것 주우 하나는 Andrew's algorithm이다 [Andrew79]. 그것의 첫 번째 pass에서, 그것은 주어진 점 set에서 모든 점들을 왼쪽에서 오른쪽으로 정렬하여 시작한다. 차후의 second and third passes에서, 가장 왼쪽에서 가장 오른쪽점으로 가는 edges의 chains가 형성되는데, 이것은 개별적으로 convex hull의 upper half와 lower half와 대응된다. chains가 만들어지고, 그 hull은 간단히 두 chains의 끝과 끝을 연결해서 얻어진다. 그 과정은 그림 3.22에서 보여진다. 그 주된 step은 hull edges의 chains을 만드는 것에 있다. 그 chains들 중 하나가 어떻게 형성되는지 보기 위해, 점들의 부분적으로 구성된 upper chain을 보아라, middle left-hand에 그림에서 보여지듯이. 그 presentation을 간단하게 하기 위해, 같은 x 좌표에 여러 점들이 없다고 가정된다 ( 이 가정은 나중에 들어온다).
초기에, 두 개의 가장 왼쪽의 점들 A와 B가 그 chain의 첫 번째 edge를 만들기 위해 취해진다. 그 나머지 점들은 이제 순서대로 계속해서 처리되고, 그 hull chain에 추가를 위해 하나씩 고려된다. 만약 고려를 위해 다음 점이 그 chain의 현재 마지막 edge의 오른쪽에 놓여 있다면, 그 점은 시험적으로 hull의 가정된 부분이고, 그 chain에 추가된다. 그러나, 만약 그 다음 점이 그 chain의 현재 마지막 변의 왼쪽에 놓여있다면, 이 점은 명백히 hull의 바깥에 놓여있고, hull chain은 에러임에 틀림없다. 체인에 추가되는 마지막 점은 그러므로 제거되고, 그 테스트는 다시 적용된다. 체인으로부터 점들을 제거하는 것은 다음 점이 chain의 마지막 edge의 오른쪽에 놓일 때 까지 계속된다. 그리고 그 후에, 그 다음점은 hull chain에 추가된다.
예제에서 그 다음점은 점 C이다. C는 edge AB의 왼쪽에 놓여있다. 따라서, tentative hull은 에러이며, B는 chain으로부터 제거된다. 제거할 더 이상의 점이 없기 때문에 (A는 hull에 놓여있고, 가장 왼쪽의 점이다), C는 chain에 추가되고, hull chain A - C를 만든다. 다음은 점 D인데, edge Ac의 오른쪽에 놓여있고, 그러므로 체인에 추가된다.
~~~~
그러고나서 남은 것은 같은 x좌표를 공유하는 많은 점들의 경우를 다루는 것이다. 간단한 해결책은 upper chain에서 가자 위에 있는 점들을 고려하여 더하는 것이고, lower chain에 대해, 가장 아래에 있는 점을 고려하여 더하는 것이다.
Andrew 알골즘의 in-situ 버전을 쓰는 것은 쉽다. 따라서, 배열로 표현되는 점들의 집합에 이익이 있이 사용되어질 수 있다.
3.9.2 The Quickhull Algorithm
비록 Andrew의 알고리즘이 2D에서 잘 작동할지라도, 3D에서 그것을 작동하도록 어떻게 연장시킬지는 즉시 명백하지 않다. 2D와 3D 둘 다에서 작동하는 대안의 방법은 Quickhull algorithm이다. Quickhull algorithm의 기본 아이디어는 매우 간단하고, 2D 케이스에 대해 그림 3.23에서 보여진다.
첫 번째 단계에서, 점 집합의 bounding box가 얻어지고, 일반적인 경우에, 그 집합의 4개의 extreme points가 찾아진다 (bounding box의 4개의 변에 각각에 놓여있는). 이러한 점들은 extreme이기 때문에, 그것들은 convex hull에 놓여있어야만 한다. 따라서 convex hull의 quadrilateral "first approximation"을 형성한다 (끄림 3.23, top left). 그러듯이, 이 quadrilateral안에 놓여있는 어떤 점들은 명백히 그 점 집합의 convex hull에 놓일 수 없고, 나중의 고려에서 제거되어야 한다 (그림 3.23, top right). 그러나, quadrilateral 밖에 놓여있는 어떤 점들은 hull에 놓여야 하고, 그 approximation은 이제 정제된다. 사각형의 각 변에 대해, 그 edge로부터 가장 멀리 있는 변 밖에 있는 점이 찾아진다. 각 그러한 점이 그 변으로부터 수직 방향으로 extreme하기 때문에, 그것은 hull에 놓여있어야 만 한다. 그러므로, 이러한 점들은 hull에 삽입된다, 그것들이 밖에 있는 edge의 점들의 두 개 사이에 (그림 3.23 bottom left). 그 edge의 endpoints과 함께, 이러한 새로운 points들은 triangular region을 만든다. 이전 처럼, 이 영역 안에 있는 어떤 점들은 hull위에 있을 수 없고, 버려진다 (그림 3.23 bottom right). 그 절차는 재귀적으로 hull에 추가되었던 각 새로운 edge에 대해 그 같은 절차를 반복한다. 그리고 edges 밖에 어떠한 점도 없을 때 재귀를 제거한다.
이전 문단이 전에 알고리즘 설명을 완료지었을 지라도, 두 가지 사소한 복잡성은 탄탄한 구현에서 다뤄져야 한다. 그 첫 번째 복잡성은 초기 hull approximation이 항상 quadrilateral이 아니라는 것이다. 만약 한 extreme point가 bottom left-hand corner에 놓여있따면, 초기 도형은 삼각형 일지도 모른다. 만약 다른 extreme point가 top right-hand corner에 있다면, 그것은 degenerate hull일 지도 모른다, 오직 두 개의 점들만으로 구성되고. 문제들을 피하기 위해, 다양한 개 수의 edges의 초기 hull approximation를 처리하기 위해 한 구현이 쓰여져야만 한다. 두 번째 복잡성은 초기 bounding box의 edge에서 단일의 unique point가 없을지도 모른다, 또는 한 edge로부터 가장 멀리있는 single unique point가. 주어진 bouding box edge에서 몇 가지 점들이 있을지도 모르고, 한 edge로부터 동일하게 먼 점들이 있을지도 모른다. 두 경우에, 그 edge endpoints에 가장 가까이 놓여있는 두 개의 점들 중 하나가 extreme point로서 선택되어야 한다. 이러한 두 점들 사이에 놓여있는 어떤 점들은 일반적으로 convex hull의 정점으로고려되지않는다. 그것들이 edge 위에, 그러니까 edge의 end vertices와 collinear하기 때문이다.
두 점들 A와 B에 의해 명시된 한 edge가 주어진다면, 그 edge로부터 가장 멀리있는 한 점 집합 P의 점은 그 점을 그 edge에 수직인 것에 점들을 사영해서 찾아질수 있다. 수직인 것을 따라 가장 멀리 사영된 점이 찾는 점이다. 수직인 것을 따라 동일하게 먼 두 점 사이의 ties를 깨기 위해, AB를 따라 가장 멀리 사영하는 것이 가장 멀리 있는 점으로 선택된다. 이 점은 다음의 코드를 통해 보여진다:
// Return index i of point p[i] farthest from the edge ab, to the left of the edge int PointFarthestFromEdge(Point2D, a, Point2D, b, Point2D p[], int n) { // Create edge vector and vector (counterclockwise penpendicular to it Vector2D e = b - a, eperp = Vector2D(-e.y, e.x); // Track index, 'distance' and 'rightmostness'of currently best point int bestIndex = -1; float maxVal = -FLT_MAX, rightMostVal = -FLT_MAX; // Test all points to find the one farthest from edge ab on the left side for(int i = 1; i < n; ++i) { float d = Dot2D(p[i] - a, eperp); // d is proportional to distance along eperp float r = Dot2D(p[i] - a, e); // r is proportional to distance along e) if(d > maxVal || (d == maxVal && r > rightMostVal)) { bestIndex = i; maxVal = d; rightMostVal = r; } } return bestIndex; }
Quickhull algorithm은 또한 3차원에서 작동하도록 만들어질 수 있다 (그리고 더 높은 차원에서) [Barber96]. 3D에서, 초기 approximation은 point set을 제한하는 axis-aligned box에 놓여있는 6개(까지의) extreme points로 시작한다. 이제, 폴리곤의 변들로부터 가장 멀리있는 점들을 찾는 대신에, polyheron의 면들로부터 가장 멀리있는 점들이 찾아진다. 그 폴리곤들 edges들을 새로운 점이 hull에 넣어질 때 마다 분해하는 대신에, polyhedron faces는 두 개 이상의 면들로 분해된다.
Quickhull algorithm의 solid implementation인 ,Qhull by Brad Barber는 인터넷에서 다운로드할 수 있다. 일반적으로 Convex hull algorithms은 좀 더 세부적으로 [O'Rourke98]에서 설명된다.
3.10 Voronoi Regions
많은 교차테스트의 설계에 있어서 중요한 한 개념은 Voronoi regions의 개념이다. 평면에서 점들의 한 집합 S가 주어진다면, S에 있는 한 점 P의 Voronoi region은 S에 있는 어떤 다른 점들 보다 P에 (거의 가까운) 더 가까운 평면에 있는 점들의 집합으로서 정의된다. Voronoi regions과 그 밀접하게 관련된 Voronoi diagrams (S에서 두 개 이상의 점들과 동일하게 가까운 점들의 집합을 묘사한다)은 computational geometry의 분야에서 온다. 거기에서 그것들은 가장 가까운 이웃 queries를 위해 사용된다, 다른 사용성 중에서.
Voronoi regions의 개념을 조금 확장시켜서, 그것은 충돌 탐지 프로그램에 대해 꽤 유용해진다. polyheron P가 주어진다면, P의 feature는 그것의 vertices, edges, or faces의 중의 하나가 된다. P의 feature F의 Voronoi region은 그러고나서 P의 어떤 다른 feature보다 F에 (또는 거의 가까운) 공간에서의 점들의 집합이 된다. 그림 3.24는 한 삼각형의 features에 의해 결정된 Voronoi regions를 보여준다. 한 정육면체의 Voronoi feature regions의 세 가지 유형은 그림 3.25에서 그려진다. Voronoi region이라는 용어와 Voronoi feature region이라는 용어는 이 책에서 상호교환하여 사용된다. Voronoi regions과 섹션 3.4에서 이야기된 barycentric regions과 혼동하지 않는 것이 중요하다. Voronoi region의 boundary planes은 Voronoi planes라고 언급된다.
한 convex polyheron P가 주어진다면, P의 외부에 있는 공간에서의 모든 점들은 P의 vertex, edge, or face의 Voronoi feature region에 놓여있다고 분류된다. 그리고 이 때 두 개의 인접합 Voronoi feature regions사이의 boundary는 그 영역들 중 오직 하나에만 속한다고 고려된다. Voronoi regions은 polyheron 외부의 공간의 분할을 만들어내기 때문에, 그것들은 예를들어, 공간에서 어떤 점 Q에 대해 convex polyhedral object에 있는 가장 가까운 점을 결정하기 위해 사용될 수 있다. 이 결정은 Q가 region의 안에 있다고 발견될 때 까지 region마다 확인하여 처리된다. object에서 Q에 가장 가까운 점은 그러고나서 주어진 region이 관련된 feature에 Q를 사영시키는 것이다. 반복된 queries에 대해, 프레임마다 어떤 region에 가장 가까운 점이 있는지를 기억하여 coherence를 이용하고, 거기에서 부터 새로운 탐색을 시작하는 것이 가능하다. Voronoi regions의 개념은 Chapter 5에서 설명되는 여러가지 교차 테스트에서 사용된다. Voronoi regions는 또한 Chapter 9에서 이야기되고,, convex polyhedra의 context of intersection에서 이야기 된다.
3.11 Minkowski Sum and Difference
점들의 집합에 대한 두 가지 중요한 연산들이 이 책의 부분들 도처에서 언급될 것이다. 이러한 연산들은 점들의 집합에 대한 Minkowski sum과 Minkowski difference이다. A와 B가 두 점들의 집합이라고 하자, 그리고 A와 B에 있는 점들의 쌍에 대응되는 위치 벡터를 a와 b라고 하자. Minkowski sum인 A⊕B는 다음의 집합으로 정의된다
A⊕B = {a + b : a ∊ A, b ∊ B}
a + b는 포지션 벡터 a와 b의 벡터 합이다. 시각적으로, Minkowski sum은 B에 있는 모든 점으로 (또는 역으로) 평행이돈된 A에의해 휩쓸고 간 영역이로 보여질 수 있다. Minkowski sum의 그림은 그림 3.26에서 제공된다.
두 점들의 집합 A와 B의 Minkowski Difference는 Minkowski Sum과 유사하게 정의된다:
A⊝B = {a - b : a ∊ A, b ∊ B}
기하학적으로, Minkowski difference는 원점에 대한 B의 반사에 A를 더하여 얻어진다; 즉,
A ⊝ B = A ⊕ (-B)이다 (그림 3.27(. 이 이유 때문에, 두 항들은 종종 Minkowski sum으로 언급된다. 두 개의 convex polygons에 대해, P와 Q, Minkowski sum R = P + Q는, R이 convex polygon이고, R의 정점들이 P와 Q의 정점들의 합이라는 특성을 가진다. 두 개의 COnvex polyhedra의 Minkowski sum은 convex polyhedron이고, 일치하는 특성을 갖는다.
Minkowski sums은 충돌탐지에 직접적으로 그리고 간접적으로 둘 다 적용된다. 복잡한 오브젝트가 많은 다른 동일하게 복잡한 장애물들을 지나가는 문제를 고려해보자. 이러한 복잡한 오브젝트들에 대한 비싼 테스트를 수행하는 대신에, 그 장애물들은 그 오브젝트가 "줄어드는" 동시에 그 오브젝트가 "성장해질" 수 있다. 이것은 움직이는 오브젝트에 대한 충돌 테스트가 커진 장애물에 대한 움직이는 점으로서 다루어지게 한다. 이 아이디어는 예를들어 BSP 트리와 관련하여 Chapter 8에서 탐구될 것이다.
Minkowski difference는 충돌 탐지 관점에서 중요하다, 왜냐하면 두 점 집합 A와 B가 충돌하는데 (즉, 한 개 이상의 점들이 겹친다) <=> 그것들의 Minkowski diffrence C (C = A - B)가 원점을 포함한다면이다 (그림 3.27). 사실, 훨씬 더 강한 결과를 만드는 것이 가능하다: A와 B사이에 최단 거리를 연산하는 것은 C와 원점 사이의 최단 거리를 연산하는 것과 같다. 이 사실은 Chapter 9에서 보여지는 GJK 알고리즘에서 활용된다. 그 결과는
이기 때문에 그렇다. 두 convex ets의 Minkowski difference가 또한convex set이고 따라서 그것의 최소 기준의 점도 유일하다는 것에 주목해라.
Minkowski sum을 explicitly하게 연산하는 알고리즘이 있다 (예를들어, [Bekker01]. 그러나, 이 책에서 Minkowski sum은 우선적으로 개념적으로 사용된다, 충돌 문제를 동일한문제로 다시 casting하는 것을 돕기위해서. 때떄로, GJK알고리즘에서 처럼, 두 오브젝트들의 Minkowski sum이 implictly하게 연산된다.
두 오브젝트들의 Minkowski difference는 가끔씩 translational configuration space obstacle (or TCSO)로 언급된다. TCSO에 대한 queries는 configuration space에서 수행된다고 말해진다.
3.12 Summary
충돌 탐지 분야에서 작업하는 것은 기하학과 선형대수에 대한 튼튼한 이해를 요구한다, 일반적으로 수학은 말할 것도 없고. 이 챕터에서 이러한 분야로부터의 몇 가지 개념들을 리뷰했고, 이것들은 이 책에 스며든다. 특히, 내적, 외적, 스칼라 삼중적의 특성을 이해하는 것이 중요하다. 왜냐하면 이러한 것들이 예를들어, 가상적으로 모든 primitive intersection test의 유도에서 사용되기 때문이다 (Chapter 5를 비교해라). 이러한 수학개념에 편함을 느끼지 않는 독자들은 선형 대수 교과서를 참고하길 원할 것이다, chapter introduction에서 언급된 것들 같은.
이 챕터는 또한 많은 기하학적 개념들, 점, 직선, rays, segments, 평면, halfspaces, polygons, and polyhedra를 포함하여 보았었다. 이러한 것들과 다른 기하학적 개념에 대한 기쁜 도입은 [Mortenson99]에서 주어진다.
computational geometry와 convex sets의 이론으로부터 나온 관련된 개념들은 또한 보아졌다. Voronoi regions은 가장 가까운 점들의 연산에서 중요하다. 교차하지 않는 convex objects들에 대한 separating planes과 axes의 존재는 이러한 오브젝트들의 분리에 대해 효율적인 테스트를 가능하게 한다, 그리고 chapter 5와 9에서 더 이야기 된다. Minkowski sum과 difference operations은 어떤 충돌 탐지 문제가 다른 형태로 recast되도록 하고, 이것은 연산하기에 더 쉬워진다. Chapter5와 9는 그러한 변형을 또한 이야기 한다.
computational geometry의 분야에 대한 좋은 입문서는 [O'Rourke98]이다. convex sets의 이론은 (convex optimization의 맥락에서) [Boyd04]에서 이야기된다.

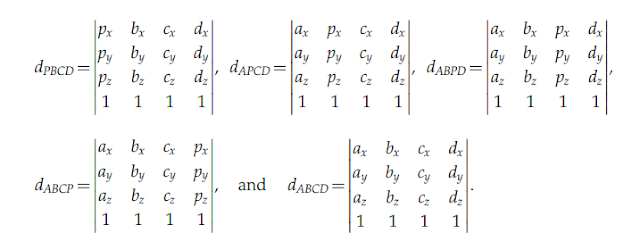
댓글 없음:
댓글 쓰기