4.1 The maximum-subarray problem
4.2 Strassen's algorithm for matrix multiplication
4.3 The substitution method for solving recurrences
4.4 The recursion-tree method for solving recurrences
4.5 The master method for solving recurrences
4.6 Proof of the master theorem
4 Divide-and-Conquer
In Section 2.3.1, we saw how merge sort serves as an example of the divide-and-conquer paradigm. Recall that in divide-and-conquer, we solve a problem recursively, applying three steps at each level of the recursion:
Divide the problem into a number of subproblems that are smaller instances of the same problem.
Conquer the subproblems by solving them recursively. If the subproblem sizes are small enough, however, just solve the subproblems in a straight forward manner.
Combine the solutions to the subproblems into the solution for the original problem.
When the subproblems are large enough to solve recursively, we call that the recursive case. Once the subproblems become small enough that we no longer recurse, we say that the recursion "bottoms out" and that we have gotten down to the base case. Sometimes, in addition to subproblems that are smaller instances of the same problem, we have to solve subproblems that are not quite the same as the original problem. We consider solving such subproblems as part of the combine step.
In this chapter, we shall see more algorithms based on divide-and-conquer. The first one solves the maximum-subarray problem: it takes as input an array of numbers, and it determines the contiguous subarray whose values have the greates sum. Then we shall see two divide-and-conquer algorithm for multiplying n x n matrices. One runs in Ө(n^3) time, which is no better than the straightforward method of multiplying square matrices. But the other, Strassen's algorithm runs in O(n^2.81) time, which beats the straightforward method asymptotically.
Recurrences
Recurrences go hand in hand with the divide-and-conquer paradigm, because they give us a natural way to characterize the running times of divide-and-conquer algorithms. A recurrence is an equation or inequality that describes a function in terms of its value on smaller inputs. For example, in Section 2.3.2 we described the worst-case running time T(n) of the MERGE-SORT procedure by the recurrence
whose solution we claimed to be T(n) = Ө(nlgn).
... This chapter offers three methods for solving recurrences - that is, for obtaining asymptotic "Ө" or "O" bounds on the solution:
- In the substitution method, we guess a bound and then use mathematical induction to prove our guess correct
- The recursion-tree method converts the recurrence into a tree whose nodes represent the costs incurred at various levels of the recursion. We use techniques for bounding summations to solve the recurrence.
- The master method provies bounds for recurrences of the form T(n) = aT(n/b) + f(n), (4.2) where a >= 1, b > 1, and f(n) is a given function. Such recurrences arise frequently. A recurrence of the form in equation 4.2 characterizes a divide-and-conquer algorithm that creates a subproblems, each of which is 1/b the size of the original problem, and in which the divide and combine steps together take f(n) time. To use the master method, you will need to memorize three cases, but once you do that, you will easily be able to determine asymptotic bounds for many simple recurrences. We will use the master method to determine the running times of the divide-and-conquer algorithms for the maximum-subarray problem and for matrix multiplication, as well as for other algorithms based on divide-and-conquer elsewhere in this book.
Technicalities in recurrences
In practice, we neglect certain technical details when we state and solve recurrences. For example, if we call MERGE-SORT on n elements when n is odd, we end up with subproblems of size floor(n/2) and ceiling(n/2). Neither size is actually n/2, because n/2 is not an integer when n is odd. Technically, the recurrence describing the worst-case running time of MERGE-SORT is rerally
T(n) = theta(1) if n = 1,
T(ceiling(n/2)) + T(floor(n/2)) + theta(n) if n > 1.
.. Consequently, for convenience, we shall generally omit statements of the boundary conditions of recurrences and assume that T(n) is contant for small n.
... In this chapter, however, we shall address some of these details and illustrate the fine points of recurrence solution methods.
4.1 The maximum-subarray problem
Suppose that you been offered the opportunity to invest in the Volatile Chemical Corporation. Like the chemicals the company produces, the stock price of the Volatile Chemical Corporation is rather volatile. You are allowed to buy one unit of stock only one time and then sell it at a later date, buying and selling after the close of trading for the day. To compensate for this restriction, you are allowed to learn what the price of the stock will be in the future. Your goal is to maximize your profit. Figure 4.1 shows the price of the stock over a 17-day period. You may buy the stock at any one time, starting after day 0, when the price is $100 per share. Of course, you would want to "buy low, sell high" - buy at the lowest possible price and later on sell at the highest possible price - to maximize your profit. Unfortunately, you might not be able to buy at the lowest price and then sell at the highest price within a given period. In Figure 4.1, the lowest price occurs after day 7, which occurs after the highest price, after day 1.
You might think that you can always maximize profit by either buying at the lowest price or selling at the highest price. For example, in Figure 4.1, we would maximize profit by buying at the lowest price, after day 7. If this strategy always worked, then it would be easy to determine how to maximize profit: find the highest and lowest prices, and then work left from the highest price to find the lowest prior price, work right from the lowest price to find the highest later price, and take the pair with the greater difference. Figure 4.2 shows a simple counterexample, demonstrating that the maxmimum profit sometimes comes neither by buying at the lowest price nor by selling at the highset price.
A brute-force solution
We can easily devise a brute-force solution to this problem: just try every possible pair of buy and sell dates in which the buy date precedes the sell date. A period of n days has  such pairs of dates. Since
such pairs of dates. Since  is Ө(n^2), and the best we can hope for is to evaluate each pair of dates in constant time, this approach would take Ω(n^2) time. Can we do better?
is Ө(n^2), and the best we can hope for is to evaluate each pair of dates in constant time, this approach would take Ω(n^2) time. Can we do better?
A transformation
In order to design an algorithm with an o(n^2) running time, we will look at the input in a slightly different way. We want to find a sequence of days over which the net change from the first day to the last is maximum. Instead of looking at the daily prices, let us instead consider the daily change in price, where the change on day i is the difference between the prices after day i - 1 and after day i. The table in Figure 4.1 shows these daily changes in the bottom row. If we treat this row as an array A, shown in Figure 4.3, we now want to find the nonempty, contiguous subarray of A whose values have the largest sum. We call this contiguous subarray the maximum subarray. For example, in the array of Figure 4.3, the maximum subarray of A[1..16] is A[8..11], with the sum 43. Thus, you would want to buy the stock just before day 8 (that is, after day 7) and sell it after day 11, earning a profit of $43 per share.
At first glane, this transformation does not help. We still need to check 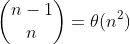
subarrays for a period of n days. Exercise 4.1-2 asks you to show that although computing the cost of one subarray might take time proportional to the length of the subarray, when computing all Ө(n^2) subarray sums, we can organize the computation so that each subarray sum takes O(1) time, given the values of previously computed subarray sums, so that the brute-forece solution takes Ө(n^2) time.
So let us seek a more efficient solution to the maximum-subarray problem. When doing so, we will usually speack of "a" maximum subarray rather than "the" maximum subarray, since there could be more than one subarray that achieves the maximum sum.
The maximum-subarray problem is interesting only when the array contains some negative numbers. If all the array entries were nonnegative, then the maximum-subaaray problem would present no challenge, since the entier array would give the greatest sum.
A solution using divide-and-conquer
Let's think about how we might solve the maximum-subarray problem using the divide-and-conquer technique. Suppose we want to find a maximum subarray of the subarray A[low..high]. Divide-and-conquer suggests that we divide the subarray into two subarrays of as equal size as possible. That is, we find the midpoint, say mid, of the subarray, and consider the subarrays A[low . . mid] and A[mid + 1 .. high]. As Figure 4.4(a) shows, any contiguous subarray A[i..j] of A[low.. high] must lie in exactly one of the following places:
- entirely in the subarray A[low..mid], so that low <= i <= j <= mid,
- entirely in the subarray A[mid + 1 . . high], so that mid < i <= j <= high, or
- crossing the midpoint, so that low <= i <= mid < j <= high.
Therefore, a maximum subarray of A[low.. high] must lie in exactly one of these places. In fact, a maximum subarray of A[low.. high] must have the greatest sum over all subarrays entirely in A[low.. mid], entirely in A[mid + 1.. high], or crossing the midpoint. We can find maximum subarrays of A[low..mid] and A[mid + 1..high] recursively, because these two subproblems are smaller instances of the problem of finding a maximum subarray. Thus, all that is left to do is find a maximum subarray that crosses the midpoint, and take a subarray with the largest sum of the three.
We can easily find a maximum subarray crossing the midpoint in time linear in the size of the subarray A[low..high]. This problem is not a smaller instance of our original problem, because it has the added restriction that the subarray it chooses must cross the midpoint. As Figure 4.4(b) shows, any subarray crossing the midpoint is itself made of two subarrays A[i .. mid] and A[mid + 1..j], where low<= i <= mid and mid < j <= high. Therefore, we just need to find maximum subarrays of the form A[i..mid] and A[mid + 1..j] and then combine them. The procedure FIND-MAX-CROSSING-SUBARRAY takes as input the array A and the indices low, mid, and high, and it returns a tuple containing the indices demarcating a maximum subarray that crosses the midpoint, along with the sum of values in a maximum subarray.
FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high) 1 left-sum = -infinity 2 sum = 0 3 for i = mid downto low 4 sum = sum + A[i] 5 if sum > left-sum 6 left-sum = sum 7 max-left = i 8 right-sum = -infinity 9 sum = 0 10 for j = mid + 1 to high 11 sum = sum + A[j] 12 if sum > right-sum 13 right-sum = sum 14 max-right = j 15 return (max-left, max-right, left-sum + right-sum)
This procedure works as follows. Lines 1-7 find a maximum subarray of the left half, A[low..mid]. Since this subarray must contain A[mid], the for loop of lines 3-7 starts the index i at mid and works down to low, so that every subarray it considers is of the form A[i..mid]. Lines 1-2 initialize the variables left-sum, which holds the greatest sum found so far, and sum, holding the sum of the entries in A[i..mid]. Whenever we find, in lin 5, a subarray A[i.. mid] with a sum of values greater than left-sum, we update left-sum to this subarray's sum in line 6, and in line 7 we update the variable max-left to record this index i. Lines 8-14 work analogously for the right half, A[mid + 1 ..high]. Here, the for loop of lines 10-14 starts the index j at mid + 1 and works up to high, so that every subarray it considers is of the form A[mid + 1..j]. Finally, line 15 returns the indices max-left and max-right that demarcate a maximum subarray crossing the midpoint, along with the sum left-sum + right-sum of the values in the subarray A[max-left..max-right].
If the subarray A[low.. high] contains n entries (so that n = high - low + 1), we claim that the call FIND-MAX-CROSSING-SUBARRAY(A,low, mid, high) takes Ө(n) time. Since each iteration of each of the two for loops takes Ө(1) time, we just need to count up how many iterations there are altogether The for loop of lines 3-7 makes mid - low + 1 iterations, and the for loop of lines 10-14 makes high - mid iterations,m, and so the total number of iterations is n.
With a linear-time FIND-MAX-CROSSING-SUBARRAY procedure in hand, we can write pseudocode for a divide-and-conquer algorithm to solve the maximum-subarray problem:
The initial call FIND-MAXIMUM-SUBARRAY(A, 1, A.length) will find a maximum subarray of A[1..n].
Similar to FIND-MAX-CROSSING-SUBARRAY, the recursive procedure FIND-MAXIMUM-SUBARRAY returns a tuple containing the indices that demarcate a maximum subarray, along with the sum of the values in a maximum subarray. Line 1 tests for the base case, where the subarray has just one element. A subarray with just one element has only one subarrray - itself - and so line 2 returns a tuple with the starting and ending indices of just the one element, along with its value. Lines 3 - 11 handle the recursive case. Line 3 does the divide part, computing the index mid of the midpoint. Let's refer to the subarray A[low..mid] as the left subarray and to A[mid+1..high] as the right subarray. Because we know that the subarray A[low..high] contains at least two elements, each of the left and right subarrays must have at least one element. Lines 4 and 5 conquer by recursively finding maximum subarrays within the left and right subarrays, respectively. Lines 6-11 form the combine part. Line 6 finds a maximum subarray that crosses the midpoint. (Recall that because line 6 solves a subproblem that is not a smaller instance of the original problem, we consider it to be in the combine part.) Line 7 tests whether the left subarray contains a subarray with the maximum sum, and line 8 returns that maximum subarray. Otherwise, line 9 test ~~
Analyzing the divide-and-conquer algorithm
Next we set up a recurrence that describes the running time of the recursive FIND-MAXIMUM-SUBARRAY procedure. As we did when we analyzed merge sort in Section 2.3.2, we make the simplifying assumption that the original problem size is a power of 2, so that all subproblem sizes are integers. We denote by T(n) the running time of FIND-MAXIMUM-SUBARRAY on a subarray of n elements. For starters, line 1 takes constant time. The base case, when n = 1, is easy: line 2 takes constant time, and so
T(1) = Ө(1)
The recursive case occurs when n > 1. Lines 1 and 3 take constant time. Each of the subproblems solved in lines 4 and 5 is on a subarray of n/2 elements (our assumption that the original problem size is a power of 2 ensures that n/2 is an integer), and so we spend T(n/2) time solving each of them. Because we have to solve two subproblems - for the left subarray and for the right subarray - the contribution to the running time from lines 4 and 5 comes to 2T(n/2). As we have already seen, the call to FIND-MAX-CROSSING-SUBARRAY in lines 6 takes Ө(n) time. Lines 7 - 11 take only Ө(1) time. For the recursive case, therefore, we have
T(n) = Ө(1) + 2T(n/2) + Ө(n) + Ө(1)
= 2T(n/2) + Ө(n)
Combining equations (4.5) and (4.6) gives us a recurrence for the running time T(n) of FIND-MAXIMUM-SUBARRAY:
T(n) = Ө(1) if n = 1,
2T(n/2) + Ө(n) if n > 1.
THis recurrence is the same as recurrence (4.1) for merge sort. As we shall see from the master method in Section 4.5, this recurrence has the solution T(n) = Ө(nlgn). YOu might also revisit the recursion tree in Figure 2.5 to understand why the solution should be T(n) = Ө(nlgn).
Thus, we see that the divide-and-conquer method yields an algorithm that is asymptotically faster than the brute-force method. With merge sort and now the maximum-subarray problem, we begin to get an idea of how powerful the divide-and-conquer method can be. Sometimes it will yield the asymptotically fastest algorithm for a problem, and other times we can do even better. As Exercise 4.1-5 shows, there is in fact a linear-time algorithm for the maximum-subarray problem, and it doest not use divide-and-conquer.
Exercises
4.1-1
What does FIND-MAXIMUM-SUBARRAY return when all elements of A are negative?
-> It will return the maximum value in the array. That is, the absolute value may be minimum in the array.
4.1-2
Write pesudocode for the brute-force method of solving the maximum-subarray problem. Your procedure should run in Ө(n^2) time.
4.1-3
Implement both the brute-force and recursive algorithms for the maximum-subarray problem on your own computer. What problem size n_0 gives the crossover point at which the recursive algorithm betas the brute-force algorithm? Then, change the base case of the recursive algorithm to use the brute-force algorithm whenever the problem size is less than n_0. Does that change the crossover point?
https://atekihcan.github.io/CLRS/E04.01-03/
I used this experiment data. So, the article said that the crossover will be around 17.
So..
4.1-4
Suppose we change the definition of the maximum-subarray problem to allow the result to be an empty subarray, where the sum of the values of an empty subarray is 0. How would you change any of the algorithms that do not allow empty subarrays to permit an empty subarray to be the result?
Instead of setting the left/right_sum -intmax, if we set set the left/right_sum 0, we can get 0.
4.1-5
Use the following ideas to develop a nonrecursive, linear-time algorithm for the maximum-subarray problem. Start at the left end of the array, and progress toward the right, keeping track of the maximum subarray seen so far. Knowing amaximum subarray of A[1..j], extend the answer to find a maximum subarray ending at index j + 1 by using the following observation : a maximum subarray of A [1.. j + 1] is either a maximum subarray of A[1..j] or a subarray A[i..j+1], for some 1 <= i <= j + 1. Determine a maximum subarray of the form A[i..j + 1] in constant time based on knowing a maximum subarray ending at index j.
4.2 Strassen's algorithm for matrix multiplication
... We must compute n^2 matrix entries, and each is the sum of n values. The following procedure takes n x n matrices A and B and multiplies them, returning their n x n product C. We assume that each matrix has an attribute rows, giving the number of rows in the matrix.
... Because each of the triply-nested for loops runs exactly n iterations, and each execution of line 7 takes constant time, the SQUARE-MATRIX-MULTIPLY procedure takes Ө(n^3) time.
You might at first think that any matrix multiplication algorithm must take Ω(n^3) time, since the natural definition of matrix multiplication requires that many multiplications. You would be incorrect, however: we have a way to multiply matrices in o(n^3) time. In this section, we shall see Strassen's remarkable recursive algorithm for multiplying n x n matrices. It runs in Ө(n^(lg7)) time, which we shall show in Section 4.5. Since lg7 lies between 280 and 2.81, Strassen's algorithm runs in O(n^2.81) time, which is asymptotically better that the simple SQUARE-MATRIX-MULTIPLY procedure
A simple divide-and-conquer algorithm
To keep things simple, when we use a divide-and-conquer algorithm to compute the matrix product C = A * B, we assume that n is an exact power of 2 in each of the n x n matrices. We make this assumption because in each divide step, we will divide n x n matrices into four n/2 x n/2 matrices, and by assuming that n is an exact power of 2, we are guaranteed that as long as n >= 2, the dimension n/2 is an integer.
...
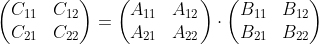
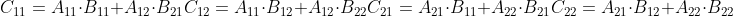
Each of these four equations specifies two multiplications of n/2 x n./2 matrices and the addition of their n/2 x n/2 products. We can use these equations to create a straightforward, recursive, and divide-and-conquer algorithm:
This pseudocdoe glosses over one subtle but important implementation detail. How do we partition the matrices in line 5? If we were to create 12 new n/2 x n/2 matrices, we would spend Ө(n^2) time copying entries. In fact, we can partition the matrices without copying entries. The trick is to use index calculations. We identify a submatrix by a range of row indices and a range of column indices of the original matrix. We end up representing a submatrix a little differently from how we represent the original matrix, which is the subtlety we are glossing over. The advantage is that, since we can specify submatrices by index calculations, excuting line 5 takes only Ө(1) time (although we shall see that it makes no difference asymptotically to the overall running time whether we copy or partition in place).
Now, we derive a reucrrence to characterize the running time of SQUARE-MATRIX-MULTIPLY-RECURSIVE. Let T(n) be the time to multiply two n x n matrices using this procedure. In the base case, when n = 1, we perform just the one scalar multiplication in line 4, and so
T(1) = Ө(1).
The recursive case occurs when n > 1. As discussed, partitioning the matrices in line 5 takes Ө(1) time, using index calculations. In lines 6-9, we recursively call SQUARE-MATRIX-MULTIPLY-RECURSIVE a total of eight times. Because each recursive call multiplies two n/2 x n/2 matrices, thereby contributing T(n/2) to the overall running time, the time taken by all eight recursive calls is 8T(n/2). We also must account for the four matrix additions in lines 6-9. Each of these matrices contains n^2/4 entries, and so each of the four matrix additions takes Ө(n^2) time. Since the number of matrix additions is a constant, the total time spent adding matrices in lines 6-9 is Ө(n^2). (Again, we use index calculations to place the results of the matrix additions into the correct positions of matrix C, with an overhead of Ө(1) time per entry.) The total time for the recursive case, therefore, is the sum of the partitioning time, the time for all the recursive calls, and the time to add the matrices resulting from the recursive calls:
T(n) = Ө(1) + 8T(n/2) + Ө(n^2)
= 8T(n/2) + Ө(n^2) (4.16)
Notice that if we implemented partitioning by copying matrices, which would cost Ө(n^2) time, the recurrence would not change, and hence the overall running time would increase by only a constant factor.
Combining equations (4.15) and (4.16) gives us the recurrence for the running time of SQUARE-MATRIX-MULTIPLY-RECURSIVE:
T(n) = Ө(1) if n = 1,
8T(n/2) + Ө(n^2) if n > 1.
As we shall see from the master method in Section 4.5, recurrence (4.17) has the solution T(n) = Ө(n^3). Thus, this simple divide-and-conquer approach is no faster than the straightforward SQUARE-MATRIX-MULTIPLY procedure.
Before we continue on to examining Strassen's algorithm, let us review where the components of equation (4.16) came from. Partitioning each n x n matrix by index calculation takes Ө(1) time, but we have two matrices to partition. Although you could say that partitioning the two matrices takes Ө(2) time, the constant of 2 is subsumed by the Ө-notation. Adding two matrices, each with, say, k entries, takes Ө(k) time. Since the matrices we add each have n^2/4 entries, you could say that adding each pair takes Ө(n^2/4) time. Again, however, the Ө-notation subsumes the contant factor of 1/4, and we say that adding two n^2/4 x n^2/4 matrices takes Ө(n^2) time. We have four such matrix additions, and once again, instead of saying that they take Ө(4n^2) time, we say that they take Ө(n^2) time. (Of course, you might observe that we could say that the four matrix additions take Ө(4n^2/4) time, and that 4n^2/4 = n^2, but the point here is that Ө-notation subsumes constant factors, whatever they are.) Thus, we end up with two terms of Ө(n^2), which we can combine into one.
When we account for the eight recursive calls, however, we cannot just subsume the constant factor of 8. In other words, we must say that together they take 8T(n/2) tme, rather than just T(n/2) time. You can get a feel for why by looking back at the recursion tree in Figure 2.5, for recurrence (2.1) (which is identical to recurrence(4.7)), with the recursive case T(n) = 2T(n/2) + Ө(n). The factor of 2 determined how many children each tree node had, which in turn determined how many terms contributed to the sum at each level of the tree. If we were to ignore the factor of 8 in equation (4.16) or the factor of 2 in recurrence (4.1), the recursion tree would just be linear, rather than "bushy," and each level would contribute only one term to the sum.
Bear in mind, therefore, that although asymptotic notation subsumes constant muliplicative factors, recursive notation such as T(n/2) does not.
Strassen's method
The key to Strassen's method is to make the recursion tree slightly less bushy. That is, instead of performing eight recursive multiplications of n/2 x n/2 matrices, it performs only seven. The cost of elminating one matrix multiplication will be several new additions of n/2 x n/2 matrices, but still only a constant number of additions. As before, the constant number of matrix additions will be subsumed by Ө-notation when we set up the recurrence equation to characterize the running time.
Strassen's method is not at all obvious. (This might be the biggest understatement in this book.) It has four steps:
We have traded off one matrix multiplication for a constant number of matrix additions. Once we understand recurrences and their solutions, we shall see that this tradeoff actually leads to a lower asymptotic running time. By the master method in Section 4.5, recurrence (4.18) has the solution T(n) = Ө(n^lg7).
We now proceed to describe the details. In step 2, we create the following 10 matrices:
S_1 = B_12 - B_22,
S_2 = A_11 + A_12,
S_3 = A_21 + A_22,
S_4 = B_21 - B_11,
S_5 = A_11 + A_22,
S_6 = B_11 + B_22
S_7 = A_12 - A_22,
S_8 = B_21 + B_22,
S_9 = A_11 - A_21,
S_10 = B_11 + B_12,
since we must add or subtract n/2 x n/2 matrices 10 times, this step does indeed take Ө(n^2) time.
In step 3, we recursively multiply n/2 x n/2 matrices seven times to compute the following n/2 x n/2 matrices, each of which is the sum or difference of proudcts of A and B submatrices:
P_1 = A_11 * S_1 = A_11 * B_12 - A_11 * B_22,
P_2 = S_2 * B_22 = A_11 * B_22 + A_12 * B_22,
P_3 = S_3 * B_11 = A_21 * B_11 + A_22 * B_11,
P_4 = A_22 * S_4 = A_22 * B_21 - A_22 * B_11,
P_5 = S_5 * S_7 = A_11 * B_11 + A_11 * B_22 + A_22 * B_11 + A_22 * B_22,
P_6 = S_7 * S_8 = A_12 * B_21 + A_12 * B_22 - A_22 * B_21 - A_22 * B_22,
P_7 = S_9 * S_19 = A_11 * B_11 + A_11 * B_12 - A_21 * B_21 - A_21 * B_12.
Note that only multiplications we need to perform are thos in the middle column of the above equations. The right-hand column just shows what these products equal in terms of the original submatrices created in step 1.
Step 4 adds and subtracts the P_i matrices created in step 3 to construct the four n/2 x n/2 submatrices of the product C. We start with
C_11 = P_5 + P_4 - P_2 + P_6,
Expending out the right-hand side, with the expansions of each P_i on its own line and vertically aligning terms that cancel out, we see that C_11 equlas
... A_11 * B_11 + A_12 * B_21.
which corresponds to equation (4.11).
Similarly, we set
C_12 = P_1 + P_2,
C_21 = P_3 + P_4
C_22 = P_5 + P_1 - P_3 - P_7.
.. Altogether, we add or subtract n/2 x n/2 matrices eight times in step 4, and so this step indeed takes Ө(n^2) time.
Thus, we see that Strassen's algorithm, comprising steps 1-4, produces the correct matrix product and that recurrence (4.18) characterizes its running time. Since we shall see in Section 4.5 that this recurrence has the solution T(n) = Ө(n^lg7), Strassen's method is asymptotically faster than the straightforward SQUARE-MATRIX-MULTIPLY procedure. The notes at the end of this chapter discuss some of the practical aspects of Strassen's algorithm.
Exercises
Note: Although Exercises 4.2-3, 4.2-4, and 4.2-5 are about variants on Strassen's algorithm, you should read Section 4.5 before trying to solve them.
4.2 - 1
Use Strassen's algorithm to compute the matrix product
4.2 - 2
Write pseudocode for Strassen's algorithm.
4.2 - 3
How would you modify Strassen's algorithm to multiply n x n matrices in which n is not an exact power of 2? Show that the resulting algorithm runs in time Ө(n^lg7).
4.2 - 4
What is the largest k such that if you can multiply 3 x 3 matrices using k multiplications (not assuming commutativity of multiplication), then you can multiply n x n matrices in time o(n^lg7)? What would the running time of this algorithm be?
4.2-5
V.Pan has discoverd a way of multiplying 68 x 68 matrices using 132,464 multiplications, a way of multiplying 70 x 70 matricies using 143,640 multiplications, and a way of multiplying 72 x 72 matrices using 155,424 multiplications. Which method yields the best asymptotic running time when used in a divide-and-conquer matrix-multiplication algorithm? How does it compare to Strassen's algorithm?
.... I do not want to figure our these exercises now.. I will do this later.
4.3 The substitution method for solving recurrences
Now that we have seen how recurrences characterize the running times of divide-and-conquer algorithms, we will learn how to solve recurrences. We start in this section with the "substitution" method.
The substitution method for solving recurrences comprises two steps:
If the subarray A[low.. high] contains n entries (so that n = high - low + 1), we claim that the call FIND-MAX-CROSSING-SUBARRAY(A,low, mid, high) takes Ө(n) time. Since each iteration of each of the two for loops takes Ө(1) time, we just need to count up how many iterations there are altogether The for loop of lines 3-7 makes mid - low + 1 iterations, and the for loop of lines 10-14 makes high - mid iterations,m, and so the total number of iterations is n.
With a linear-time FIND-MAX-CROSSING-SUBARRAY procedure in hand, we can write pseudocode for a divide-and-conquer algorithm to solve the maximum-subarray problem:
FIND-MAXIMUM-SUBARRAY(A,low, high) 1 if high == low 2 return (low, high, A[low]) // base case: only one element 3 else mid = floor((low+high)/2) 4 (left-low, left-high, left-sum) = FIND-MAXIMUM-SUBARRAY(A,low,mid) 5 (right-low, right-high, right-sum) = FIND-MAXIMUM-SUBARRAY(A, mid+1,high) 6 (cross-low, cross-high,cross-sum) = FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high) 7 if left-sum >= right-sum and left-sum >= cross-sum 8 return (left-low, left-high, left-sum) 9 else if right-sum>= left-sum and right-sum >=cross-sum 10 return (right-low, right-high, right-sum) 11 else return (cross-low, cross-high, cross-sum)
The initial call FIND-MAXIMUM-SUBARRAY(A, 1, A.length) will find a maximum subarray of A[1..n].
Similar to FIND-MAX-CROSSING-SUBARRAY, the recursive procedure FIND-MAXIMUM-SUBARRAY returns a tuple containing the indices that demarcate a maximum subarray, along with the sum of the values in a maximum subarray. Line 1 tests for the base case, where the subarray has just one element. A subarray with just one element has only one subarrray - itself - and so line 2 returns a tuple with the starting and ending indices of just the one element, along with its value. Lines 3 - 11 handle the recursive case. Line 3 does the divide part, computing the index mid of the midpoint. Let's refer to the subarray A[low..mid] as the left subarray and to A[mid+1..high] as the right subarray. Because we know that the subarray A[low..high] contains at least two elements, each of the left and right subarrays must have at least one element. Lines 4 and 5 conquer by recursively finding maximum subarrays within the left and right subarrays, respectively. Lines 6-11 form the combine part. Line 6 finds a maximum subarray that crosses the midpoint. (Recall that because line 6 solves a subproblem that is not a smaller instance of the original problem, we consider it to be in the combine part.) Line 7 tests whether the left subarray contains a subarray with the maximum sum, and line 8 returns that maximum subarray. Otherwise, line 9 test ~~
Analyzing the divide-and-conquer algorithm
Next we set up a recurrence that describes the running time of the recursive FIND-MAXIMUM-SUBARRAY procedure. As we did when we analyzed merge sort in Section 2.3.2, we make the simplifying assumption that the original problem size is a power of 2, so that all subproblem sizes are integers. We denote by T(n) the running time of FIND-MAXIMUM-SUBARRAY on a subarray of n elements. For starters, line 1 takes constant time. The base case, when n = 1, is easy: line 2 takes constant time, and so
T(1) = Ө(1)
The recursive case occurs when n > 1. Lines 1 and 3 take constant time. Each of the subproblems solved in lines 4 and 5 is on a subarray of n/2 elements (our assumption that the original problem size is a power of 2 ensures that n/2 is an integer), and so we spend T(n/2) time solving each of them. Because we have to solve two subproblems - for the left subarray and for the right subarray - the contribution to the running time from lines 4 and 5 comes to 2T(n/2). As we have already seen, the call to FIND-MAX-CROSSING-SUBARRAY in lines 6 takes Ө(n) time. Lines 7 - 11 take only Ө(1) time. For the recursive case, therefore, we have
T(n) = Ө(1) + 2T(n/2) + Ө(n) + Ө(1)
= 2T(n/2) + Ө(n)
Combining equations (4.5) and (4.6) gives us a recurrence for the running time T(n) of FIND-MAXIMUM-SUBARRAY:
T(n) = Ө(1) if n = 1,
2T(n/2) + Ө(n) if n > 1.
THis recurrence is the same as recurrence (4.1) for merge sort. As we shall see from the master method in Section 4.5, this recurrence has the solution T(n) = Ө(nlgn). YOu might also revisit the recursion tree in Figure 2.5 to understand why the solution should be T(n) = Ө(nlgn).
Thus, we see that the divide-and-conquer method yields an algorithm that is asymptotically faster than the brute-force method. With merge sort and now the maximum-subarray problem, we begin to get an idea of how powerful the divide-and-conquer method can be. Sometimes it will yield the asymptotically fastest algorithm for a problem, and other times we can do even better. As Exercise 4.1-5 shows, there is in fact a linear-time algorithm for the maximum-subarray problem, and it doest not use divide-and-conquer.
Exercises
4.1-1
What does FIND-MAXIMUM-SUBARRAY return when all elements of A are negative?
-> It will return the maximum value in the array. That is, the absolute value may be minimum in the array.
4.1-2
Write pesudocode for the brute-force method of solving the maximum-subarray problem. Your procedure should run in Ө(n^2) time.
pair<int,int> find_maximum_subarray() { int max = -intmax; int from, to; for(int i = 0; i < SIZE; ++i) { int sum = 0; for(int j = i; j < SIZE; ++j) { sum += testarr[j]; if (sum > max) { max = sum; from = i; to = j; } } } return mp(from, to); }
4.1-3
Implement both the brute-force and recursive algorithms for the maximum-subarray problem on your own computer. What problem size n_0 gives the crossover point at which the recursive algorithm betas the brute-force algorithm? Then, change the base case of the recursive algorithm to use the brute-force algorithm whenever the problem size is less than n_0. Does that change the crossover point?
https://atekihcan.github.io/CLRS/E04.01-03/
I used this experiment data. So, the article said that the crossover will be around 17.
So..
#define SIZE 1001 #define CROSSOVER 17 int number[SIZE]; struct info { int low; int high; int sum; }; info small_find_maximum_subarray(int low, int high) { int max = -intmax; int from, to; for(int i = low; i <= high; ++i) { int sum = 0; for(int j = i; j <= high ; ++j) { sum += number[j]; if (sum > max) { max = sum; from = i; to = j; } } } return { from, to, max }; } info find_max_crossing_subarray(int low, int mid, int high) { int left_sum = -intmax; int max_left = 0; int sum = 0; for (int i = mid; i >= low; --i) { sum += number[i]; if (sum > left_sum) { left_sum = sum; max_left = i; } } int right_sum = -intmax; int max_right = 0; sum = 0; for (int i = mid + 1; i <= high; ++i) { sum += number[i]; if (sum > right_sum) { right_sum = sum; max_right = i; } } return { max_left, max_right, left_sum + right_sum }; } info find_maximum_subarray(int low, int high) { if (high - low + 1 <= CROSSOVER) return small_find_maximum_subarray(low, high); else { int mid = floor((low + high) / 2); info left_sub = find_maximum_subarray(low, mid); info right_sub = find_maximum_subarray(mid + 1, high); info cross_sub = find_max_crossing_subarray(low, mid, high); if (left_sub.sum >= right_sub.sum && left_sub.sum >= cross_sub.sum) return left_sub; else if (right_sub.sum >= left_sub.sum && right_sub.sum >= cross_sub.sum) return right_sub; else return cross_sub; } }
4.1-4
Suppose we change the definition of the maximum-subarray problem to allow the result to be an empty subarray, where the sum of the values of an empty subarray is 0. How would you change any of the algorithms that do not allow empty subarrays to permit an empty subarray to be the result?
Instead of setting the left/right_sum -intmax, if we set set the left/right_sum 0, we can get 0.
4.1-5
Use the following ideas to develop a nonrecursive, linear-time algorithm for the maximum-subarray problem. Start at the left end of the array, and progress toward the right, keeping track of the maximum subarray seen so far. Knowing amaximum subarray of A[1..j], extend the answer to find a maximum subarray ending at index j + 1 by using the following observation : a maximum subarray of A [1.. j + 1] is either a maximum subarray of A[1..j] or a subarray A[i..j+1], for some 1 <= i <= j + 1. Determine a maximum subarray of the form A[i..j + 1] in constant time based on knowing a maximum subarray ending at index j.
struct info { int low; int high; int sum; }; info linear_find_maximum_subarray(int low, int high) { int from, to; int sum = number[low]; int temp_sum = number[low]; int temp_left = low; FOR(i, low + 1, high + 1) { temp_sum = number[i] > temp_sum + number[i] ? number[i] : temp_sum + number[i]; if (temp_sum > sum) { sum = temp_sum; to = i; from = temp_left; } if (temp_sum == number[i]) temp_left = i; } return {from, to, sum }; }
4.2 Strassen's algorithm for matrix multiplication
... We must compute n^2 matrix entries, and each is the sum of n values. The following procedure takes n x n matrices A and B and multiplies them, returning their n x n product C. We assume that each matrix has an attribute rows, giving the number of rows in the matrix.
SQUARE-MATRIX-MULTIPLY(A,B) 1 n = A.rows 2 let C = be a new n x n matrix 3 for i = 1 to n 4 for j = 1 to n 5 c_ij = 0 6 for k = 1 to n 7 c_ij = c_ij + a_ik * b_kj 8 return C
... Because each of the triply-nested for loops runs exactly n iterations, and each execution of line 7 takes constant time, the SQUARE-MATRIX-MULTIPLY procedure takes Ө(n^3) time.
You might at first think that any matrix multiplication algorithm must take Ω(n^3) time, since the natural definition of matrix multiplication requires that many multiplications. You would be incorrect, however: we have a way to multiply matrices in o(n^3) time. In this section, we shall see Strassen's remarkable recursive algorithm for multiplying n x n matrices. It runs in Ө(n^(lg7)) time, which we shall show in Section 4.5. Since lg7 lies between 280 and 2.81, Strassen's algorithm runs in O(n^2.81) time, which is asymptotically better that the simple SQUARE-MATRIX-MULTIPLY procedure
A simple divide-and-conquer algorithm
To keep things simple, when we use a divide-and-conquer algorithm to compute the matrix product C = A * B, we assume that n is an exact power of 2 in each of the n x n matrices. We make this assumption because in each divide step, we will divide n x n matrices into four n/2 x n/2 matrices, and by assuming that n is an exact power of 2, we are guaranteed that as long as n >= 2, the dimension n/2 is an integer.
...
Each of these four equations specifies two multiplications of n/2 x n./2 matrices and the addition of their n/2 x n/2 products. We can use these equations to create a straightforward, recursive, and divide-and-conquer algorithm:
SQUARE-MATRIX-MULTIPLY-RECURSIVE(A,B) 1 n = A.rows 2 let C be a new n x n matrix 3 if n == 1 4 c_11 = a_11 * b_11 5 else partition A,B, and C as in equations (4.9) 6 C11 = SQUARE-MATRIX_MULTIPLY_RECURSIVE(A_11,B_11) + SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_12,B_21) 7 C12 = SQUARE-MATRIX_MULTIPLY_RECURSIVE(A_11,B_12) + SQUARE-MATRIX_MULTIPLY_RECURSIVE(A_12,B_22) 8 C21 = SQUARE-MATRIX_MULTIPLY_RECURSIVE(A_21,B_11) + SQUARE-MATRIX_MULTIPLY_RECURSIVE(A_22,B_21) 9 C22 = SQUARE-MATRIX_MULTIPLY_RECURSIVE(A_21,B_12) + SQUARE-MATRIX_MULTIPLY_RECURSIVE(A_22,B_22) 10 return C
This pseudocdoe glosses over one subtle but important implementation detail. How do we partition the matrices in line 5? If we were to create 12 new n/2 x n/2 matrices, we would spend Ө(n^2) time copying entries. In fact, we can partition the matrices without copying entries. The trick is to use index calculations. We identify a submatrix by a range of row indices and a range of column indices of the original matrix. We end up representing a submatrix a little differently from how we represent the original matrix, which is the subtlety we are glossing over. The advantage is that, since we can specify submatrices by index calculations, excuting line 5 takes only Ө(1) time (although we shall see that it makes no difference asymptotically to the overall running time whether we copy or partition in place).
Now, we derive a reucrrence to characterize the running time of SQUARE-MATRIX-MULTIPLY-RECURSIVE. Let T(n) be the time to multiply two n x n matrices using this procedure. In the base case, when n = 1, we perform just the one scalar multiplication in line 4, and so
T(1) = Ө(1).
The recursive case occurs when n > 1. As discussed, partitioning the matrices in line 5 takes Ө(1) time, using index calculations. In lines 6-9, we recursively call SQUARE-MATRIX-MULTIPLY-RECURSIVE a total of eight times. Because each recursive call multiplies two n/2 x n/2 matrices, thereby contributing T(n/2) to the overall running time, the time taken by all eight recursive calls is 8T(n/2). We also must account for the four matrix additions in lines 6-9. Each of these matrices contains n^2/4 entries, and so each of the four matrix additions takes Ө(n^2) time. Since the number of matrix additions is a constant, the total time spent adding matrices in lines 6-9 is Ө(n^2). (Again, we use index calculations to place the results of the matrix additions into the correct positions of matrix C, with an overhead of Ө(1) time per entry.) The total time for the recursive case, therefore, is the sum of the partitioning time, the time for all the recursive calls, and the time to add the matrices resulting from the recursive calls:
T(n) = Ө(1) + 8T(n/2) + Ө(n^2)
= 8T(n/2) + Ө(n^2) (4.16)
Notice that if we implemented partitioning by copying matrices, which would cost Ө(n^2) time, the recurrence would not change, and hence the overall running time would increase by only a constant factor.
Combining equations (4.15) and (4.16) gives us the recurrence for the running time of SQUARE-MATRIX-MULTIPLY-RECURSIVE:
T(n) = Ө(1) if n = 1,
8T(n/2) + Ө(n^2) if n > 1.
As we shall see from the master method in Section 4.5, recurrence (4.17) has the solution T(n) = Ө(n^3). Thus, this simple divide-and-conquer approach is no faster than the straightforward SQUARE-MATRIX-MULTIPLY procedure.
Before we continue on to examining Strassen's algorithm, let us review where the components of equation (4.16) came from. Partitioning each n x n matrix by index calculation takes Ө(1) time, but we have two matrices to partition. Although you could say that partitioning the two matrices takes Ө(2) time, the constant of 2 is subsumed by the Ө-notation. Adding two matrices, each with, say, k entries, takes Ө(k) time. Since the matrices we add each have n^2/4 entries, you could say that adding each pair takes Ө(n^2/4) time. Again, however, the Ө-notation subsumes the contant factor of 1/4, and we say that adding two n^2/4 x n^2/4 matrices takes Ө(n^2) time. We have four such matrix additions, and once again, instead of saying that they take Ө(4n^2) time, we say that they take Ө(n^2) time. (Of course, you might observe that we could say that the four matrix additions take Ө(4n^2/4) time, and that 4n^2/4 = n^2, but the point here is that Ө-notation subsumes constant factors, whatever they are.) Thus, we end up with two terms of Ө(n^2), which we can combine into one.
When we account for the eight recursive calls, however, we cannot just subsume the constant factor of 8. In other words, we must say that together they take 8T(n/2) tme, rather than just T(n/2) time. You can get a feel for why by looking back at the recursion tree in Figure 2.5, for recurrence (2.1) (which is identical to recurrence(4.7)), with the recursive case T(n) = 2T(n/2) + Ө(n). The factor of 2 determined how many children each tree node had, which in turn determined how many terms contributed to the sum at each level of the tree. If we were to ignore the factor of 8 in equation (4.16) or the factor of 2 in recurrence (4.1), the recursion tree would just be linear, rather than "bushy," and each level would contribute only one term to the sum.
Bear in mind, therefore, that although asymptotic notation subsumes constant muliplicative factors, recursive notation such as T(n/2) does not.
Strassen's method
The key to Strassen's method is to make the recursion tree slightly less bushy. That is, instead of performing eight recursive multiplications of n/2 x n/2 matrices, it performs only seven. The cost of elminating one matrix multiplication will be several new additions of n/2 x n/2 matrices, but still only a constant number of additions. As before, the constant number of matrix additions will be subsumed by Ө-notation when we set up the recurrence equation to characterize the running time.
Strassen's method is not at all obvious. (This might be the biggest understatement in this book.) It has four steps:
- Divide the input matrices A and B and output matirx C into n/2 x n/2 submatrices, as in equation(4.9). This step takes Ө(1) time by index calculation, just as in SQUARE-MATRIX-MULTIPLY-RECURSIVE
- Create 10 matrices S_1, S_2, ..., S_10, each of which is n/2 X n/2 and is the sum or difference of two matrices created in step 1. We can create all 10 matrices in Ө(n^2) time.
- Using the submatrices created in step 1 and the 10 matrices created in step 2, recursively compute seven matrix products P_1, P_2, ... , P_7. Each matrix P_i is n/2 x n/2.
- Compute the desired submatrices C_11, C_12, C_21, C_22 of the result matrix C by adding and subtracting various combinations of the P_i matrices. We can compute all four submatrices in Ө(n^2) time.
We shall see the details of steps 2-4 in a moment, but we already have enough information to set up a recurrence for the running time of Strassen's method. Let us assume that once the matrix size n gets down to 1, we perform a simple scalar multiplication, just as in line 4 of SQURAE-MATRIX-MULTIPLY-RECURSIVE. When n > 1, steps 1, 2, and 4 take a total of Ө(n^2) time, and step 3 requires us to perform seven multiplications of n/2 x n/2 matrices. Hence, we obtain the following recurrence for the running time T(n) of Strassen's algorithm:
T(n) = Ө(1) if n = 1,
7T(n/2) + Ө(n^2) if n> 1.
We have traded off one matrix multiplication for a constant number of matrix additions. Once we understand recurrences and their solutions, we shall see that this tradeoff actually leads to a lower asymptotic running time. By the master method in Section 4.5, recurrence (4.18) has the solution T(n) = Ө(n^lg7).
We now proceed to describe the details. In step 2, we create the following 10 matrices:
S_1 = B_12 - B_22,
S_2 = A_11 + A_12,
S_3 = A_21 + A_22,
S_4 = B_21 - B_11,
S_5 = A_11 + A_22,
S_6 = B_11 + B_22
S_7 = A_12 - A_22,
S_8 = B_21 + B_22,
S_9 = A_11 - A_21,
S_10 = B_11 + B_12,
since we must add or subtract n/2 x n/2 matrices 10 times, this step does indeed take Ө(n^2) time.
In step 3, we recursively multiply n/2 x n/2 matrices seven times to compute the following n/2 x n/2 matrices, each of which is the sum or difference of proudcts of A and B submatrices:
P_1 = A_11 * S_1 = A_11 * B_12 - A_11 * B_22,
P_2 = S_2 * B_22 = A_11 * B_22 + A_12 * B_22,
P_3 = S_3 * B_11 = A_21 * B_11 + A_22 * B_11,
P_4 = A_22 * S_4 = A_22 * B_21 - A_22 * B_11,
P_5 = S_5 * S_7 = A_11 * B_11 + A_11 * B_22 + A_22 * B_11 + A_22 * B_22,
P_6 = S_7 * S_8 = A_12 * B_21 + A_12 * B_22 - A_22 * B_21 - A_22 * B_22,
P_7 = S_9 * S_19 = A_11 * B_11 + A_11 * B_12 - A_21 * B_21 - A_21 * B_12.
Note that only multiplications we need to perform are thos in the middle column of the above equations. The right-hand column just shows what these products equal in terms of the original submatrices created in step 1.
Step 4 adds and subtracts the P_i matrices created in step 3 to construct the four n/2 x n/2 submatrices of the product C. We start with
C_11 = P_5 + P_4 - P_2 + P_6,
Expending out the right-hand side, with the expansions of each P_i on its own line and vertically aligning terms that cancel out, we see that C_11 equlas
... A_11 * B_11 + A_12 * B_21.
which corresponds to equation (4.11).
Similarly, we set
C_12 = P_1 + P_2,
C_21 = P_3 + P_4
C_22 = P_5 + P_1 - P_3 - P_7.
.. Altogether, we add or subtract n/2 x n/2 matrices eight times in step 4, and so this step indeed takes Ө(n^2) time.
Thus, we see that Strassen's algorithm, comprising steps 1-4, produces the correct matrix product and that recurrence (4.18) characterizes its running time. Since we shall see in Section 4.5 that this recurrence has the solution T(n) = Ө(n^lg7), Strassen's method is asymptotically faster than the straightforward SQUARE-MATRIX-MULTIPLY procedure. The notes at the end of this chapter discuss some of the practical aspects of Strassen's algorithm.
Exercises
Note: Although Exercises 4.2-3, 4.2-4, and 4.2-5 are about variants on Strassen's algorithm, you should read Section 4.5 before trying to solve them.
4.2 - 1
Use Strassen's algorithm to compute the matrix product
4.2 - 2
Write pseudocode for Strassen's algorithm.
4.2 - 3
How would you modify Strassen's algorithm to multiply n x n matrices in which n is not an exact power of 2? Show that the resulting algorithm runs in time Ө(n^lg7).
4.2 - 4
What is the largest k such that if you can multiply 3 x 3 matrices using k multiplications (not assuming commutativity of multiplication), then you can multiply n x n matrices in time o(n^lg7)? What would the running time of this algorithm be?
4.2-5
V.Pan has discoverd a way of multiplying 68 x 68 matrices using 132,464 multiplications, a way of multiplying 70 x 70 matricies using 143,640 multiplications, and a way of multiplying 72 x 72 matrices using 155,424 multiplications. Which method yields the best asymptotic running time when used in a divide-and-conquer matrix-multiplication algorithm? How does it compare to Strassen's algorithm?
.... I do not want to figure our these exercises now.. I will do this later.
4.3 The substitution method for solving recurrences
Now that we have seen how recurrences characterize the running times of divide-and-conquer algorithms, we will learn how to solve recurrences. We start in this section with the "substitution" method.
The substitution method for solving recurrences comprises two steps:
- Guess the form of the solution.
- Use mathematical induction to find the constants and show that the solution works.
We substitute the guessed solution for the function when applying the inductive hypothesis to smaller values; hence the name "substitution method." This method is powerful, but we must be able to guess the form of the answer in order to apply it.
We can use the substitution method to establish either upper or lower bounds on a recurrence. As an example, let us determine an upper bound on the recurrence
T(n) = 2T(floor(n/2]) + n,
which is similar to recurrences (4.3) and (4.4). We guess that the solution is T(n) = O(nlgn). The substitution method requires us to prove that T(n) <= cnlgn for an appropriate choice of the constant c > 0. We start by assuming that this bound holds for all positive m < n, in particular for m = floor(n/2), yielding
T(floor(n/2)) <= cfloor(n/2) lg(floor(n/2)). Substituting into the recurrence yields
T(n) <= 2(cfloor(n/2) lg(floor(n/2))) + n
<= cnlg(n/2) + n
= cnlgn - cnlg2 + n
= cnlgn - cn + n
<= cnlgn,
where the last step holds as long as c >= 1.
4.3 ~~ 4.6 is for the more detailed technique of estimating the time complexity for an algorithm. I thinks it's too much for me now. So, I will just check the problems which may be helpful for me.
댓글 없음:
댓글 쓰기